Энтропия

Пример решения задачи

22. При нагревании двухатомного идеального газа ( 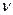= 2 моля) его термодинамическая температура увеличилась в 2 раза (n = 2). Определите изменение энтропии, если нагревание происходит: 1)изохорно; 2) изобарно.

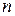Дано: i = 5 = 2,0 моля = 1) V = const 2) p = const	Решение 1)V = const. Из определения энтропии . Изменение энтропии , где – молярная теплоёмкость при постоянном давлении. Так как , то = 28,8 Дж/К 29 Дж/К
? ?

 

2) р = const.

Учитывая что , где – молярная теплоёмкость при постоянном давлении аналогично п. 1 получим:

= Дж/К.

Ответ: 1) 29 Дж/К; 2) Дж/К.

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

2.33. Какое количество тепла Q нужно сообщить 75 г водяных паров, чтобы нагреть их от 100 С до 250 °С при постоянном давлении? Определите изменение энтропии водяного пара.

(Q = 20,8 кДж; DS = 47,5 Дж/К)

2.34. Определить изменение DS энтропии при изотермическом расширении кислорода массой m = 10 г от объема V₁ = 25 л до объема V₂ = 100 л. (Относительная молекулярная масса кислорода 32).

(3,6 Дж/К)

2.35. Найти изменение DS энтропии при нагревании воды массой m = 100 г от температуры t₁ = 0 °C до температуры t₂ = 100 °C и последующим превращении воды в пар той же температуры. Удельная теплоемкость воды C = 4,18 кДж/(кг×К), удельная теплота парообразования воды 2,25×10³ кДж/кг.

(737Дж/К)

2.36. Найти изменение DS энтропии при превращении массы m = 200 г льда, находившегося при температуре t₁ = -10,7 °C в воду при t₂ = 0 °C.

Теплоемкость льда считать не зависящей от температуры. С = 2,1×10³ Дж/(кг×К). Температуру плавления принять равной 273 К.Удельная теплота плавления льда l = 333×10³ Дж/кг.

(DS = m[C×ln(T₂/T₁)+l/T₂] = 261 Дж/К)

2.37. Один киломоль газа изобарически нагревается от 20 до 600 °С, при этом газ поглощает 1,20×10⁷ Дж тепла. Найти число степеней свободы молекулы газа i; построить зависимость энтропии S как функцию от температуры Т газа.

(i = 3)