Выпуклость и вогнутость графика функции. Точки перегиба.
График дифференцируемой функции 
называется выпуклым (или выпуклым вниз) на интервале xÎ(a;b), если он расположен выше любой касательной, проведенной к графику на этом интервале.
График функции называется вогнутым (или выпуклым вверх) на интервале xÎ(a;b), если он расположен ниже любой касательной, проведенной к графику на этом интервале.
Точка графика непрерывной функции , отделяющая его выпуклую часть от вогнутой, называется точкой перегиба.
В простейших случаях область определения функции можно разбить на конечное число интервалов с постоянным направлением выпуклости.
При xÎ(a;х0) график вогнутый, при xÎ(х0;b) выпуклый, М0(х0;y0) – точка перегиба.
Достаточное условие выпуклости, вогнутости.
Если функция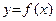 
является дважды дифференцируемой и ее 
сохраняет знак при всех xÎ(a;b), то график функции имеет постоянное направление выпуклости на этом интервале:
при <0 – выпуклость вверх (вогнутость),
при >0 – выпуклость вниз, или просто выпуклость.
Необходимое условие для точки перегиба.
Если x0 – абсцисса точки перегиба графика функции , то 
или 
не существует.
Необходимое условие не является достаточным. Точки, принадлежащие графику функции , в которых или не существует, называются подозрительными на перегиб.
Достаточное условие для точек перегиба.
Если вторая производная при переходе через точку х0, подозрительную на перегиб, изменяет знак, то точка графика с абсциссой х0 является точкой перегиба. Если не изменяет знак при переходе через точку х0, то перегиба нет.
В следующих примерах требуется определить точки перегиба и интервалы выпуклости и вогнутости графиков функций.
Пример 1.
.
Решение.
Область определения функции 
.
Находим 
;
.
при х1 = 0, х2 = 1, х3 = 3 – это точки, подозрительные на перегиб.
Проверяем достаточное условие выпуклости, вогнутости, точек перегиба:
При х = 1 и х = 3 есть перегибы, при х = 0 перегиба нет.
Вычисляем ординаты точек перегиба:
; 
.
Ответ: точки перегиба М1(1; 5,5) и М2(3; –112,5),
график выпуклый при xÎ(–¥; 1) и xÎ(3; +¥), график вогнутый при xÎ(1; 3).
Пример 2.
.
Решение.
Область определения функции: xÎ(–¥;+¥).
Находим 
, 
.
не существует при х=0, но изменяет знак с ²+² на ²–² при переходе через х=0. Поэтому точка графика (0;0) является точкой перегиба, при xÎ(–¥;0) график выпуклый, при xÎ(0;+¥) – вогнутый.
Дополнительные упражнения.
Определить интервалы выпуклости и вогнутости графиков следующих функций. Найти точки перегибов.
| 1. y=3x4–8x3+6x2+12; |
| 2. y=x3–12x2+x–1; |
| 3. y=ln(1+x2); |
4. y=  ;
|
5.  .
|
Ответы.
1. Точки перегиба 
и 
;
при 
и 
график вогнутый,
при 
график выпуклый.
2. Точка перегиба 
;
при 
график вогнутый,
при 
график выпуклый.
3. Точка перегиба 
и 
;
при 
и график вогнутый,
при 
график выпуклый.
4. Точка перегиба 
и 
;
при 
и 
график выпуклый,
при 
график вогнутый.
5. Точка перегиба 
;
при 
график вогнутый,
при 
график выпуклый.