Обратные тригонометрические функции, их свойства и графики.

Функция арксинус y = arcsin(x).

 

Изобразим график функции арксинус:

 

Свойства функции арксинус y = arcsin(x):

1.Областью определения: .

2.Область значений: .

3.Функция арксинус - нечетная.

4.Функция арксинус возрастает при .

5.Функция вогнутая при , выпуклая при .

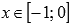6.Точка перегиба (0; 0), она же ноль функции.

7.Асимптот нет.

 

Функция арккосинус y = arccos(x).

График функции арккосинус имеет вид:

Свойства функции арккосинус y = arccos(x):

1.Область определения: .

2.Область значений: .

3.Функция не является ни четной ни нечетной.

4.Функция арккосинус убывает при .

5.Функция вогнутая при 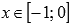, выпуклая при .

6.Точка перегиба .

7.Асимптот нет.

Функция арктангенс y = arctg(x).

 

График функции арктангенс имеет вид:

 

 

Свойства функции арктангенс y = arctg(x):

1.Область определения: .

2.Область значений: .

3.Функция арктангенс - нечетная.

4.Функция возрастает при .

5.Функция арктангенс вогнутая при , выпуклая при .

6.Точка перегиба (0; 0), она же ноль функции.

7.Горизонтальными асимптотами являются прямые при и при .

 

 

Функция арккотангенс y = arcctg(x).

 

Изобразим график функции арккотангенс:

 

 

Свойства функции арккотангенс y = arcctg(x):

1.Областью определения: .

2.Область значений: .

3.Функция арккотангенс не является ни четной ни нечетной.

4.Функция убывает при .

5.Функция вогнутая при , выпуклая при .

6.Точка перегиба .

7.Горизонтальными асимптотами являются прямые при и y = 0 при .