Вычисление площадей плоских фигур
Пусть функция y=f(x) неотрицательна и непрерывна на отрезке [a, b]. Тогда по геометрическому смыслу определенного интеграла площадь S под кривой y=f(x) на [ a, b] численно равна определенному интегралу  , т.е.
, т.е.
S=  .
.
Пример. Найти площадь фигуры, ограниченной линиями 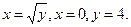
S = 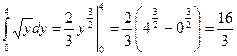 (кв. ед.)
(кв. ед.)
Пусть функция y=f(x) неположительна и непрерывна на отрезке [a, b]. Площадь S над кривой y=f(x) на [ a, b] отличается знаком от определенного интеграла  , т.е.
, т.е.
S= -  . (17)
. (17)
Приведем формулу, применение которой упрощает решение задач на вычисление площадей плоских фигур.
Теорема. Пусть на отрезке [a, b] заданы непрерывные функции y=f1(x) и y=f2(x) такие, что 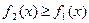 . Тогда площадь S фигуры, заключенной между кривыми y=f1(x) и y=f2(x) на отрезке [ a, b] вычисляется по формуле
. Тогда площадь S фигуры, заключенной между кривыми y=f1(x) и y=f2(x) на отрезке [ a, b] вычисляется по формуле
S=  . (18)
. (18)
Пример. Вычислить площадь фигуры, ограниченной линиями 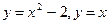
Найдем координаты точек пересечения параболы  и прямой
и прямой 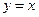 , решив систему этих уравнений: (-1; -1) и (2; 2). На отрезке [-1; 2]
, решив систему этих уравнений: (-1; -1) и (2; 2). На отрезке [-1; 2] 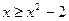 . Воспользуемся формулой (18), полагая f2(x)=x, f1(x)=x2 – 2. Абсциссы точек пересечения линий зададут пределы интегрирования:
. Воспользуемся формулой (18), полагая f2(x)=x, f1(x)=x2 – 2. Абсциссы точек пересечения линий зададут пределы интегрирования:
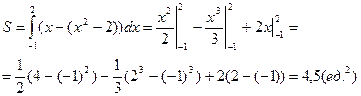
 |
Площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах уравнением r=f(
 ) и двумя лучами
) и двумя лучами 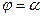 и
и  вычисляется по формуле:
вычисляется по формуле:

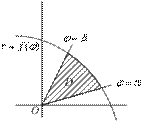
Пример. Найдём площадь 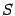 области, ограниченной частью спирали r=a
области, ограниченной частью спирали r=a 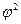 (a>0) при
(a>0) при 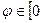 ;
;  и отрезком
и отрезком  ;
; 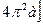 оси
оси  (см. рис.).
(см. рис.).
 |
Применяя формулу, получаем:
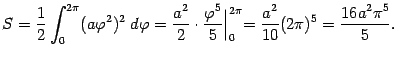
Если область 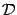 имеет границу, состоящую из двух отрезков лучей
имеет границу, состоящую из двух отрезков лучей 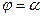 и
и  (эти отрезки могут вырождаться в одну точку) и двумя линиями, заданными уравнениями в полярных координатах: r=f1(
(эти отрезки могут вырождаться в одну точку) и двумя линиями, заданными уравнениями в полярных координатах: r=f1(  ) и r=f2(
) и r=f2(  ), причём f1(
), причём f1( 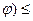 f2(
f2(  ), при всех
), при всех 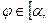
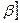 (см.рис.)
(см.рис.)
 |
то площадь
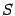 области
области 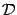 можно представить как разность двух площадей: S2— площади области, лежащей между лучами
можно представить как разность двух площадей: S2— площади области, лежащей между лучами 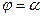 и
и  , и линией r=f2(
, и линией r=f2(  ), и S1— площади области, лежащей между лучами
), и S1— площади области, лежащей между лучами 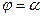 и
и  , линией r=f1(
, линией r=f1(  ).
).
Каждую из площадей S1 и S2 можно подсчитать по формуле, так что получаем в итоге
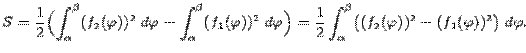
Если кривая задана параметрическими уравнениями x=x=(t) и y=y(t), то площадь криволинейной трапеции, ограниченной этой кривой, прямыми x=a, x=b и отрезком [a,b] оси Ox выражается формулой
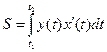 .
.