Интеграл с переменным верхним пределом интегрирования. Формула Ньютона-Лейбница

Если функция y=f(x) интегрируема на отрезке [a, b],то, очевидно, она интегрируема также на произвольном отрезке [a, х], вложенном в [a, b].

Положим по определению

Ф(х) = 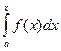= 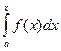, (9)

где [a, b], а функция Ф(х) называется интегралом с переменным верхнимпределом.

 

Свойства функции Ф(х) (интеграла с переменным верхним пределом):

 

Теорема 1. Если функция f(x) непрерывна на отрезке[a, b], то функция Ф(х) так же непрерывна на [a, b].

 

Теорема 2. Пусть функция f(x) непрерывна на отрезке[a, b]. Тогда в каждой точке х отрезка[a, b] производная функции Ф(х) по переменному пределу равна подынтегральной функции f(x), т.е.

Ф^’(х) = ( 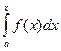)^’ = f(x).

Следствие. Если функция у = f(x) непрерывна на отрезке[a, b], то для этой функции существует первообразная на отрезке[a, b].