Свойства определенного интеграла
1. Постоянный множитель можно выносить за знак интеграла, т.е.
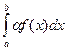 =
= 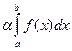 , (3)
, (3)
где 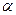 — некоторое число.
— некоторое число.
2. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, т.е.
 =
= 
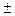
 (4)
(4)
3. Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей, т.е. при любых a, b, c:
 =
=  +
+  . (5)
. (5)
4. Если на отрезке [a, b], где a<b, f(x)  g(x), то и
g(x), то и 

 , т.е. обе части неравенства можно почленно интегрировать.
, т.е. обе части неравенства можно почленно интегрировать.
5.  = -
= - 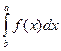 (6)
(6)
6. Теорема о среднем. Если функция y=f(x) непрерывна на отрезке [a, b], (где a<b), то найдется такое значение  [a, b], что
[a, b], что
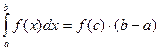 . (7)
. (7)
Свойство 6 (теорема о среднем) при f(x) 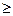 0 имеет простой геометрический смысл: значение определенного интеграла равно, при некотором
0 имеет простой геометрический смысл: значение определенного интеграла равно, при некотором  (a, b), площади прямоугольника с высотой f(c) и основанием b-a. Число
(a, b), площади прямоугольника с высотой f(c) и основанием b-a. Число
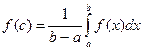 (8)
(8)
называется средним значением функции f(x) на отрезке [a, b].