Магнитного моментов субатомных частиц и фотона

В 1925 г. Г.Е.Уленбек и С.А. Гаудсмит открыли [66], что электрон обладает свойствами, соответствующими наличию у него спина (момента количества движения), величина которого одинакова для всех электронов. Экспериментальные данные позволяют подтвердить наличие спина электрона не только спектроскопически, но и посредством исследования траекторий электронов, движущихся с большой скоростью в неоднородном магнитном поле. Таким значительным экспериментом является опыт Штерна - Герлаха, который выполнен еще в 1921 году [67].

В этом эксперименте пучок серебра, выходивший через калиброванное отверстие, попадал в сильно неоднородное магнитное поле, создаваемое полюсами магнита специальной формы. Затем пучки, отклоненные полем, попадали на фотопластинку, и их следы удалось обнаружить после проявления пластинки. Установлено, что исходный пучок серебра расщеплялся на два пучка. На-

блюдаемое явление объяснялось при допущении, что атом серебра из-за наличия одного внешнего электрона обладает магнитным моментом, так как магнитный момент может быть ориентирован в одном из двух возможных направлений относительно силовых линий магнитного поля, а градиент магнитного поля создает силу, отклоняющую эти атомы вправо и влево.

Нынешняя физика так и не могла дать физического объяснения спина электрона и его магнитного момента, ибо не отражает реальной действительности мира. Поэтому Т. Эрдеи-Груз объективно отразил сложившуюся в науке ситуацию [67]:

«Спин следует рассматривать как некое фундаментальное свойство электрона, которое при современном уровне наших знаний нельзя объяснить на основе других явлений». Однако фрактальная физика позволяет разрешить данную проблему [5] и показать, что природа проста и едина.

В п. 4.1 и [7] представлена фрактальная форма субатомных частиц на основе анализа постоянной тонкой

структуры α^-1 = 137,03597. Субатомные частицы представляют собой форму полушара и показаны на рис. 4.1. Установление фрактальной формы частиц и фотона определило создание новой науки о природе, что позволяет объяснить проявляемые свойства электрона при его движении в неоднородном поле (показано на рис. 4.5).

Рис. 4.5. Графическое изображение эффекта расщепления пучка электронов на две составляющие:

а - наличие электронного спина можно обнаружить в неравномерном магнитном поле; б - объяснение притяжения одного пучка электронов накладываемым магнитным полем и отталкивания другого пучка тем же внешним магнитным полем; в - проекции формы электрона на координатные плоскости.

Расщепление пучка электронов на две составляющие можно объяснить, как сепарацию частиц по ориентации их формы (см. рис. 4.5а,б): в одной составляющей электроны ориентированы «полюсами», а в другой — электроны движутся своими «основаниями». При движении электронов в магнитном поле В влияние поля сводится к действию силы F_л Лоренца, приложенной в точке с радиус-вектором. Положение этой точки всецело определяется свойством самой формы электрона и совпадает с центром инерции частицы. Так как ориентация электро-нов разная, то и возникающий механический угловой (вращательный) момент (вследствие действия силы Лоренца на центры инерции частиц) имеет противоположные направления. При этом собственный механический момент (спин) электрона обусловливает возникновение магнитного момента. Вектор магнитного момента электрона антипараллелен вектору его собственного момента количества движения (спина). Причиной противоположных направлений моментов является отрицательный знак электрического заряда электрона. Следовательно, накладываемое магнитное поле притягивает один пучок, а другой пучок (другую составляющую исходного пучка) соответственно отталкивает с той же силой вследствие взаимодействия внешнего поля с магнитными полями электронов.

Для выявления свойств электрона дадим пояснение термина «магнитный момент». Из классической физики известно [68], что если ток идет по проводнику, замкнутому в кольцо, то возникающее магнитное поле аналогично соответствующему полю небольшого магнита, что то же — магнитного диполя. Величина магнитного мо-

мента такого замкнутого плоского контура с током равна току, умноженному на площадь, охватываемую этим контуром. Направление магнитного момента указывается по нормали к плоскости контура (кольца) так, чтобы из конца вектора ток оказался протекающим против часовой стрелки. Электроны и другие элементарные частицы, многие ядра, а также многочисленные атомы и ионы ведут себя как магнитные диполи. Величиной, характеризующей магнитный диполь, является магнитный момент. Это число характеризует отклик частицы на внешнее магнитное поле. Исходя из представлений фрактальной физики (см. п. 3.3), магнитное поле частицы возникает вследствие поляризации структуры пространства движущимся электроном. При этом момент количества движения (употребляются также названия вращательный или угловой момент) электрона есть произведение радиус-вектора вращения частицы на вектор ее количества движения.

Связь в системе СИ между магнитным моментом т, связанным с движением электронов в неоднородном магнитном поле, и собственным угловым (вращательным) моментом s электрона определяется с помощью гиромагнитного отношения γ, которое выражает отношение величины магнитного момента к механическому:

m = - γħs / ħ = - 2eħs/(m_e ħ) (4.14)

где m_е — масса электрона; -е — электрический заряд электрона; ħ = h/2 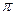— постоянная Планка. Единица, в которой выражена величина ħ, имеет размерность энергии, умноженной на время, что соответствует размерности момента количества движения. Величина с такой размерностью называется действием и постоянную Планка называют также элементарным квантом действия (см. п. 1.4). Для электрона, движущегося в неоднородном магнитном поле, в системе СИ значение = -2е/m_e = 3,518 • 10¹¹ А • с • кг^-1.

Для доказательства используем известные соотношения для движения твердого тела, хотя уже знаем (см. п. 4.1), что субатомные частицы не точки и не твердые полушарики, их следует рассматривать как электромагнитные волновые сгустки, несущие электрический заряд. Поэтому момент количества движения электрона, вращающегося с мгновенной угловой скоростью со (радианы в секунду) вокруг оси, проходящей через центр инерции электрона (центр расположен на оси симметрии на расстоянии 3/8 радиуса r полушара), равен I , где I — момент инерции, равный сумме произведений масс частиц тела на квадраты их расстояний до данной оси вращения. Тогда момент количества движения электрона запишем в виде:

(4.15)

где коэффициент 2 в знаменателе обусловлен точеч-ностью исследуемого объекта, к которому приложена сила в точке с радиус-вектором.

Так как заряд -еэлектрона имеет те же формы, что и масса m_e, то вызываемое аналогичное движение заряда электрона обусловливает возникновение магнитного момента. Поэтому, в соответствии с (4.14) и (4.15), магнитный момент электрона m представим как:

m = - I_e • = - 0,26er² = - 2es/m_е. (4.16)

Итак, убеждаемся в том, что полученное соотношение (4.16) равно (4.14).

На рис. 4.5в дано поясняющее представление формы электрона и его проекций на координатные плоскости: (1/2; 1/2; 1). Так как эксперименты по выявлению свойств электрона позволяют предположить возможность квантования момента количества движения в единицах h и соответственно записать собственный момент количества движения (спина) электрона как:

(4.17)

В (4.17) квантовое число под корнем 1/2(1/2 + 1) представляет собой связь проекций формы электрона, выражающая объем частицы (локальную фрактальную размерность) и, следовательно, определяет энергию взаимодействия частицы с внешним полем. Это обусловило для определения собственного момента количества движения электрона введение квадратного корня.

Спиновый магнитный момент в соответствии с (4.14) и (4.17) запишем в виде:

(4.18)

Однако специалисты в области ядерной физики, как правило, используют величину максимального значения составляющей магнитного момента частиц на направление поля z. Это направление поля z характеризует плоскость, проекцией частицы на которую является полукруг. Исходя из этого положения и соотношения (4.17), проекция собственного момента количества движения на направление поля z:

(s)_z = 1/2 ħ. (4.19)

Тогда в соответствии с экспериментом Штерна -Герлаха (описан в этом параграфе, см. выше) и соотношением (4.18) магнитный момент электрона на направление поля z равен:

(4.20)

Коэффициент 1/2 в соотношении (4.19) называют квантовым числом спинового момента электрона. Установление формы электрона в виде полушара (см. пп. 2.2, 2.8, 4.1) показывает корректное понимание величины 1/2 спина электрона, как представление проекции электрона на плоскости в виде половины круга. Поясним, что размерности проекций форм электрона и фотона определяют спины этих частиц, их следует понимать также в топологическом смысле, как число оборотов кривой вокруг своего центра вращения. Это число называется поряд-

ком кривой. Проекция фотона в форме восьмерки совершает вокруг своего центра один оборот, поэтому порядок имеет 1. В случае электрона порядок кривой составляет 1/2, ибо совершает вокруг своего центра только пол-оборота (см. таблицу физических объектов п. 2.8). Поэтому значение ±1/2 есть значения квантового числа, характеризующего проекции движущихся электронов на направление магнитного поля, что можно увидеть из рис. 4.5 б. Такое объяснение квантового числа спинового момента электрона также приводит к пересмотру абстрактного принципа Паули [54, 67].

Согласно принципу Паули в любом атоме в основном (невозбужденном) состоянии могут находиться только два электрона с противоположными спинами. Теперь принцип Паули можно сформулировать с позиции фрактальной физики, придав абстрактному представлению физическую сущность. Из фрактальной модели атома водорода (см. п. 4.2), показанной на рис. 4.4, известно [2], что электрон, имеющий отрицательный заряд, занимает определенное энергетическое положение, определяемое как притяжением глобальным зарядом протона q = +1, так и отталкиванием электрона, вызываемым локальным зарядом (кварком) протона (-1/3). Для обеспечения устойчивого энергетического положения протон водорода вращается вокруг центральной оси. Это вращение не позволяет происходить процессу захвата электрона положительными зарядами (кварками) протона. Тогда в основном состоянии (в отсутствии внешних возбуждений) в любом атоме вследствие действия кулоновских сил отталкивания, вызванных как действием отрицательных зарядов (кварков) нейтронной оболочки вращающегося ядра, так и взаимным влиянием электронов, два электрона располагаются в пространстве своими «основаниями» за счет притяжения глобального положительного заряда ядра так, что ориентация их формы оказывается противоположной. Следует заметить, вращение (спин) ядра вызывает собственный магнитный

момент, который также влияет на энергетическое положение электронной пары, ибо она (пара электронов) обладает спиновым магнитным моментом. Фрактальное представление этого свойства атома изображено на рис. 4.6.

Рис. 4.6. Расположение двух электронов в основном состоянии атома

Коэффициент 1 в соотношении (4.20) называют квантовым числом магнитного момента электрона, которое характеризует отклик частицы на внешнее магнитное поле. На основании изложенного можем сделать вывод, что квантовое число 1 есть значение проекции формы кванта электромагнитного поля, которое возникает вследствие поляризации структуры пространства движущейся частицей. Объяснение спина кванта электромагнитного поля — фотона представлено также в п. 4.1. Различие спинов фотона и электрона вызывается различием их форм, показанных на рис. 4.1. Поэтому возникающее магнитное поле движущегося электрона в форме замкнутых силовых линий характеризуется целым квантовым числом и пропорционально элементарному кванту действия ħ — постоянной Планка. Магнитный момент электрона в системе СИ выражается атомной единицей β_е = — e ħ /m_e, величина которой равна β_е = 1,855 • 10 ^-23 А • м².

Нынешняя физика использует другую несуществующую в природе связь — между магнитным моментом, связанным с вращением электронов по орбите, и орби-

тальным моментом электрона — с помощью магнетона Бора [68]. Однако при изучении всех элементов периодической таблицы (см. пп. 4.2, 4.4) установлено, что электроны не обращаются вокруг ядра, а занимают определенное энергетическое положение. Поэтому нынешняя физика использует неверное представление магнитного момента; чтобы связать это с экспериментом, она использует чистую спекуляцию [66]: «Этот факт учитывается, когда говорят, что необходимо ввести фактор 2 (называемый g-фактором для спина). Такой g-фактор 2 для спина электрона необходимо ввести в соответствии с теорией относительности».

Исходя из рис. 4.1, спин имеется у протона, причем квантовое число спина s = 1/2. Направление магнитного момента протона совпадает с направлением спина. С учетом строения протона и в соответствии с (4.18) запишем магнитный момент протона в виде:

Тогда магнитный момент протона в направлении поля z можно записать как:

где еħ/m_р — ядерный магнетон, который обозначили как β_я. Ядерный магнетон в системе СИ β_я = 1,010 ^. 10^-26А • м² дается тем же соотношением (4.20) при подстановке в него значения массы протона m_p. Так как магнитный момент протона по величине примерно в 658 раз меньше магнитного момента электрона, то его влияние чрезвычайно мало.

Квантовое число спина нейтрона также s = 1/2. Направление магнитного момента противоположно направлению спина. В соответствии с (4.22) магнитный момент нейтрона на направление поля z представим как:

(4.23)

Мы уже знаем (см. п. 4.1), что нынешняя физика не в состоянии объяснить структуру субатомных частиц и построить точную количественную теорию магнитных моментов нуклонов, так как магнитные моменты протона и нейтрона определяются структурной формой кварков. Структурное представление противоречит вероятностным формам изображения материи. Для определения магнитных моментов частиц сначала обратим внимание на вычисление локальных фрактальных размерностей упорядоченных пар зарядов (кварков) для протона и нейтрона (см. п. 2.2).

Локальная фрактальная размерность для протона составляет D_Lp = 10 + 2π/3 = 12,0944, а для нейтрона — d_L_n = 10 — π/4 = 9,2146. Эти результаты связаны с геометрией нуклонов.

Кварк протона зарядом (-1/3) (см. рис. 4.1) представляет собой тончайший слой, разделяющий частицу на две равные части — кварки зарядом ( + 2/3). Поэтому при вычислении локальной размерности протона определено слагаемое 2 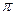/3 с учетом особенности этого слоя, мера которого на основании формулы среднего значения [36, 37] есть произведение 2 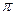— длины кривой (окружности), ограничивающей этот слой, — на значение заряда 1/3.

Два кварка нейтрона зарядом (-1/3) имеют форму сферического двуугольника со значением внутреннего угла π/4. Поэтому при определении размерности нейтрона это значение угла также учтено как отрицательное значение квазиобъема (см. п. 2.2 и [40]).

Размерность протона и нейтрона определялась с учетом свойства аддитивности меры. Значение 10 выявлено [34] как произведение линейных размерностей пространств пары кварков, для каждого из которых размерность (число координат) Е = 3. Пара кварков имеет общую прямую размерностью Е = 1.

Величина магнитного момента протона определена с помощью следующего соотношения:

М_р = Г(1/3) + 2Г(2/3)/(2 • 12,0944) = Г(1/3) +
Г(2/3)/12,0944 = 2,79. (4.24)

Величина магнитного момента нейтрона определяется как:

М_n = Г(2/3) + 2Г( 1/3)/9,2146 = 1,93. (4.25)

Выражение для значения магнитного момента электрона запишем в виде:

М_е = Г(1) + 0 = 1,00. (4.26)

Заметим, что соотношения (4.24), (4.25) и (4.26) есть соответственно выражения (4.4), (4.5) и (4.6). Повторение этих выражений сделано с целью дальнейшего разъяснения свойств субатомных частиц.

Магнитный момент нейтрона М_n и магнитный момент протона М_р выражены в новых ядерных магнетонах β_я. Магнитный момент электрона М_е выражен в новой атомной единице магнитного момента β_е. Г(z) — гамма-функция [34], которая выявлена при описании взаимодействия двух электронов (см. пп. 2.2, 4.1). В (4.24) и (4,25) ее значения Г(1/3) = 2,6789, Г(2/3) = 1,3541 [62]. Заметим, что при вычислении магнитного момента протона в (4.24) перед размерностью частицы 12,0944 стоял множитель 2 из-за наличия дельта - функции, вызываемой особенностью тончайшего слоя протона. Однако этот множитель сокращен с таким же множителем в числителе выражения (4.24) магнитного момента протона. Множитель 2 числителя (4.24) определял число кварков зарядом ( + 2/3). Второй член магнитных моментов (4.24) и (4.25) определен, исходя из фрактального (неклассического) представления производной (4.2), где изменяющаяся функция зарядов делится на локальную фрактальную размерность (квазиобъем) этих зарядов. В соотношении (4.26) изменение функции равно нулю, ибо,

как установлено экспериментально (см. п. 3.3), электрон является фундаментальной частицей и не имеет составляющих заряда.

Значения (1,00; 1,93; 2,79) магнитных моментов частиц совпадают с экспериментальными данными с точностью «вакуумных» добавок, определяющих влияние структуры пространства. Автор предполагает, что измерения магнитного момента нейтрона, равным представляемой величине 1,91, неточны. Р. Фейнман в своих работах [14] указывал практическое значение магнитного момента нейтрона, равным величине 1,93. Такое расхождение в значении магнитного момента является следствием нестабильности нейтрона, так как в свободном состоянии данная частица примерно за 15 минут превращается в протон с испусканием электрона [63].

Экспериментальная работа [15] Тейлора, Кендалла и Фридмана (нобелевские лауреаты 1990 г.) подтверждает составную модель нуклонов, хотя формы и положения этих составляющих не описаны. Эти составляющие приняты за кварки. Эта работа также указала, что структура нейтрона отличается от протона.

На основании рассмотренных магнитных моментов субатомных частиц и строения атома становится понятным приобретение телами магнитных свойств. Вещества по своей способности намагничивания подразделяются на три основные группы — диамагнетики, парамагнетики и ферромагнетики. Способность намагничивания определяется результирующим магнитным моментом атомов (молекул) вещества, что в конечном счете приводит к ослаблению внешнего магнитного поля в диа-магнетиках и к усилению его в парамагнетиках и фер-ромагнетиках, причем намагниченность ферромагнетиков сохраняется при исчезновении магнитного поля в силу упорядоченности их структуры.

Теперь вкратце еще раз рассмотрим фрактальную структуру фотона (см. п. 4.1 и рис. 4.1) и его спин. Уста-

новленная форма фотона в виде объемной восьмерки подтверждается как геометрическими представлениями, так и следующими экспериментами.

Во-первых, для сравнения со спином субатомных частиц заметим, что установленная форма фотона показывает корректное понимание целочисленной величины 1 как квантового числа спинового момента частицы света, ибо проекция фотона на плоскости есть целый круг вследствие эквивалентности восьмерки и круга. Вот почему размерность вращающейся частицы следует также представлять как масштабный коэффициент такого движения, или локальную плотность момента количества движения, что в конечном счете и определяет спин (момент количества движения) частицы (см. п. 2.8).

Во-вторых, фотоны, обладающие соответствующей энергией, взаимодействуя с атомным полемабота [15] Тейлора, Кендалла и Фридмана (нобелевские лауреаты 1990 г.) подтверждает составную модель нуклонов, хотя формы и положения этих составляющих не описаны. Эти составляющие приняты за кварки. Эта работа также указала, что структура нейтрона отличается от протона.

Теперь вкратце еще раз рассмотрим фрактальную структуру фотона (см. п. 4.1 и рис. 4.1) и его спин. Уста-

Во-вторых, фотоны, обладающие соответствующей энергией, взаимодействуя с атомным полем, превращаются в электронные и позитронные пары и следы их движения могут быть наблюдаемы. Вспомнив закон сохранения электрического заряда, приходим к выводу, что составляющие фотона противоположно заряжены, хотя сам фотон в целом электронейтрален.

Установление фрактальной структуры фотона ведет к изменению представлений об электрической природе, где носителем электромагнитного взаимодействия является электронейтральный фотон (квант), составляющие которого при этом противоположно заряжены. Это позволяет раскрыть природу электрической проводимости, что показано в п. 4.1. При этом фотоны являются как инициаторами возбуждения электронов атома, так и энергетическими носителями этого возбуждения. Электроны в проводнике не перемещаются, а остаются связанными со своими атомами. Знаем (см. ранее п. 4.2), что возникновение фотона обусловлено взаимодействием возбужденных электронов с вихревой структурой пространства атома. Фотон «набегает» на электрон, воз -никающее в результате сложное движение можно

представить как процесс образования солитонов, несущих в данном случае отрицательный (для р-полупроводников положительный) электрический заряд. Такая модель проводимости применена для описания явления сверхпроводимости (см. п. 6.1), в результате чего стало возможным синтезировать очень высокотемпературные сверхпроводящие соединения с критической температурой 373 К и выше [16].

Следовательно, такие экспериментальные результаты подтверждают правомерность фрактального, структурного представления материи, в основе которой лежит электрический заряд, но не масса. В то же время представляемые нынешней физикой законы природы оказались ошибочными. Такие неверные отражения реальной действительности мира являются общими, к примеру, не только для ядерной физики или физики космоса, но и химии, геологии, биологии, кибернетики, экономики. Поэтому нынешняя физика приказала долго работать и создать новую жизнь на этой взорванной Земле.