Приливное гравитационное взаимодействие. Природа явления выталкивания предмета из жидкости

Некорректное мировоззрение нынешней физики привело к тому, что она не могла создать теории, по­зволяющей количественно оценить величину приливов в морях и океанах. Фрактальная физика на основе про­стых соотношений объясняет как качественно, так и количественно это явление (см. Введение, п. 3 и [4]).

Рассмотрим поведение поверхности мирового океана, подобной сфере с радиусом r = 6,371 • 10⁶ м и обращен­ной в сторону Луны. Рассчитаем скорость движения v воды океана, вызываемого положительным зарядом Лу­ны Q = +6,8 • 10³ Кл (см. табл. 3.1). Исходя из движения материальной точки (см. (2.10) и (3.17)), находящейся на расстоянии R = 3,844 • 10⁸ м от заряда Q, получим:

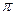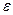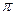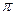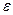v² = qQr/(m • 4 • ₀ • R²) = 6,8 • 10³ 6,371 • 10⁶/[4 • 4 • ₀^. (3,844 • 10⁸)²] = 2,1 • 10².

В данном расчете электрическая постоянная ε₀ = 1/(36 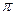• 10⁹) Ф/м, а фрактальная размерность для мате­риальной точки массой m и зарядом q принята, в соот­ветствии с (2.9), m/q = 4 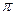(см. п. 2.5). Тогда максималь­ная высота прилива, вызываемого Луной, в соответствии

с формулой Галилея (см. п. 1.2), равна h = v²/(2g) = 2,1 • 10²/(2 • 9,8) = 10,7 м.

Из расчета можно увидеть, что максимальная высота прилива, вызываемого влиянием заряда Луны, зависит от геометрии залива (узкого места типа бухты) и струк­туры воды, а также нахождением Луны в самой близкой к Земле точке, называемой перигеем. Из действия силы можно понять, что в местах пересечения плоскости лун­ной орбиты с Землей (лунная орбита наклонена к плос­кости земной орбиты на угол в 5° [24]), Луна не оказы­вает действия на высоту прилива, однако при этом яв­ляется синхронизатором этого явления. Ее действие максимально в местах на высоких широтах, так как притяжение Луны не поднимает и не опускает уровень земных морей и океанов непосредственно, а «тянет» от­рицательно заряженную поверхность водного бассейна Земли своим положительным зарядом на освещаемой стороне и «толкает» — с противоположной стороны сво -им эффектом электростатической индукции.

Второй причиной возникновения прилива является дифференциальная гравитация Земли. Известно, что расстояние от Земли до Солнца в десять тысяч раз больше земного диаметра. Поэтому на обращенном к Солнцу участке земной поверхности сила притяжения больше, чем на противоположной стороне Земли. По­верхность водного бассейна имеет отрицательный элек­трический заряд. Выразим кинетическую энергию воды массой m и зарядом q, если в начальный момент она покоилась в точке с электрическим потенциалом φ₂ (v = 0), в форме:

(3.29)

mv₂²/2 = q( - ). (3.29)

Так как земная поверхность является сферическим конденсатором, то изменение электрического потенциала ( — ₂) равно произведению радиуса Земли (r = 6,371 • 10⁶ м) на соотношение земного диаметра 2r к расстоя-

 

 

нию R до Солнца. Поэтому выражаем скорость воды v₂ из (3.29) в виде:

(3.30)

Тогда v₂² = 2 • 6,371 • 10^б/(4 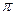• 10⁴) = 101,4, где 2r/R = 1/10⁴, m/q = 4π. Отсюда высота прилива h, вызываемого дифференциальной гравитацией Земли, равна h = v₂²/(2g) = 101,4/(2 • 9,8) = 5,2 м.

Видим, что Луна оказывает влияние на форму миро­вого океана примерно вдвое больше, чем Солнце. Здесь поясним выражение (3.30). Так как электрическое поле на обращенном к Солнцу участке земной поверхности больше, чем на противоположной стороне, то это изме­нение поля определяется знаменателем формулы Кулона (см. (2.10), (3.1) и пп. 3.3, 3.4), показатель степени рас­стояния 2 которого характеризует структуру простран­ства взаимодействия:

1/(R + г)² = 1/(R² + 2Rr + г²) « 1/(R² + 2Rr) =
= 1/(R²(1 + 2r/R)). (3.31)

Таким образом, изменение поля на противоположных участках земной поверхности, исходя из соотношения (3.31), составляет 2r/R, а изменение потенциала Земли соответственно равно 2r.r/R. Это определяет запись вы­ражения в форме (3.30). Заметим, что высота прилива, вызываемая дифферен­циальной гравитацией Земли, также зависит от геомет­рии побережья и структуры воды. Это подтверждается измерениями [58] прилива в Do Son в Тонкинском за­ливе: высокий прилив составляет лишь 3 м и повторяется только через 24 ч. Почему? Во-первых, это место лежит вблизи пересечения плоскости лунной орбиты; во-вторых, диэлектрические свойства воды таковы (здесь вода слишком отличается от свойств пресной воды), что она не успевает разрядиться, чтобы вызвать ночной прилив. При этом имеющиеся данные [58] показывают,

что высота приливов вблизи экватора составляет около 5 м, ибо Луна в этом случае является только их синхро­низатором, что подтверждает нашу теорию.

Земля вращается вокруг своей оси, положение Луны и Солнца относительно ее поверхности меняется, поэтому приливная волна перемещается за ними, и когда она приближается к берегу — начинается прилив. Макси­мальную высоту прилива h_макс, вызванного действием обоих источников, можем определить как: h_макс= 10,7 + 5,2 = 15,9 м.

Временной интервал между приливами составляет половину лунных суток, ибо ритм регулируется в данном случае в основном Луной. Самая большая высота при­лива зафиксирована [58] в бухте the Bay of Fundy (Канада), связанной с Атлантическим океаном. Высота прилива в этом месте, когда Луна находилась в перигее, составляет 15,2 м. В Пенжинской губе на Охотском море высота прилива достигает 13 м. Свойства воды здесь также близки к свойствам пресной воды. Видим, что теоретические расчеты хорошо согласуются с имеющи­мися данными.

Очевидно, что действие заряда Луны распространя­ется не только на поверхность мирового океана, но и на скрытое от нас движение плазмы. Особо следует под­черкнуть, что приливные силы, очевидно действующие на оболочку и на движение плазмы Земли, способствуют устойчивости планетной системы. Потеря спутника приведет к глобальной катастрофе (см. п. 3.9).

Рассмотренные причины возникновения приливов можно использовать для объяснения следующего явле­ния [59]: из рассказов путешественников XVII века сле­дует, что течение вод Дуная значительно медленнее ут­ром, когда лучи Солнца противодействуют его движе­нию, и ускоряется после полудня, когда лучи Солнца по­могают его течению. Нынешняя физика объясняет это изменение движения воды давлением света. С позиции фрактальной физики основной вклад в это явление

 

вносит дифференциальная гравитация — изменение электрического потенциала течения реки.

Уместно вспомнить [60], что в 20-30 годы Р. Милликен проводил исследования в области физики космических лучей. Он, в частности, предложил провести опыт, в ко -тором измерялось изменение ионизации, создаваемой космическими лучами, с глубиной в горных озерах в Калифорнии. Сравнение зависимостей, полученных для двух озер, по его мнению, подтвердили предположение, что ионизирующее излучение приходит из космоса. Те­перь мы знаем, что ионизация воды вызывается элек­тростатической индукцией Солнца. Отсюда раскрыва­ется природа явления выталкивания предмета из жид­кости (закон Архимеда), которое обусловлено влиянием электрического заряда на ее поверхности. Механику Галилея, с помощью которой мы определили высоту приливов, также следует рассматривать как предельный случай электромагнитного взаимодействия (см. п. 3.5),

Показанную природу закона Архимеда можно ис­пользовать для объяснения следующего явления: из рассказов командиров подводных лодок следует, что в погруженном походном состоянии весенней порой в каком-то месте лодка начинает мгновенно опускаться вниз. Нынешняя физика не может объяснить это явле­ние. С позиции фрактальной физики такая ситуация возникает из-за локального изменения электрического потенциала поверхности океана. Выталкивание погру­женного тела в общем зависит как от распределения электрического заряда водной поверхности, так и от временного его изменения, вызываемых как активно­стью Солнца, так и порой года. Во время половодья электрический потенциал поверхности восстанавлива­ется не мгновенно. Этот процесс характеризуется вре­менем релаксации. Такую же зависимость для ускорения свободного падения мы обнаружили в п. 3.5 по измене­нию траектории движения спутников Земли и их «забрасыванием» на орбите Луны вследствие разности

плотности зарядов ее видимого и обратного полушарий. Теперь мы можем выразить закон Архимеда в соответ­ствующих электрических величинах.

Тело массой т, погруженное в жидкость, находится в равновесии, если сила тяжести тела F_T = m • g уравно­вешивается выталкивающей силой F_A= q • Е, которая является силой, действующей на материальную точку зарядом q в электрическом поле Е (см. соотношение (3.1)):

(3.32)

 

Так как напряженность вблизи поверхности жидкости связана с поверхностной плотностью о заряда на этом участке поверхности [51], то Е = 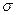/ 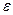₀, где ε_о элек­трическая постоянная, равная 1/(36 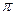• 10⁹) Ф/м. Выраже­ние для напряженности поля справедливо также для оп­ределения градиента электрического потенциала вблизи поверхности шара любого размера. Подставив в (3.32) выражение для Е, получим в системе СИ:

(3.33)

Из (3.33) значение g ускорения свободного падения равно

(3.34)

Исходя из формулы (3.34), проверим количественное значение g. Так как фрактальная размерность для мате­риальной точки массой m и зарядом q принята m/q = 4 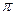(см. ранее), а поверхностная плотность а отрицательного электрического заряда Земли (в том числе и поверхности воды) по величине примерно равна 1,1 нКл/м² (см. п. 3.1), то:

Полученная величина g соответствует реальному значению ускорения свободного падения планеты.

Введем различие в определение ускорения свободного падения: g_G — глобальная и g_L — локальная размерно­сти. Ускорение g_G, входящее в силу F_T тяжести тела, оп­ределяется общим зарядом Земли и в общем не зависит от небольших локальных изменений заряда поверхности жидкости. Ускорение g_L, входящее в выталкивающую F_A силу, противоположную силе тяжести, определяется по­верхностной плотностью 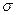заряда, которая является ло­кальной на этом участке жидкости. Поверхностная плот­ность заряда образует вертикальную компоненту элек­трического поля Земли. Глобальная и локальная размер­ности ускорения свободного падения равны по величине, если отсутствуют локальные изменения поверхностной плотности заряда. Учитывая размерности ускорения свободного падения и соотношение (3.34), закон Архи­меда выразим в системе СИ в следующей форме:

(3.35)

где ρ — плотность жидкости, V — объем вытесненной жидкости, 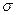— поверхностная плотность электрического заряда. Заметим при этом, величина силы F_A не зависит от того, какое вещество и в каком агрегатном состоянии заключено в вытесненном объеме. Поэтому в знамена­теле закона (3.35) вводится только электрическая по­стоянная ε₀.

Так удалось раскрыть природу явления выталкивания предмета из жидкости. Ведь толкование закона Архи­меда в течение почти 2300 лет было чисто математиче­ским. Этот закон оказался частным случаем электромаг­нитной теории тяготения. Убедиться в корректности ус­тановленного закона выталкивания можно с помощью передачи разноименных зарядов верхней, соприкасае-мой с водой крышке домашнего аквариума, что приводит к изменению глубины погружения рыбок или предметов. В реальности локальное уменьшение поверхностной плотности электрического заряда океана приводит к ос-

давлению выталкивающей силы. Этого достаточно, чтобы подводная лодка пошла ко дну.

Таким образом, фрактальная физика выявила истин­ное место закона Архимеда и механики Галилея как фрагментов механической картины мира, оказавших пагубное влияние на нынешнюю физику. Представив эти теории предельными случаями электромагнитной теории тяготения, новое учение обусловило установле­ние фундамента мироздания и продолжение разнооб­разных опытов и количественных оценок гравитацион­ного притяжения Земли, начатых древними исследова­телями.

Заметим, что мы можем объяснить теперь эффект, вызываемый кориолисовой силой [45]. Эта сила введена в 1831 г. французским ученым Г. Кориолисом для учета влияния вращения подвижной системы отсчета на от­носительное движение материальной точки. На Земле этот эффект, обусловленный ее суточным вращением применительно к водным артериям, заключается в том, что вода, движущаяся в реках вдоль земной поверхно­сти, отклоняется в Северном полушарии вправо, а в Южном — влево от направления ее движения, и про­исходит подмыв соответствующих берегов. Действитель­но, первоначально ионы воды нижних слоев начинают двигаться в направлении силы инерции, определяемой вращением. Далее их движение изменяется в сторону влияния поверхностного электрического поля реки и происходит подмыв берега в течение долгого времени. Так по-другому выглядит этот эффект с позиции новой физики.

Кстати, исследования космических лучей показали [24], что подавляющая часть первичных лучей, попадаю­щих в атмосферу Земли, имеет положительный элек­трический заряд. Это лишний раз подтверждает, что на­ша планета имеет отрицательный электрический заряд. При этом фрактальная физика, исходя из установления фундамента мироздания — электрического заряда, объ-

 

 

яснила зарядовую асимметрию Вселенной проявлением собственной природы гравитации, определяемой проти­воположными электрическими зарядами связанных тя­готением систем (см. во Введение, пп. 1, 3). Поэтому наличие таких частиц как антипротоны возможно в ок­рестностях звезд, имеющих большой положительный электрический заряд. По этой причине протонов во Вселенной неизмеримо больше, чем антипротонов. Од­нако автор теории относительности понимал мир по-другому и представил математические принципы сим­метрии глубже и фундаментальнее, чем физические за­коны [8].

Следовательно, фрактальная физика представила ко­личественную теорию приливов, подтвержденную экс­периментальными данными, раскрыла природу явления выталкивания предмета из жидкости, описала закон выталкивающей силы в электрической форме, показала электромагнитную сущность эффекта, определяемого кориолисовой силой, в подмыве берегов рек и объяснила зарядовую асимметрию Вселенной.