Фрактальная размерность субатомных частиц

Сначала применим введенное понятие фрактальной размерности для описания алгоритма постоянной тонкой

структуры α^-1 = 137,03597 [33]. Эта величина играет роль константы связи, она показывает (см. Введение, п. 5), как сильно элементарная частица взаимодействует с себе подобной, является одной из истинно фундамен­тальных постоянных природы и применима в области взаимодействий частиц, имеющих фрактальную структу­ру. Действительно, в следующем п. 2.3 показано, что константа а также описывает тонкую структуру про­странства, которая образуется в результате перехода ки-

нетической энергии фотона в потенциальную энергию, по-другому можно сказать, что структура пространства образуется комбинациями элементарных составляющих коллапсированных фотонов.

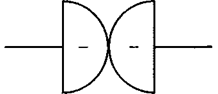
Рис. 2.2. Графическое изображение взаимодействия двух элек­тронов

На рис. 2.2 изображено взаимодействие двух электронов. Если посмотреть издалека на это взаимодействие, то увидим две маленькие пылинки, которые математики называют канторовским множеством (пылью) на прямой с глобальной размерностью D_G = ln2/ ln3 [32]. Если по­смотреть вблизи на это взаимодействие, то увидим, что соприкасаются два объемных электрических объекта, каждый из которых имеет размерность Е = 3. Вот почему в общем случае локальная размерность электриче­ской системы определяется как произведение линейных размерностей пространств с учетом протяженности прикосновения [34, 35], и в данном случае она равна D_L = 10,00049 (см. п. 4.1).

Теперь становится ясно, что определенный выше фрактал для двух взаимодействующих частиц глобально представляет собой подобие канторовскому множеству, которое получается изъятием средних третей (b = 1/3) как при формировании кривой Коха. Посмотрите на рис. 2.2: огибающая двух электронов напоминает средний сегмент кривой Коха. Поэтому глобальная размерность для двух (N = 2) взаимодействующих электронов равна D_G = ln2/ ln3 = 0,6309...

Таким образом, глобальная фрактальная размерность оценивает рост числа множеств (объектов) бесконечно малого диаметра, необходимых для того, чтобы покрыть данное множество (форму). Вообще существуют различ­ные видоизменения понятия фрактальной размерности [30], где на с. 150 представлена таблица, состоящая из 12 способов ее описания. Однако большинство авторов [27, 31] называют множество фрактальным, если его размер­ность Хаусдорфа не является целым числом и оценивает рост объектов бесконечно малого диаметра в соответ­ствии с вышеуказанным определением. В дальнейшем мы будем придерживаться единой формулировки гло­бальной фрактальной размерности в смысле Хаусдорфа.

Понятие локальной фрактальной размерности связы­вают с понятием меры множества [35, 38], в соответст­вии с известным из элементарной геометрии понятием объема. Вообще мера протяженности и искривленности множества также называется мерой Хаусдорфа. Локаль­ная фрактальная размерность характеризует объем этого множества (объекта) с учетом протяженности соприкос­новения общих элементов его форм. Понятие «объем» следует понимать как «квазиобъем», ибо отличие состоит в том, что в случае объема всякая точка, отрезок или лист имеют меру (объем) 0, а в случае квазиобъема это может быть и не так. Кроме того, схема наших построе­ний может быть распространена на некоторые квази-объемы, которые принимают и отрицательные значения. Иногда вместо понятия «квазиобъем» применяют термин «мощность», который также является аналогом понятия локальной размерности.

Во фрактальной геометрии речь идет также о новой интерпретации уже в основном известного формализма современных математических теорий, таких как теории функций и функционального анализа [36-39]. Поэтому при отображении верхнего полукруга (каким представ­ляется электрон на плоскости, что определяет спин, рав­ный 1/2; здесь для сравнения заметим, что спин фотона

равен 1, ибо восьмерка эквивалентна кругу) на область с разрезом полуоси окружности автором выявлена функ­ция конформного отображения l/Г(z), где Г(z) — гамма -функция со значением аргумента z = 1/3. Это значение аргумента определено как компонента силового поля единичного заряда на прямой взаимодействия. Область с разрезом полуоси получается за счет взаимодействия двух подобных частиц. Поэтому решение задачи о взаи­модействии двух электронов сводится к задаче кон­формного отображения. При этом впервые становится понятным физический смысл окружности отображения, как формы замкнутых силовых линий магнитного поля, возникающего вследствие изменения состояния элек­трона.

Следовательно, искомая потенциальная функция найдена как - lnГ(z). Изменение потенциала электрона за счет взаимодействия, исходя из свойств производной в ее неклассическом представлении [35, 38], можно запи­сать как - lnГ(1/3)/(2 • 10,00049), где множитель 2 найден при помощи понятия дельта - функции [34] при определении производной как предельного значения.

Исходя из установленных фрактальных размерностей взаимодействующих электронов и неклассического представления производной, константу α можем запи­сать в виде:

В данном соотношении (2.1) π - число, равное 3,14...; множитель 2 (перед ln2) определяет число взаимодейст­вующих частиц; показатель степени 2 указывает, что константа α представляет собой квадрат элементарного

заряда в естественных единицах: заряда электрона, ско­рости света, постоянной Планка (см. Введение, п. 5).

Проблема распознавания образа электрона тесно связана с отождествлением формы и поиском инвари­антных отношений. Поэтому число Зπ в данном соотно­шении представляет собой величину поверхности полу-шара единичного радиуса. Исходя из этого, форма электрона представляет собой полушар. Установленная форма электрона позволяет представить конструкции протона и нейтрона. При этом следует учитывать (см. Введение, п. 5), что субатомные частицы — не точки и не твердые полушарики, а обладают внутренней струк­турой, которую следует рассматривать как электромаг­нитные волновые сгустки, несущие электрический заряд. Так была раскрыта тайна физики, указанная Р. Фейнма-ном [14], с учетом фрактальной размерности частиц и неклассического представления производной.

В общих чертах неклассическое, или, вернее, фрак­тальное представление производной [35, 38] состоит в вычислении предела отношения:

по некоторому множеству (объекту) зарядов, «стягивающихся» к точке z, где Ф(z) — составляющая функции Ф(Е); D(z) — локальная фрактальная размер­ность объекта; z — значение заряда. Из определения производной видно, что она характеризует плотность составляющей функции Ф(Е) во всем объеме заряжен­ного объекта.

Исходя из введенного выше понятия «заряд», которое соответствует его физическому определению, установле -ны магнитные моменты протона, нейтрона и электрона [1, 5, 7]. Как известно из указанной литературы и [14], магнитный момент — это число, характеризующее от­клик частицы на внешнее магнитное поле. Здесь мы об­ратим внимание на вычисление локальных фрактальных

 

return false">ссылка скрыта

размерностей упорядоченных пар зарядов (кварков) для протона и нейтрона (см. также пп. 4.1, 4.3).

Локальная фрактальная размерность для протона со­ставляет

D_L = 10 + 2π/3 = 12,0944,

а для нейтрона — (2.3)

D_L = 10 - π/4 = 9,2146.

Эти результаты (2.3) связаны с геометрией нуклонов, показанных на рис. 4.1 и в [1, 5, 7, 33]. В отличие от нукло­нов электрон не имеет различий во внутренней структуре, его заряд отрицательный и выражается в натуральных единицах как -1.

Кварк протона зарядом (-1/3) представляет собой тончайший слой, разделяющий частицу на две равные части — кварки зарядом (+2/3). Поэтому при вычисле­нии локальной размерности (2.3) протона определено слагаемое (2π/3) с учетом особенности этого слоя, мера которого на основании формулы среднего значения [36, 37] есть произведение 2π — длины кривой (окружности), ограничивающей этот слой, на значение заряда 1/3. Два кварка нейтрона зарядом (-1/3) имеют форму сфериче­ского двуугольника со значением внутреннего угла π/4. Поэтому при определении размерности нейтрона это значение угла также учтено как отрицательное значение квазиобъема. Размерность протона и нейтрона опреде­лялась с учетом свойства аддитивности меры [40]. Зна­чение 10 соотношения (2.3) определено как произведение линейных размерностей пространств пары кварков, для каждого из которых размерность (число координат) Е = 3, а также имеющих общую прямую размерностью Е = 1.

Таким образом, благодаря введенному определению глобальной и локальной размерностей удалось ввести фрактальное (неклассическое) дифференцирование, оп-

ределить форму и структуру субатомных частиц, их ло­кальные размерности, и, в конечном счете, это привело к определению их магнитных моментов (см. п. 4.3). При этом заметим, что квантовая физика [41] не в состоянии объяснить структуры субатомных частиц и фотона и построить точную количественную теорию магнитных моментов нуклонов.