Течение жидкости в круглых трубах.

Будем рассматривать установившееся течение вязкой жидкости в трубопроводе круглого сечения. Поверхность труб полагаем гладкой, а трубу прямолинейной (рис.3.6).

Рис.3.8. К выводу баланса импульса на участке трубы

Полагаем, что выполняются так же следующие условия:

Ускорение потока равно нулю, следовательно, силы инерции отсутствуют.

Средние скорости во всех поперечных сечениях одинаковы.

Местные сопротивления отсутствуют. Существуют сопротивления по длине, вызывающие соответствующие потери напора на трение.

Давления между сечениями 1–1 и 2–2 подчиняется гидростатическому закону:

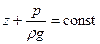На объём жидкости между сечениями 1–1 и 2–2 действуют силы внешнего давления и ( ), сила тяжести (вес жидкого цилиндра) и сила сопротивления движению . Здесь - смоченный периметр, - площадь поверхности участка трубы. Для круглой трубы .

Рис.3.9. К определению смоченного периметра.

Составим баланс импульса для участка трубы длиной между сечениями 1–1 и 2–2. Направим ось х вдоль трубы, тогда проекция силы тяжести:

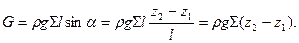Согласно (1.6.18), с учетом наших допущений:

Поделим обе части уравнения на и получим

Здесь и далее - гидравлический радиус, для круглых труб .

Запишем уравнение Бернулли:

Учитывая, что в нашем случае получим зависимость для потерь на трение в трубе:

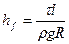. (3.5.1)

Выделим в потоке элементарный объем в виде цилиндра. С учетом формулы Ньютона 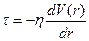будем иметь:

Разделяя переменные

После интегрирования получим

Константу С определим из условия , тогда:

. (3.5.2)

Данное выражение носит название закон распределения локальных скоростей по сечению ламинарного равномерного установившегося потока в круглой трубе.

Найдем расход жидкости с учетом этого закона

Вводя безразмерный критерий - число Рейнольдса, получим формулы для расчета потерь на трение для ламинарного потока в трубе :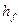

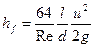. (3.5.3)

Опыты Рейнольдса. В 1883 году в Манчестерском университете Осборн Рейнольдс провел серию опытов, исследуя течение в стеклянных трубах с использованием визуализации потока краской. Через столетие Иоханнсен и Лоу повторили эксперименты на сохранившейся установке. Ниже на рис.3.8. представлены результаты данных экспериментов.

Рис.3.10. Повторение опытов О. Рейнольдса.

На входе в трубу в поток вводилась струйка подкрашенной воды. При малых скоростях движения струйка сохраняла устойчивость, но с увеличением расхода потока (скорости потока) теряла ее, при дальнейшем увеличении расхода течение становилось хаотичным – турбулентным. Значение скорости, при превышении которой нарушается устойчивость движение и в потоке возникает турбулентность, называется критической скоростью. К сожалению, критическая скорость оказалась непригодной в качестве универсального критерия для определения перехода от ламинарного типа течения к турбулентному. Для различных сред она оказалась различной. В качестве такового О. Рейнольдс предложил безразмерную величину, представляющую собой отношение потока импульса (сил инерции) к напряжению трения, впоследствии названную его именем:

. (3.5.4)

Как показали опыты для гладких труб в условиях отсутствия внешних воздействий критическое число Рейнольдса . Если в потоке жидкости или газа в круглой трубе , то поток ламинарный, если , то течение неустойчивое и в потоке возможен переход к турбулентному режиму. Следует отметить, что на практике при течение неустойчивого, то есть существует некоторый промежуток значений , в окрестности которого течение неустойчиво. Опыты также показали, что при течение полностью турбулентное (отсутствует переходной участок). Поэтому вводится еще одно критическое число Рейнольдса , а режим , носит название переходного. В последствии оказалось, что данный критерий перехода справедлив и для других течений, если в (3.5.3) вместо 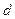использовать характерный линейный размер потока. Так если рассматривается задача об обтекании шара, и - радиус шара, тогда .

Взаимодействие жидкости с твердым телом. Данный вопрос волновал людей с очень давних пор. Первым ученым, который исследовал этот вопрос, был Аристотель. Рассматривая движение твердого тела в текущей среде, он рассуждал примерно так, тело при движении создает за собой пустоту. А так как природа не терпит пустоты, то среда заполняет пустоту и тем создает движение. Такое объяснение носило скорее философский, чем научный характер и никак не могло быть использовано на практике. Впервые научный подход к проблеме продемонстрировали Ньютон и Галилей, которые экспериментально пытались определить сопротивление при движении тел в воздухе, сбрасывая их с высоты. Ньютон на основе полученных результатов предложил вычислять силу сопротивления по формуле:

где - скорость набегающего потока, - площадь миделя (проекция контура тела на плоскость нормальную к направлению движения), - коэффициент, получивший название – коэффициент сопротивления (трения). Позднее эта формула была получена из анализа размерностей (см. параграф 1.7).

Согласно определению напряжение трения в трубе , тогда:

Тогда с учетом 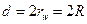, зависимость (3.5.1) можно записать в виде:

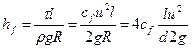Вводя обозначение , получим основную формулу которая носит название формула Дарси-Вейсбаха, и используется при расчёте как напорных трубопроводов, так и безнапорных потоков,:

, (3.5.5)

Здесь - коэффициент гидравлического трения, часто называемый коэффициентом Дарси, 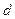- диаметр трубопровода, - скоростной напор на участке трубопровода длины . Применение этих формул связано с определением коэффициентов l. При ламинарном движении жидкости ( ) коэффициент l для труб определяется из аналитического решения (3.5.3) по формуле:

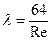. (3.5.6)

В остальных случаях приходится использовать экспериментальные данные. Впервые наиболее исчерпывающие данные о значении l были получены И. Никурадзе (рис.3.9). Как видно из графика зону I – ламинарного течения отделяет от зоны III – турбулентного потока ( ), зона переходного режима течения. Течение потока в этой зоне неустойчивое и поэтому на практике стараются такие режимы течения не использовать. В этой зоне может быть вычислено по формуле И.П. Гинзбурга:

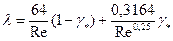Здесь - коэффициент перемежаемости.

Зона турбулентных режимов течения может быть разбита на три подобласти, отмеченные на рис.3.9. цифрами в кружочках.

Область (1) – область «гидравлически гладких» труб, в которой коэффициент трения не зависит от шероховатости. Согласно А.Д. Альтщулю ей соответствует диапазон изменения числа Рейнольдса:

. (3.5.7)

А сама зона на графике отделена наклонной прямой. В этом случае используется формула Блазиуса:

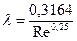. (3.5.8)

Рис.3.11. Результаты Никурадзе.

I – область ламинарного течения, II – переходная область, III – область турбулентного течения. 1 - ; 2 - ; 3 - ; 4 - ; 5 - ; 6 - .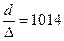

В области (3) коэффициент сопротивления зависит только от относительной шероховатости труб и не зависит от числа Рейнольдса. Данную область называется «область квадратичного сопротивления», потому что потери напора в этом случае пропорциональны квадрату скорости . Такой тип течения возникает при и в ней используется формула Б. Н. Шифринсона:

. (3.5.9)

В «переходной» области (2) при , когда шероховатость труб оказывает существенное влияние, удобно использовать формулу А.Д. Альтшуля:

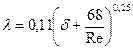. (3.5.8)

Таблица для определения коэффициента гидравлического трения

Режим течения	Критерий	Зависимость для
ламинарный
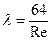
переходный		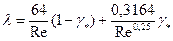, Не рекомендуется для проектирования
турбулентный	«гидравлически гладких» труб
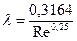
«переходный»
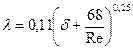
«квадратичного сопротивления»

Приведенными зависимостями не исчерпываются все эмпирические зависимости для , существуют также формулы Ф. А. Шевелёва, Н. З. Френкеля, Л. А. Тепакса, Н. Ф. Фёдорова и других. Так для режима «квадратичного сопротивления» используют формулу Никурадзе , для режима «гидравлически гладких» труб формулу Конакова 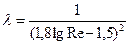, несколько более сложные для расчета.

Кроме потерь на трение в трубопроводных системах имеют место потери на местных сопротивлениях. В этом случае уравнение Бернулли имеет вид:

(3.5.9)

Здесь 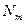- число местных сопротивлений на участке, - коэффициент i-го местного сопротивления, который может быть определен и таблицы.

Вход в трубу из резервуара
Выход из трубы в резервуар
Колено с закруглением
Колено без закругления
Сетка на входе в трубу
Открытая задвижка
Кран пробковый открытый
Вентиль нормальный открытый
Обратный клапан на входе в трубу
Обратный клапан в трубе
Внезапное расширение
Внезапное сужение
Диафрагма
Линейное Расширение		4 8 15 30 60 90 0,08 0,16 0,35 0,80 0,95 1,07