Потенциальный и полный гидродинамические напоры. Пьезометрическая линия.

Удельные потоки энергии, т.е. обусловленные движением жидкости потоки энергии через живое сечение, отнесенные к весовому расходу жид­кости, называют напорами.

Введем понятия:

потенциальный напор ; (3.4.1)

скоростной напор ; (3.4.2)

полный, или гидродинамический напор ; (3.4.3)

потеря напора между сечениями 1 - 1 и 2 - 2 . (3.4.4)

Принимая такие обозначения, запишем уравнение Бернулли в виде

. (3.4.5)

При решении задач о движении в трубах и каналах часто, задав плоскость сравнения в каждом живом сечении потока, определяют потенциальный и полный напоры и указывают геометрическое место точек, отвечающих этим напорам, в соответствии с их геометрической интерпретацией (рис. 3.4).

Если в каждом живом сечении отложить от плоскости сравнения по вертикали величину потенциального напора , то совокупность точек образует пьезометрическую линию , которую будем показывать пунктиром. Аналогично, если в каждом сечении отложить по вертикали от плоскости сравнения величину полного напора

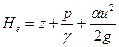, то со­вокупность точек образует напорную линию , показываемую сплош­ной линией, данную линию также называют линией гидравлического уклона.

Рис. 3.4. Пьезометрическая Р - Р и напорная Е - Е линии.

Отметим, что понятие напора было введено для тех сечений потока, где движение равномерное или плавноизменяющееся. На участке, где движение резкоизменяющееся (например, между сечениями а - а и b - b на рис. 3.4), напорная и пьезометрическая линии строятся условно путем их экстраполяции из областей, где движение плавноизменяющееся.

На участке с равномерным движением (например, между сечениями 1 -1 и а - а) потери напора потока на каждую единицу длины будут одина­ковы (структура потока во всех сечениях одинакова, следовательно, и ра­бота всех внутренних сил, определяющих потерю напора, в одинаковых объемах будет одинакова), поэтому напорная линия Е - Е на таких участ­ках будет прямой. Пьезометрическая линия, которая располагается всегда ниже напорной на величину , будет прямой, параллельной на­порной линии. Важными характеристиками этих линий являются их продольные уклоны, т.е. отношение разности напоров на участке равно­мерного движения к расстоянию между сечениями, в которых эти напо­ры вычислены.

Уклон напорной линии называется гидравлическим и обозначается Je, а уклон пьезометрической линии называется пьезометрическим и обо­значается Jp. Например, для участка потока между сечениями 1 - 1 и а - а

. (3.4.5)

 

Рис.3.5. Пьезометрическая Р - Р и напорная Е - Е линии при плавноизменяющемся движении.

Если движение плавноизменяющееся, то и потери напора на каждой единице длины вдоль потока будут переменны, и скоростной напор будет меняться вдоль оси потока. При этом линии Е-Е и Р-Р будут кривыми (рис.3.5). В этом случае гидравлический и пьезо­метрический уклоны определяются для каждого сечения как уклоны на элементарном участке длиной , прилегающем к сечению, т.е. как ук­лоны касательной к соответствующим линиям:

; (3.4.6)

(3.4.7)

Здесь знак минус показывает, что положительным считается уклон, при котором геодезические отметки линий Е - Е и Р - Р уменьшаются вдоль потока. При равномерном движении (рис. 3.4)

. (3.4.8)

Следовательно, гидравлический уклон численно равен удельной (на единицу весового расхода) диссипированной мощности в объеме потока, приходящейся на единицу длины. В заключение отметим два важных положения.

1. Потери напора - величина положительная (механическая энер­гия жидкости при движении мо­жет лишь уменьшаться, переходя в тепло), поэтому полный напор в сечениях, расположенных ниже по течению, всегда меньше напора в сечениях, расположенных выше по течению. Отметки напорной линии вдоль потока все­гда уменьшаются, и гидравлический уклон всегда положителен (Je > 0).

2. Если часть кинетической энергии жидкости при её движении переходит в потенциальную, то потенциальный напор может возрастать, при этом отметки пьезометрической линии возрастают.

Рис.3.6. Расходомер Вентури.

Рассмотрим еще один случай использования уравнения Бернулли - расходомер Вентури (рис.3.6). Этот прибор представляет собой трубу с сужением, для измерения давления в которой вставлены два пьезометра, в узкой и широкой части. Поместим плоскость отсчета на ось трубы и рассмотри сечения, в которых установлены пьезометры. Запишем уравнение Бернулли для этих сечений, полагая жидкость идеальной ( ):

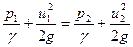
Из условия постоянства расхода имеем . Введем обозначение и после несложных преобразований получим соотношение для скорости потока в трубе и объемного расхода жидкости в трубе:

.

Здесь - постоянная расходомера.

Для вязкой жидкости:

,

где - коэффициент расхода расходомера. Из изложенного видно, что для измерения расхода можно использовать и другие устройства, если известны зависимости гидравлических потерь на них от параметров потока. Достаточно поставить датчики давления до и после такого устройства. Более подробно этот вопрос будет рассмотрен ниже.

Рис.3.7. Трубка Пито.

Еще одним прибором для измерения скорости (расхода) является гидродинамическая трубка Пито (рис.3.7). Полагая жидкость идеальной, получим следующую запись уравнения Бернулли:

Учитывая 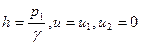. Получаем зависимость для скорости потока в виде:

.

Существует так же класс тахометрических приборов для измерения расхода потока. Они могут быть турбинными, шариковыми и камерными. В таких приборах измеряют частоту вращения или акустических колебаний потока. В последние годы получили распространение так же электромагнитные расходомеры, в которых измеряется изменение емкостных или электропроводых свойств.