Сила давления жидкости на плоскую поверхность. Центр давления. Гидростатический парадокс. Давление жидкости на криволинейные поверхности.

На практике часто требуется знать силы, действующие на те или иные гидротехнические конструкции и сооружения. Для наглядности такие нагрузки принято изображать в виде эпюр гидростатического давления – графического распределения давления вдоль поверхности (рис.2.6).

Рис.2.6. Пример построения эпюр давления.

Сила давления на плоскую поверхность. Рассмотрим произвольную площадку , расположенную на плоскости , имеющую наклон градусов к плоскости свободной поверхности (рис.2.7). Над поверхностью находится жидкость с плотностью .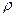

Рис.2.7. К определению силы давления на плоскую поверхность.

Для удобства изложения развернем плоскость вокруг оси и совместим ее с плоскостью рисунка. Рассмотрим элементарную площадку на плоскости и принадлежащую поверхности , в окрестности точки , находящейся на глубине . Сила избыточного давления на будет равна . Здесь - среднее значение давления на . Так как, - мало, то можно принять . Следовательно , а суммарное давление на площадку равное искомой силе :

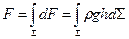Учтем, что 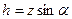, тогда:

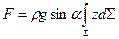Из теоретической механики известно, что 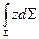- статический момент площади , относительно оси 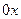, который равен произведению площади на плечо, равное расстоянию от оси 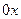до центра тяжести 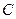площади :

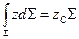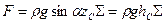. (2.3.1)

Таким образом, сила избыточного давления на любую площадку равна произведению гидростатического давления в центре тяжести площадки на ее площадь.

Соответственно сила абсолютного давления на площадку:

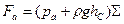Центр давления – точка приложения результирующей силы давления жидкости. Обозначим эту точку буквой 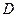. Согласно теоретической механике момент равнодействующей силы относительно оси равен сумме моментов сил ее составляющих. Выберем за таковую ось 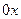. В нашем случае:

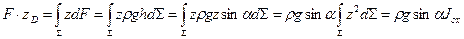Здесь 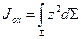- момент инерции площади относительно оси 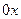. Следовательно:

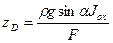С учетом (2.3.1) имеем:

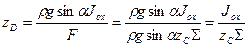. (2.3.2)

Из теоретической механики известно:

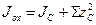Здесь 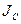- момент инерции относительно оси, проходящий через центр масс и параллельной оси 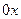. Окончательно получим:

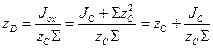. (2.3.3)

Следовательно, центр давления всегда расположен ниже центра масс, или совпадает с ним если площадка горизонтальная.

Для простых геометрических фигур 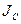могут быть вычислены по формулам.

Для прямоугольника, сторона основания которого параллельна оси 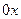и равна 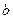, а высота :

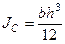Для равнобедренного треугольника:

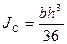Для круга диаметром :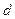

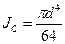
Координата 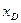для симметричных фигур совпадает с координатой центра масс 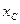, которая принадлежит оси симметрии. В случае отсутствия симметрии координата, определяется аналогично координате 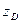, но в этом случае рассматриваются моменты относительно оси .

Гидростатический парадокс. Рассмотрим сосуды различной формы, но имеющими одинаковую площадь основания (рис.2.8). Несмотря различный вес жидкости в сосудах, сила действующая на их дно будет одинаковая.

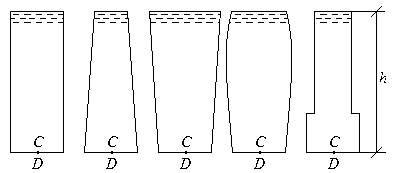
Рис.2.8. Гидростатический парадокс.

Сила давления жидкости на криволинейные поверхности. Рассмотрим криволинейную поверхность , находящуюся на некоторой глубине. Поместим систему координат на свободной поверхности, направив ось вниз перпендикулярно поверхности. Выделим в жидкости цилиндр, так чтобы его боковая поверхность была параллельна оси , и проходила по границе поверхности на дне, до пересечения со свободной поверхностью, такой выделенный объем называют телом давления. Пусть - внешняя нормаль к поверхности , тогда на элемент поверхности будет действовать сила, имеющая проекции 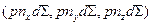. Интегрируя по поверхности, и учитывая зависимость избыточного давления от глубины 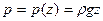, получим:

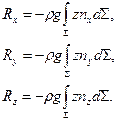
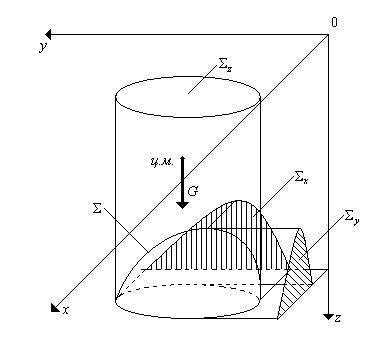
Рис.2.9. К определению силы действующей на криволинейную поверхность.

Для вертикальной составляющей можно использовать и более простой способ вычисления. Условия равновесия жидкого цилиндра можно записать в виде:

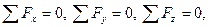
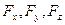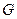Здесь - проекции сил действующих на жидкий цилиндр. Рассмотрим проекцию на ось . Сила веса жидкости в теле давления - цилиндре, нижняя поверхность которого совпадает с поверхностью , а боковая поверхность достроена вертикально до пересечения со свободной поверхностью, приложенная к его центру масс должна уравновешиваться проекцией на 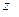реакции поверхности на цилиндр. Следовательно:

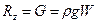. (2.2.4)

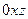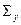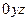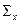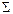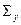Спроектируем поверхность на плоскость - и плоскость - , при этом необходимо учитывать знак проекции. Условимся считать проекцию положительной, если - внешняя нормаль к поверхности направлена на соответствующую плоскость, и отрицательной если направлена от плоскости. Так, например, для поверхностей вращения вокруг оси параллельной , проекции и 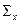равны 0, так как равны сумме положительной и отрицательной площадей, равных по модулю. Таким образом, проекции силы действующей на криволинейную поверхность на оси :

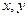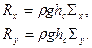(2.2.5)

Здесь 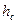- глубина на которой находится центр масс соответствующей проекции поверхности .

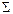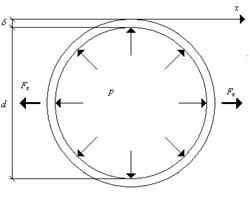Рис.2.10. Сечение трубы

Определение толщины стенок цилиндрических резервуаров и труб. Рассмотрим действие избыточного давления жидкости на трубу круглого поперечного сечения длиной (рис.2.10). Проекция силы 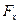согласно (2.2.5) есть:

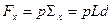Данная сила уравновешивается упругими силами растяжения. Растягивающее напряжение можно определить разделив данную силу на площадь стенки трубы:

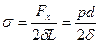Зная - допустимое напряжение материала трубы, можно вычислить толщину стенок трубы 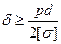.