Комплексная форма интеграла Фурье.

Пусть функция может быть представлена интегралом Фурье (функция отвечает условиям Дирихле и абсолютно интегрируема, то есть - сходится). Запишем для этой функции в действительной форме интеграл Фурье:
, где

;

Используя формулы Эйлера (4.14) и (4.15), преобразуем подынтегральное выражение (5.5):

 

Домножим числитель и знаменатель второй дроби на мнимую единицу i:

Обозначим:

 

при . Тогда подынтегральная функция в выражении (5.5) запишется в виде:

 

и

При этом

 

 

Т.е. (5.9)

 

Равенство (5.9) получено при условии, что , но можно показать, что формула (5.9) справедлива и при .

То есть равенство (5.9) справедливо при всех действительных значениях u. Окончательно можно записать комплексную форму интеграла Фурье:

при

(5.10)

 

Пример: записать интеграл Фурье в комплексной форме для функции

( )

 

, где

Вычислим для заданного примера коэффициент c(u):

 

c(u) - спектральная характеристика функции называется спектром функции

Итак, интеграл Фурье в комплексной форме для заданной функции имеет следующий вид:

Перейдем от комплексной формы интеграла Фурье к действительной форме интеграла Фурье для этой же функции.

Сложим первое и второе равенства, тогда

 

То есть:

Вычтем из первого равенства второе, тогда:

 

 

Тогда коэффициент b(u) соответственно равен:

 

Интеграл Фурье для данной функции в обычной, действительной форме примет вид:

 

Пример: представить интегралом Фурье в комплексной форме функцию

 

 

- кусочно-гладкая и кусочно-монотонная, абсолютно интегрируемая функция, так как

 

 

то есть данную функцию можно представить с помощью интеграла Фурье:

, где

 

 

По формуле Эйлера , в нашем случае меняем на .

 

Тогда:

При вычислениях учитывали, что

Тогда комплексная форма интеграла Фурье для данной функции примет вид:

Перейдем к действительной форме интеграла Фурье для той же функции:

Действительная форма интеграла Фурье для данной функции примет вид:

Приложение.

Варианты индивидуальных домашних заданий.

Вариант № 1

1. Исследовать ряд на сходимость.

 

2. Найти область сходимости степенного ряда.

 

3. Разложить в ряд Тейлора по степеням “ x “ функцию

 

, найти интервал сходимости ряда к .

4. Разложить в ряд Фурье на интервале (0 ; π) по косинусам функцию:

 

Вариант № 2

1. Исследовать ряд на сходимость.

2. Найти область сходимости степенного ряда.

 

3. Вычислить приближенно

учитывая 2 члена разложения подынтегральной функции. Оценить погрешность приближения.

4. Разложить в ряд Фурье функцию по синусам:

0 < x < π

Вариант № 3

1. Исследовать ряд на сходимость.

 

 

2. Найти область сходимости степенного ряда.

 

 

3. Вычислить с точностью до 0.001

 

 

4. Разложить в ряд Фурье функцию по синусам.

 

T = 2π

 

Вариант № 4

1. Исследовать ряд на сходимость.

 

 

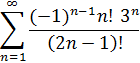
2. Найти область сходимости степенного ряда.

 

 

3. Разложить в ряд Маклорена функцию

, найти интервал сходимости ряда к .

 

4. Разложить в ряд Фурье функцию:

по синусам.

Вариант № 5

1. Исследовать ряд на сходимость.

 

2. Найти область сходимости степенного ряда.

 

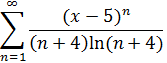
3. Вычислить с точностью до 0,001

 

4. Разложить в ряд Фурье функцию:

 

по синусам.

 

Вариант № 6

1. Исследовать ряд на сходимость.

 

2. Найти область сходимости степенного ряда.

 

3. Разложить в ряд Маклорена функцию

 

, найти интервал сходимости ряда к .

 

4. Разложить в ряд Фурье

 

на отрезке 0 < x < π по косинусам.

 

Вариант № 7

1. Исследовать ряд на сходимость.

 

 

2. Найти область сходимости степенного ряда.

 

3. Разложить в ряд Тейлора по степеням (x +3) функцию

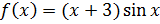, найти интервал сходимости ряда к .

 

4. Представить интегралом Фурье функцию:

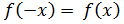
Вариант № 8

1. Исследовать ряд на сходимость.

 

 

2. Найти область сходимости степенного ряда.

 

 

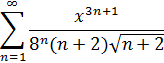
3.Разложить в ряд Тейлора по степеням “ x “ функцию

 

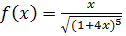, найти интервал сходимости ряда к .

 

4.Представить интегралом Фурье функцию:

 

Вариант № 9

1. Исследовать ряд на сходимость

 

2. Найти область сходимости степенного ряда

 

3. Разложить в ряд Тейлора по степени Х функцию

 

найти интервал сходимость к f(x)

 

4. Разложить функцию в ряд Фурье по косинусам

Вариант №10

1. Исследовать ряд на сходимость

 

2. Найти область сходимости степенного ряда

 

3. Вычислить с точностью до 0.001

 

 

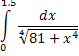
4. Разложить в ряд Фурье функцию на отрезке (0; 1) по косинусам

 

Вариант № 11

1. Исследовать ряд на сходимость

 

2. Найти область сходимости степенного ряда

 

3. Разложить в ряд Тейлора по степеням (х-2) функцию

 

найти интервал сходимость к f(x)

 

4. Разложить в ряд Фурье функцию на интервале (0;2π)

 

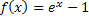
Вариант № 12

1. Исследовать ряд на сходимость

 

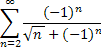
2. Найти область сходимости степенного ряда

 

3. Разложить функцию в ряд Тейлора по степеням X, определить интервал сходимости

4. Разложить в ряд Фурье периодическую функцию с , если:

 

Вариант №13

1. Исследовать ряд на сходимость

 

2. Найти область сходимости степенного ряда

 

3. Разложить в ряд Тейлора по степеням (х+1) функцию

 

найти интервал сходимость к f(x)

 

4. Представить функцию рядом Фурье на интервале (-π, π)

 

 

Вариант №14

1. Исследовать ряд на сходимость

 

2. Найти область сходимости степенного ряда

 

3. Вычислить с точностью до 0.001

 

4. Разложить функцию в ряд Фурье на интервале (0, π) по синусам

 

Вариант №15

1. Исследовать ряд на сходимость числовой ряд

 

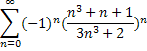
2. Найти область сходимости степенного ряда

 

3. Разложить в ряд Тейлора по степеням X функцию

 

найти интервал сходимости ряда к f(x).

 

4. Представить рядом Фурье периодическую функцию с Т=π

Вариант №16

1. Исследовать числовой ряд на сходимость

 

2. Найти область сходимости степенного ряда

 

3. Разложить в ряд Тейлора по степеням X функцию

найти интервал сходимость к f(x).

 

4. Представить рядом Фурье функцию на интервале (-3, 3).

Вариант № 17

1. Исследовать числовой ряд на сходимость:

 

 

2. Найти область сходимости степенного ряда:

 

 

3. Вычислить с точностью до 0,001:

 

4. Представить рядом Фурье функцию: на интервале (-1<x< 1)

 

Вариант № 18

1. Исследовать числовой ряд на сходимость:

 

 

2. Найти область сходимости степенного ряда:

 

 

3. Разложить в ряд Тейлора по степеням x функцию:

 

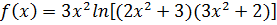, найти интервал сходимости ряда к

 

4. Разложить по косинусам на интервале функцию:

Вариант №19

1. Исследовать числовой ряд на сходимость:

 

 

2. Найти область сходимости степенного ряда:

 

 

3. Вычислить с точностью до 0,001:

 

 

4. Разложить в ряд Фурье функцию , 0<x<2 с периодом T=2

 

Вариант №20

1. Исследовать числовой ряд на сходимость:

 

 

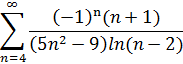
2. Найти область сходимости степенного ряда:

 

 

3. Разложить в ряд Тейлора по степеням (x+1) функцию: 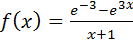, найти интервал сходимости ряда к .

 

4. Разложить в ряд Фурье на интервале 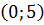функцию f(x) по синусам:

 

Вариант №21

1. Исследовать числовой ряд на сходимость:

 

 

2. Найти область сходимости функционального ряда:

 

 

3. Вычислить определенный интеграл с точностью до 0,001:

 

 

4. Разложить в ряд Фурье на интервале 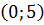функцию:

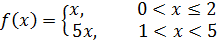по косинусам.

 

Вариант №22

1. Исследовать числовой ряд на сходимость:

 

2. Найти область сходимости функционального ряда:

3. Вычислить с точностью до 0,001:

4. Представить функцию интегралом Фурье:

 

Вариант №23

1. Исследовать числовой ряд на сходимость:

 

2. Найти область сходимости функционального ряда:

 

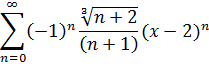
3. Разложить в ряд Тейлора по степеням x функцию:

, найти интервал сходимости ряда к .

 

4. Представить функцию интегралом Фурье:

 

 

Вариант №24

1. Исследовать числовой ряд на сходимость:

 

 

2. Найти область сходимости функционального ряда:

 

 

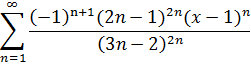
3. Вычислить определенный интеграл с точностью до 0,001:

 

4. Представить функцию интегралом Фурье: