Задачи выпуклого программирования
Рассмотрим задачу нелинейного программирования:
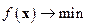 , (7.27)
, (7.27)
 , (7.28)
, (7.28)
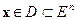 ,
, 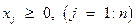 , (7.29)
, (7.29)
где f и  – некоторые функции n переменных
– некоторые функции n переменных  . Эта задача от рассмотренных ранее задач условием,
. Эта задача от рассмотренных ранее задач условием,  , которое добавлено из соображений удобства. В практических задачах, как правило,
, которое добавлено из соображений удобства. В практических задачах, как правило,  или
или  .
.
Для решения сформулированной задачи в такой общей постановке не существует универсальных методов. Однако для отдельных классов задач, в которых сделаны дополнительные ограничения относительно свойств функций  и
и  , разработаны эффективные методы их решения. В частности, ряд таких методов имеется для решения задач нелинейного программирования (7.27)…(7.29) при условии, что f – вогнутая (выпуклая) функция и область допустимых решений, определяемая ограничениями (7.28)…(7.29), – выпуклая.
, разработаны эффективные методы их решения. В частности, ряд таких методов имеется для решения задач нелинейного программирования (7.27)…(7.29) при условии, что f – вогнутая (выпуклая) функция и область допустимых решений, определяемая ограничениями (7.28)…(7.29), – выпуклая.
Введем нормальную функцию Лагранжа вида:
 , (7.30)
, (7.30)

Нормальная функция Лагранжа проще функции Лагранжа, удобнее для вычислений. Однако правило для нее не всегда верно. Путь функции f(x), g(x) определены, непрерывны и дифференцируемы на  . Если х* – точка условного относительного минимума, то найдется нулевой вектор
. Если х* – точка условного относительного минимума, то найдется нулевой вектор  такой, что
такой, что
 .
.
Решения задачи (7.27)…(7.29) тесно связаны с седловыми точками функции Лагранжа.
Определение 1. Точка  , где
, где  называется седловой точкой функции Лагранжа (7.21), если при всех x
называется седловой точкой функции Лагранжа (7.21), если при всех x  выполняется неравенства:
выполняется неравенства:

График некоторой функции, имеющей седловую точку, где x и λ – скаляры, изображены на рис. 7.7. Седловая точка функции является результатом ее минимизации по x и максимизации по  .
.
Таким образом, если  зафиксировать равным λ* и рассматривать
зафиксировать равным λ* и рассматривать  как функцию только x, то х* будет точкой глобального минимума. Аналогично, если рассматривать эту функцию как функцию от
как функцию только x, то х* будет точкой глобального минимума. Аналогично, если рассматривать эту функцию как функцию от  при фиксированном x, равном х*, то λ* будет точкой глобального максимума.
при фиксированном x, равном х*, то λ* будет точкой глобального максимума.

Рис. 7.7. График функции, имеющей седловую точку
Лемма. Пара векторов  при
при  является седловой точкой функции Лагранжа тогда и только тогда, когда выполнены следующие условия:
является седловой точкой функции Лагранжа тогда и только тогда, когда выполнены следующие условия:

 или
или 

 .
.
Теорема 7.3. (достаточное условие оптимальности). Если пара векторов  , где
, где  , является седловой точкой функции Лагранжа, то х*– точка глобального минимума в задаче (7.27)…(7.29) и выполнены условия дополняющей нежесткости
, является седловой точкой функции Лагранжа, то х*– точка глобального минимума в задаче (7.27)…(7.29) и выполнены условия дополняющей нежесткости  .
.
В соответствии с теоремой 7.3, если удается найти седловую точку  функции Лагранжа (7.30), тем самым будет решена задача (7.27)…(7.29). Теоретически такой подход безупречен. Однако его практическая реализация возможна не всегда. Дело в том, что если функция f, g не выпуклы, то функция Лагранжа часто не имеет ни одной седловой точки. Более того, даже если указанные функции и множество выпуклы и оптимальное решение задачи (7.27)…(7.29) существует, то в некоторых «вырожденных» случаях функция Лагранжа также может не обладать ни одной седловой точкой.
функции Лагранжа (7.30), тем самым будет решена задача (7.27)…(7.29). Теоретически такой подход безупречен. Однако его практическая реализация возможна не всегда. Дело в том, что если функция f, g не выпуклы, то функция Лагранжа часто не имеет ни одной седловой точки. Более того, даже если указанные функции и множество выпуклы и оптимальное решение задачи (7.27)…(7.29) существует, то в некоторых «вырожденных» случаях функция Лагранжа также может не обладать ни одной седловой точкой.
Условия, при выполнении которых хотя бы одна седловая точка функции Лагранжа всегда существует, сформулированы в следующем утверждении.
Теорема 7.4. (существования седловой точки) (Куна-Таккера). Предположим, что множество  выпукло, функции
выпукло, функции  выпуклы на нем и имеют условие Слейтера: найдется такая точка
выпуклы на нем и имеют условие Слейтера: найдется такая точка 
 , что
, что  < 0, i = 1: m. Пусть
< 0, i = 1: m. Пусть 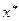 – точка глобального минимума в задаче (7.27)…(7.29). Тогда найдется такой вектор
– точка глобального минимума в задаче (7.27)…(7.29). Тогда найдется такой вектор  , что пара
, что пара  образует седловую точку функции Лагранжа, т.е. для всех
образует седловую точку функции Лагранжа, т.е. для всех  и x
и x  выполняются неравенства:
выполняются неравенства:
 .
.
Условие Слейтера исключает присутствие в задаче ограничений типа равенств. Это условие означает, что среди точек множества D найдется хотя бы одна, в которой все ограничения являются неактивными.
Если предположить, что целевая функция f и функция  непрерывно дифференцируемы, то теорема Куна-Таккера может быть дополнена аналитическими выражениями, определяющими необходимые и достаточные условия того, чтобы точка
непрерывно дифференцируемы, то теорема Куна-Таккера может быть дополнена аналитическими выражениями, определяющими необходимые и достаточные условия того, чтобы точка  была седловой точкой функции Лагранжа, т.е. являлась решением задачи выпуклого программирования. Эти выражения имеют вид:
была седловой точкой функции Лагранжа, т.е. являлась решением задачи выпуклого программирования. Эти выражения имеют вид:
 (7.31)
(7.31)
 (7.32)
(7.32)
 (7.33)
(7.33)
 (7.34)
(7.34)
 (7.35)
(7.35)
 (7.36)
(7.36)
где  и
и  – значения соответствующих частных производных функции Лагранжа, вычисленных в седловой точке.
– значения соответствующих частных производных функции Лагранжа, вычисленных в седловой точке.
Всем отмеченным выше требованиям, позволяющим записать необходимые и достаточные условия для седловой точки  функции Лагранжа в виде указанных выражений, удовлетворяет сформулированная ниже задача квадратичного программирования.
функции Лагранжа в виде указанных выражений, удовлетворяет сформулированная ниже задача квадратичного программирования.