Дополнение множества
Дополнением множества Х называется разность I и Х.

Свойства дополнения:
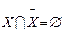 |
1. Множество Х и его дополнение не имеют общих элементов
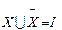 |
2.Любой элемент I принадлежит или множеству Х или его дополнению.
1. Из формулы 2 вытекает еще одно важное свойство
Тема 2.4
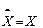
Законы и тождества алгебры множеств
X ∩ Y = Y ∩ X - коммутативности пересечения
(X∩ Y) ∩Z =X∩ (Y∩ Z)=X∩ Y∩Z– ассоциативности пересечения
X U Y= Y U Y- коммутативности объединения
(X U Y) U Z =X U (Y U Z)=X U Y U Z – ассоциативности объединения
XU Æ = X
X∩ Æ = Æ
X∩ I = Х
XUI = I
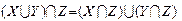 |
Транзитивности
 |
Если вы внимательно присмотритесь, то заметите аналогии между законами логики высказываний и алгебры множеств. Это не случайно. Эти два раздела математики тесно связаны и на уровне понимания природы объектов, и на уровне формализации.
Дело в том, что термин алгебра в своем роде имя нарицательное. Под ним понимается раздел математики, изучающий алгебраические операции, а природа объектов, к которым применяются эти операции, не важна. Говоря об алгебре логики или об алгебре множеств, мы более всего уделяли внимание операциям, определенным над допустимыми в данной теории объектами, свойствам этих операций. Еще одним хорошо известным вам примером алгебры, является алгебра чисел, к которой все выписанные законы также применимы. Проводя аналогии между этими алгебрами, мы можем сказать
| Алгебра чисел | Алгебра логики | Алгебра множеств | |
| Объекты | Числа | Высказывания | Множества |
| Операция + | Сложение | Дизъюнкция | Объединения |
| Операция * | Умножение | Конъюнкция | Пересечение |
| Нулевой элемент | Ложь | Пустое множество | |
| Единичный элемент | Истина | Универсальное множество |
И хотя каждая из рассматриваемых нами теорий имеет свои специфические законы, не освещенные или просто неинтересные в рамках другой теории, можно говорить, что утверждения алгебры множеств можно рассматривать с точки зрения алгебры логики и наоборот.
Тема 2.5. Понятие кортежа. Декартово произведение множеств
Определение: упорядоченный набор, конечная последовательность каких-либо объектов, внешне связанных определенным положением, которое они занимают в данной совокупности объектов, называется упорядоченным множеством или кортежем.
Объекты, входящие в кортеж называются компонентами.
Число компонент кортежа называется его длиной. В отличие от множества в кортеже могут быть и одинаковые компоненты, и порядок расположения элементов важен.
Например: можно как кортеж рассматривать буквы в слове, слова в фразе, абзацы в тексте.
Определение: Декартовым произведением двух не пустых множеств Х и У называется множество ХхУ, состоящее из всех упорядоченных пар,
ХхУ = {(x,y) / x Î X; y Î Y)
Если одно из множеств пустое, то и ХхУ пустое.
Например:X = {1, 2}
Y = {1, 2, 4}
XxY = {(1,1); (1,2);(1,4);(2,1);(2,2);(2,4)}
YxX = {(1,1);(1,2);(2,1);(2,2);(4,1);(4,2)}
Обратим внимание, что речь идет об упорядоченных парах, т.е. в отличии от множеств (1,2)¹(2,1)
Примером декартова произведения является система координат : пара чисел, обозначающие широту и долготу. Частный случай декартова произведения множества самого на себя называется степенью множества. Так, привычная вам система координат на плоскости есть не что иное, как декартово произведение множества вещественных чисел само на себя, или квадрат множества вещественных чисел.
RxR=R
и любая точка на плоскости задается (х, у) .
Из приведенного примера видно, что
ХхУ¹УхХ
Тема 2.6 Понятия соответствия, отображения, отношения, функции.
Рассмотрим два множества А и В. Элементы этих множеств могут каким-либо образом сопоставляться друг другу, образуя пары (а, b). Если задан способ такого сопоставления, то говорят что между множествами установлено соответствие. При этом совершенно необязательно, чтобы в сопоставлении участвовали все элементы множеств А и В.
Определение: Соответствием между множествами А и В называется любое подмножество R= АхВ - декартова произведения множеств.
Например: Рассмотрим два множества:
А={Гагарин, Дунаевский, Носов, Рахманинов}
В={1900,1901,….2000} - годы 20 века.
Установим соответствие между этими двумя множествами, например, человек – год рождения.
Г = {(Гагарин, 1934);(Дунаевский, 1900);(Носов,1908)}
(Рахманинов, 1973) – естественно не вошел в множество
Другим примером соответствия, установленного между этими множествами, может быть такое: человек – год смерти.
Г’ = {(Гагарин, 1968);(Дунаевский,1955);(Носов,1986),(Рахманинов,1943)}
Определение: Множество DR, такое что,
DR, = {a Î A : $ b ÎB (a,b) Î R}
называется областью определения соответствия R.
Определение: Множество DR, такое что,
BR, = { b ÎB: (a,b) Î R}
называется областью значений соответствия R, или образом.
Таким образом, соответствие можно задать ООС, ОЗС и законом, определяющим соответствие.
Определение: Если каждому элементу множества Х ставится в соответствие один или более элемент множества У, то говорят что задано отображение Х на У.
В ранее приведенном примере соответствие человек - год рождения – не является отображением (т.к. не каждому элементу множества Х ставится в соответствие элемент из множества У) , а соответствие (человек, год смерти) – является отображением.
Определение: Функцией называется однозначное отображение Х на У. Т.е. такое отображение f, что если
(х1,y1) Î f и (х2,y2) Î f из х1 = х2 следует y1 = y2
При этом множества Х и У могут совпадать.
Определение: Если область определения отображения и область значения отображения совпадают, то отображение называется отношением.
Отметим некоторые возможные свойства отношений:
1. Рефлексивность. хГх – истинно
2. Антирефлексивность. хГх – ложно
3. Симметричность. хГу Þ уГх
4. Антисимметричность. хГу и уГх Þ у=х
5. Несимметричность. хГу истинно, то уГх - ложно
6. Транзитивность. хГу и уГz Þ хГz
Пример: Алфавит русского языка, как и любого другого языка – это упорядоченное множество букв. Назовем отношение между элементами этого множества отношением предшествования и обозначим его значком <.
Мы знаем, что а<б, б<в. И т.д.
Укажем свойства этого отношения:
1. f<f – ложно, т.к. ни одна из букв не предшествует сама себе. Т.е. отношение предшествования антирефлексивно.
2. Если f<s – истинно, то s<f – ложно. Т.е. отношение предшествования несимметрично.
3. Если f<s и s<t, то f<t Отношение транзитивно
Т.о. отношение предшествования, которое мы ввели на множестве букв русского языка антирефлексивно, несимметрично и транзитивно.
Пример: Можно ввести на множестве из предыдущего примера отношение "непосредственно предшествует", основываясь на уже существующем и исследованном нами отношении "предшествует".
Будем говорить, что х непосредственно предшествует у, если x<y и Ø$ z: x<z и z<y.
Упражнение: Определите свойства этого отношения самостоятельно.
Тема 2.7 Типы отношений.
Теперь опишем несколько часто употребляемых типов отношений.
Отношение эквивалентности:
Некоторые элементы множества можно рассматривать как эквивалентные , если любой из этих элементов при некотором рассмотрении можно заменить другим.
Примером отношения эквивалентности могут быть:
Отношение "быть синонимом" на множестве слов русского языка;
Отношение "иметь одинаковый остаток при делении на 3" на множестве целых чисел;
Отношение "быть параллельной" на множестве прямых одной плоскости.
Отношение "быть братом" на множестве людей.
Определение: Отношение эквивалентности – это бинарное отношение на множестве Х, удовлетворяющее следующим условиям:
1. ХºХ – рефлексивность
2. ХºУ ® УºХ – симметричность
3. ХºУ и УºZ ® ХºZ транзитивность
Т.е. отношение эквивалентности удовлетворяет следующим условиям: каждый элемент эквивалентен сам себе, не важен порядок, в котором рассматриваются эквивалентные элементы, и если два элементы эквивалентны третьему, то они эквивалентны между собой.
Упражнение: Покажите, что все примеры отношения эквивалентности обладают перечисленными свойствами.
Отношение строгого порядка:
Часто приходится сталкиваться с отношениями, определяющими некоторый порядок расположения элементов множества.
Примеры отношения строгого порядка:
отношения "быть больше", "быть меньше" на множестве действительных чисел;
отношение строгого включения на множестве подмножеств данного множества.
Отношение "быть предком" на множестве людей.
Определение: Отношение строгого порядка – это бинарное отношение на множестве Х, удовлетворяющее следующим условиям:
1. Х<Х – антирефлексивность
2. Х<У и У<Х – несимметричность
3. Х<У и У<Z ® Х<Z - транзитивность
Отношение нестрогого порядка:
Примеры отношения строгого порядка:
отношение £ на множестве действительных чисел;
отношение Í на множестве подмножеств данного множества.
Определение: Отношение нестрогого порядка – это бинарное отношение на множестве Х, удовлетворяющее следующим условиям:
1. Х£Х – рефлексивность
2. Х£У и У£Х®Х=У – антисимметричность
3. Х£У и У£Z ® Х£Z – транзитивность
4.
Тема 2.8 Верхняя и нижняя границы множества. Разбиение множества на классы эквивалентности
Эти понятия введены на любом подмножестве действительных чисел.
Определение: Верхней гранью некоторого множества действительных чисел, называется любое число, ограничивающее это множество сверху, т.е. удовлетворяющее условию:
"хÎC х£x , x - называется верхней границей множества Х
Определение: Точной верхней гранью множества называется наименьшая из верхних граней множества и обозначается sup(X).
Определение: Нижней гранью некоторого множества действительных чисел, называется число, ограничивающее это множество снизу, т.е. удовлетворяющее условию:
"хÎC х³x , x - называется верхней границей множества Х.
Определение: Точной нижней гранью, называется наибольшая из нижних граней множества и обозначается inf(X).
Одной из наиболее часто встречающихся операций над множествами является операция разбиения множества на систему подмножеств.
Пример: Система курсов данного факультета, система групп данного курса.
Пример: Если N – множество натуральных чисел, А – множество четных чисел, В – множество нечетных чисел, то {А,В} – будет разбиением множества N. Это же множество может быть разбито по остатку от деления на 3.
Чтобы дать формальное определение разбиения множества рассмотрим некоторое множества М и систему множеств ММ = {1…n}
Определение: Система ММ называется разбиением множества М, если она удовлетворяет следующим условиям:
1. любое множество из ММ является подмножеством М
2. Любые два множества из ММ являются непересекающимися
3. Объединение всех множеств из ММ дает М.
Это понятие тесно связанно с отношением эквивалентности. Если рассматривать М как множество, на котором введено отношение эквивалентности, то подмножество элементов, эквивалентных некоторому элементу из М называется классом эквивалентности. Если рассматривать на множестве студентов отношение «быть в одной группе», то группа, в которой учится студент Иванов, будет классом эквивалентности, эквивалентным студенту Иванову.
Из свойства транзитивности отношения эквивалентности следует, что все студенты, принадлежащие одному классу эквивалентности, эквивалентны между собой и всякий элемент из М может находиться только в одном классе. Но в таком случае полная система классов эквивалентности является разбиением множества. Т.о. каждому отношения эквивалентности на множестве М соответствует некоторое разбиение множества М на классы. Эти понятия называют сопряженными.