Решето Сундарама

Решето Сундарама – алгоритм поиска всех простых чисел в некотором заданном диапазоне. Он был разработан в 1934 году ныне безызвестным студентом из Индии С. П. Сундарамом.

Принцип работы алгоритма Сундарама сводится, как и в его знаменитом предшественнике, к последовательному отсеиванию всех ненужных чисел. Но у него есть одна небольшая особенность: результатом работы алгоритма будет последовательность простых чисел из диапазона от 2 до удвоенного значения граничного числа. Допустим необходимо получить все простые числа до некоторого n, тогда выходными данными будут все простые числа от 2 до 2n+1.

Решето Сундарама из ряда натуральных чисел, не превышающих n, исключает числа вида 2ij+i+j. Результат данного выражения, ни при каких значениях входящих в него переменных, не превышает n (2ij+i+j≤n). Соблюдая это условие, а также то, что i всегда меньше или равно j, переменные i и j пробегают все натуральные значения из множеств:

i = 1, 2, 3, …,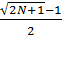

j = i, i+1, i+2, …,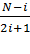

После исключения всех ненужных чисел необходимо увеличить каждое оставшиеся число в два раза и прибавить единицу (2i+1). Итоговое множество будет содержать числа: 2, 3, …, 2n+1.

Код программы на C++:

 

void Sundaram(bool A[], int n) //Решето Сундарама

{

int i, j;

for (i=1; i<=n; i++) A[i]=true;

i=1;

j=1;

while ((2*i*j+i+j)<=n)

{

while (j<=(n-i)/(2*i+1))

{

A[2*i*j+i+j]=false;

j++;

}

i++;

j=i;

}

for (i=1; i<=n; i++)

if (A[i]) cout<<2*i+1<<" ";

}

 

void main() //главная функция

{

int n, i, j;

bool A[1000];

cout<<"n > "; cin>>n;

cout<<"Простые числа: 2 ";

Sundaram(A, n);

}

 

Код программы на Pascal:

 

type arr=array [1..1000] of boolean;

var

n: integer;

A: arr;

procedure Sundaram(A: arr; n: integer); {Решето Сундарама}

var i, j: integer;

begin

for i:=1 to n do A[i]:=true;

i:=1;

j:=1;

while (2*i*j+i+j)<=n do

begin

while j<=(n-i)/(2*i+1) do

begin

A[2*i*j+i+j]:=false;

j:=j+1;

end;

i:=i+1;

j:=i;

end;

write(2, ' ');

for i:=1 to n do

if A[i] then write(2*i+1, ' ');

end;

 

begin {основной блок программы}

write('n > ');

read(n);

writeln('Простые числа:');

Sundaram(A, n);

end.