АВЛ-дерево

АВЛ-дерево – структура данных, изобретенная в 1968 году двумя советскими математиками: Евгением Михайловичем Ландисом и Георгием Максимовичем Адельсон-Вельским. Прежде чем дать конструктивное определение АВЛ-дереву, сделаем это для сбалансированного двоичного дерева поиска. Сбалансированным называется такое двоичное дерево поиска, в котором высота каждого из поддеревьев, имеющих общий корень, отличается не более чем на некоторую константу k, и при этом выполняются условия характерные для двоичного дерева поиска. АВЛ-дерево – сбалансированное двоичное дерево поиска с k=1. Для его узлов определен коэффициент сбалансированности (balance factor). Balance factor – это разность высот правого и левого поддеревьев, принимающая одно значение из множества {-1, 0, 1}. Ниже изображен пример АВЛ-дерева, каждому узлу которого поставлен в соответствие его реальный коэффициент сбалансированности.

 

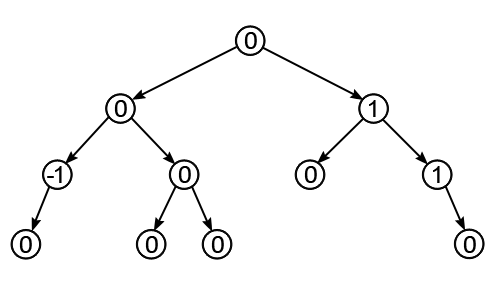
Рисунок 4.6 – АВЛ-дерево

 

Положим B_i – коэффициент сбалансированности узла T_i (i – номер узла, отсчитываемый сверху вниз от корневого узла по уровням слева направо). Balance factor узла T_i рассчитывается следующим образом. Пусть функция h() с параметрами T_i и L возвращает высоту левого поддерева L узла T_i, а с T_i и R – правого. Тогда B_i=h(T_i, R)-h(T_i, L). Например, B₄=-1, так как h(T₄, R)-h(T₄, L)=0-1=-1.

Сбалансированное дерево эффективно в обработке, что следует из следующих рассуждений. Максимальное количество шагов, которое может потребоваться для обнаружения нужного узла, равно количеству уровней самого бинарного дерева поиска. А так как поддеревья сбалансированного дерева, «растущие» из произвольного корня, практически симметричны, то и его листья расположены на сравнительно невысоком уровне, т. е. высота дерева сводиться к оптимальному минимуму. Поэтому критерий баланса положительно сказывается на общей производительности. Но в процессе обработки АВЛ-дерева, балансировка может нарушиться, тогда потребуется осуществить операцию балансировки. Помимо нее, над АВЛ-деревом определены операции вставки и удаления элемента, выполнение которых может привести к дисбалансу дерева.

Доказано, что высота АВЛ-дерева, имеющего n узлов, примерно равна log₂ n. Беря в виду это, а также то, то, что время выполнения операций добавления и удаления напрямую зависит от операции поиска, получим временную сложность трех операций для худшего и среднего случая – O(log n).

Прежде чем рассматривать основные операции над АВЛ-деревом, определим структуру для представления его узлов, а также три специальные функции:

 

struct Node

{

int key;

char height;

Node *right;

Node *left;

Node(int k) { key=k; height=1; left=right=0; }

};

 

char height(Node *p)

{

if (p) return p->height;

else return 0;

}

 

int BF(Node *p)

{ return height(p->right)-height(p->left); }

 

void OverHeight(Node *p)

{

char hleft=height(p->left);

char hright=height(p->right);

p->height=(hleft>hright ? hleft : hright)+1;

}

 

Структура Node описывает узлы АВЛ-дерева. Ее поля right и left являются указателями на правое и левое поддеревья. Поле key хранит ключ узла, height – высоту поддерева. Функция-конструктор создает новый узел. Функции height и BF вычисляют коэффициент сбалансированности узла, а OverHeight – корректирует значение поля height, затронутое в процессе балансировки.