Введение
Список – абстрактный тип данных, реализующий упорядоченный набор значений. Списки отличаются от массивов тем, что доступ к их элементам осуществляется последовательно, в то время как массивы – структура данных произвольного доступа. Список имеет несколько реализаций в виде структур данных, например, таких как: связный список, стек, очередь и дек.
Связный список – это структура данных, представляющая собой конечное множество упорядоченных элементов, связанных друг с другом посредствам указателей. Каждый элемент структуры содержит поле с какой-либо информацией, а также указатель на следующий элемент. В отличие от массива, к элементам списка нет произвольного доступа.
По типу связности выделяют односвязные, двусвязные, XOR-связные, кольцевые и некоторые другие виды списков.
В односвязном списке (рис. 2.1) начальным элементом является Head list (голова списка [произвольное наименование]), а все остальное называется хвостом. Хвост списка составляют элементы, разделенные на две части: информационную (поле info) и указательную (поле next). В последнем элементе вместо указателя, содержится признак конца списка – nil.

Рисунок 2.1 – Односвязный список
Односвязный список не слишком удобен, т. к. из одной точки есть возможность попасть лишь в следующую точку, двигаясь тем самым в конец списка. Когда кроме указателя на следующий элемент есть указатель и на предыдущий, то такой список называется двусвязным (рис. 2.2).
Возможность двигаться как вперед, так и назад полезна для выполнения некоторых операций, но дополнительные указатели требуют задействования большего количества памяти, чем таковой необходимо в эквивалентном односвязном списке.

Рисунок 2.2 – Двусвязный список
Для двух видов списков описанных выше существует подвид, называемый кольцевым (циклическим) списком (рис. 2.3). Сделать из односвязного списка кольцевой можно добавив всего лишь один указатель в последний элемент, так чтобы он ссылался на первый. А для двусвязного потребуется два указателя: на первый и последний элементы.

Рисунок 2.3 – Кольцевой связный список
В каждом элементе XOR-связного списка хранится только один адрес. Он определяется выполнением над адресами логической операции XOR (исключающее «ИЛИ», строгая дизъюнкция). Например, имеем список элементов: A, B, C, D, E. Чтобы узнать куда двигаться из элемента C, необходимо выполнить над адресами элементов B и D операцию XOR.
Помимо рассмотренных видов списочных структур есть и другие способы организации данных по типу «список», но они, как правило, во многом схожи с разобранными, поэтому здесь они будут опущены.
Кроме различия по связям, списки делятся по методам работы с данными. О некоторых таких методах сказано далее.
Стек характерен тем, что получить доступ к его элементом можно лишь с одного конца, называемого вершиной стека, иначе говоря: стек – структура данных, функционирующая по принципу LIFO (last in — first out, «последним пришёл — первым вышел»). Изобразить эту структуру данных лучше в виде вертикального списка (рис. 2.4), например, стопки каких-либо вещей, где чтобы воспользоваться одной из них нужно поднять все те вещи, что лежат выше нее, а положить предмет можно лишь на вверх стопки.
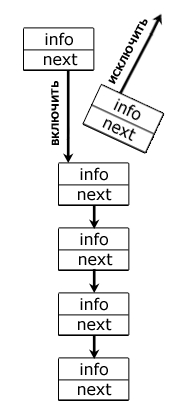
Рисунок 2.4 – Стек
В показанном на рисунке односвязном списке операции над элементами происходят строго с одного конца: для включения нужного элемента в пятую по счету ячейку необходимо исключить тот элемент, который занимает эту позицию. Если бы было, например 6 элементов, а вставить конкретный элемент требовалось также в пятую ячейку, то исключить бы пришлось уже два элемента.
Структура данных Очередь (рис. 2.5) использует принцип организации FIFO (First In, First Out — «первым пришёл — первым вышел»). В некотором смысле такой метод более справедлив, чем тот, по которому функционирует стек, ведь простое правило, лежащее в основе привычных очередей в различные магазины, больницы считается вполне справедливым, а именно оно является базисом этой структуры. Пусть данное наблюдение будет примером. Строго говоря, очередь – это список, добавление элементов в который допустимо, лишь в его конец, а их извлечение производиться с другой стороны, называемой началом списка.

Рисунок 2.5 – Очередь
Элементу необходимо пройти весь список, прежде чем он станет доступным. В этом отношении работа со следующей структурой покажется несколько более удобной.
Дек (deque — double ended queue, «двухсторонняя очередь») – стек с двумя концами (рис. 2.6). Действительно, несмотря конкретный перевод, дек можно определять не только как двухстороннюю очередь, но и как стек, имеющий два конца. Это означает, что данный вид списка позволяет добавлять элементы в начало и в конец, и то же самое справедливо для операции извлечения.
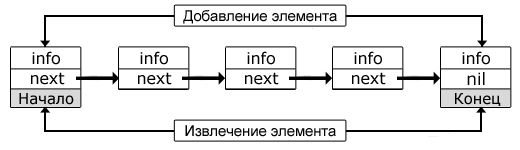
Рисунок 2.6 – Дек
Эта структура одновременно функционирует по двум способам организации данных: FIFO и LIFO. Поэтому ее допустимо отнести к отдельной программной единице, полученной в результате суммирования двух предыдущих видов списка.