Закрытое хеширование

Первый метод назывался открытым, потому что он позволял хранить сколь угодно много элементов, а при закрытом хешировании их количество ограниченно размером хеш-таблицы. В отличие от открытого хеширования закрытое не требует каких-либо дополнительных структур данных. В ячейках таблицы хранятся не указатели, а элементы исходного массива, доступ к каждому из которых осуществляется по хеш-значению ключа, при этом одна ячейка может содержать только один элемент.

Сам процесс заполнения хеш-таблицы с использованием алгоритма закрытого хеширования осуществляется следующим образом:

1. имеется изначально пустая хеш-таблица T размера m, массив A размера n (m≥n) и хеш-функция h(), пригодная для обработки ключей массива A;

2. элемент x_i, ключ которого key_i, помещается в одну из ячеек хеш-таблицы, руководствуясь следующим правилом:

· если h(key_i) – номер свободной ячейки таблицы T, то в последнюю записывается x_i;

· если h(key_i) – номер уже занятой ячейки таблицы T, то на занятость проверяется другая ячейка, если она свободна, то x_i заноситься в нее, иначе вновь проверяется другая ячейка, и так до тех пор, пока не найдется свободная или окажется, что все m ячеек таблицы заполнены.

Последовательность, в которой просматриваются ячейки хеш-таблицы, называется последовательностью проб. Последовательность проб задается специальной функцией, например интервал между просматриваемыми ячейками может вычисляться линейно, или увеличиваться на некоторое изменяющееся значение.

Рассмотрим метод закрытого хеширования на примере построения хеш-таблицы. Положим, имеется целочисленный массив A, состоящий из 9 элементов:

{A[key]=data, здесь key – ключ, data – некоторые данные}

A[13]=8, A[56]=4, A[79]=1, A[37]=5, A[41]=2, A[76]=9, A[51]=3, A[93]=9, A[30]=1

Также есть хеш-таблица размера m=10, и хеш-функция h(key)=key % m (% – операция «остаток от деления»). Заполним хеш-таблицу элементами массив A:

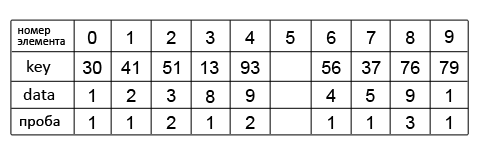
Для расстановки элементов использовалась выбранная формула. Подставив ключ, например первого элемента в нее получим: h(13) = 13 % 10 = 3, поэтому его номер в хеш-таблице 3. Последовательное добавление элементов приведет к возникновению коллизии при обработке элемента A[76]. Хеш-значение его ключа 6, но в хеш-таблице ячейка с таким номером уже занята. Используя формулу линейного пробирования (один из типов последовательности проб) h_i(key)=(h(key) + i) % m (i – число проверок, после первой проверки i=0), продолжим поиск свободной ячейки. Применим функцию при i=1: h₁(76)=7; убедившись, что ячейка 7 занята, продолжаем поиск, увеличив i на 1: h₂(76)=8. Ячейка 8 свободна, помещаем в нее элемент. Этот же метод используем и для всех остальных элементов.