Двумерные дискретные случайные величины.

Пусть на вероятностном пространстве (Ω,S,P) заданы дискретные случайные величины , тогда двумерную случайную величину будем называть дискретной.

Пусть - все возможные значения , - все возможные значения . Как мы уже знаем, с помощью вероятностей и определяются законы распределения случайных величин ξ и η. Ясно, что возможные значения двумерной случайной величины содержатся среди пар точек на плоскости. Рассмотрим вероятности

 

Тогда с помощью этих вероятностей можно найти вероятность 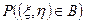, где В - произвольное множество точек плоскости, а именно:

. (3)

Отсюда вытекает, что исчерпывающей характеристикой (законом распределения) двумерной дискретной системы может служить таблица

 

			…		…
			…		…
			…		…
…	…	…	…	…	…
			…		…
…	…	…	…	…	…

 

Эта таблица называется совместным законом распределения случайных величин ξ и η.

Из определения следует, что

и . (4)

Любая таблица такого вида задает некоторый закон совместного распределения пары случайных величин, который и называется двумерным законом распределения.

Из двумерного закона распределения можно получить одномерные законы распределения для ξ и для η:

, (5)

поскольку событие 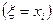является суммой несовместных событий , а событие суммой несовместных событий .

Законы распределения (5) иногда называются маргинальными законами первоначального двумерного распределения.

Пример. В урне лежат четыре шара , 2 белых, 1 чёрный и 1 синий. Из урны наугад извлекают два шара (без возвращения) Пусть ξ - число чёрных, а η - число синих шаров в выборке. Составить для системы закон распределения.

Решение. В данном случае возможные значения для и η есть 0 и 1 . Имеем:

(событие ( ) наступает только при одном из исходов опыта), (событие ( ) наступает только при двух исходах),

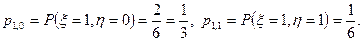
Искомый закон распределения задаётся следующей таблицей: