Аксиоматический подход к теории вероятностей

 

Из определения вероятности (см §2) ясно видно, что вероятность описывает некоторую реальную закономерность, проявляющуюся при массовом повторении случайного испытания. Однако для построения математической теории важно не только установить естественно-научное значение основных понятий, но и формально перечислить их основные свойства. Так, в геометрии простейшие, лежащие в основе построения теории свойства точек и прямых, перечисляются в аксиомах, например: через две различные точки проходит одна и только одна прямая. Точно так же, логическое построение теории вероятностей основано на фиксации первичных, не подлежащих определению понятий данной теории. Их основные свойства формулируются в виде ряда аксиом. После этого все предложения теории (иначе говоря, все теоремы) выводятся из аксиом строго логическим путем, без обращения к посторонним понятиям опыта, наглядности, устойчивости частот и т.д.

Современная аксиоматика теории вероятностей принадлежит советскому математику А.Н. Колмогорову.

Приведём сначала некоторые предварительные соображения.

Заметим, что среди событий по отношению к данному опыту можно выделить такие, которые являются простейшими, элементарными.

Элементарные события характеризуются тем, что при каждом осуществлении опыта наступает одно и только одно из них и, что любое событие А, связанное с данным опытом, должно распадаться на элементарные, т.е. представляться в виде суммы некоторого множества элементарных событий.

Пример1. В опыте с бросанием игральной кости события 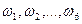, где означает выпадение i очков, являются элементарными. Действительно, любое событие, представляющее интерес в связи с бросанием игральной кости, формулируется как некоторое условие на число очков (например: число очков чётное, число очков превосходит 3 и т.д.). Отсюда ясно, что каждое событие, связанное с данным опытом, распадается на элементарные события .

Пример2. Пусть опыт заключается в «бросании» точки в области Ω на плоскости. Элементарное событие – это попадание точки в определенную точку области Ω. Ясно, что суммами таких событий исчерпываются все мыслимые исходы опыта. В данном примере, в отличие от предыдущего, множество элементарных событий бесконечно. Можно считать его совпадающим с множеством всех точек области Ω.

Возвращаясь к общей ситуации, обозначим через Ω множество всех элементарных событий для данного опыта. Каждому событию А, связанному с данным опытом, можно сопоставить подмножество множества Ω; это подмножество состоит из тех элементарных событий, на которые распадается А. В аксиоматике Колмогорова событие А отождествляется с соответствующим подмножеством в Ω. В такой интерпретации, например: событие « на игральной кости выпало нечётное число очков» есть подмножество в множестве , а событие «точка попала в подобласть Д области Ω на Рис.1.» есть подмножество множества Ω, состоящее из всех точек Д указанной подобласти.

 

 

 

Рис.1

 

Такой подход к понятию события удобен тем, что благодаря ему, понятия суммы cобытий, произведения cобытий и противоположного события приобретают естественно теоретико-множественный смысл, а именно: сумма событий А и В превращается в объединение соответствующих подмножеств, произведение событий А и В – в пересечение этих подмножеств, а противоположное событие - в дополнению к подмножеству А в Ω.

Таким образом, математическая формализация модели случайного опыта разбивается на две группы аксиом.