Основные справочные формулы

· Закон Ома в дифференциальной форме имеет вид:

j=σE, (3.29)

где j –плотность тока;

Е – напряженность электрического поля;

σ – удельная электропроводность материала.

В свою очередь можно записать:

, (3.30)

где ρ – удельное сопротивление материала;

n – концентрация носителей заряда;

μ– подвижность носителей заряда.

· Вероятность состояния электронов подчиняется функции Ферми-Дирака:

(3.31)

· Распределение Ферми по энергиям для свободных электронов в металле:

при Т > 0

; (3.32)

при Т = 0

, (3.33)

где – концентрация электронов, энергия которых заключена в интервале

;

E_F – уровень Ферми.

· Для концентрации электронов в зоне проводимости можно получить выражение:

(3.34)

где E_F(0)– уровень Ферми при Т = 0.

Из последнего выражения можно получить:

, (3.35)

где (3.36) – максимальный заполненный энергетический уровень в металле при Т = 0.

Средняя тепловая энергия электронов в металле:

. (3.37)

Температура вырождения имеет вид:

. (3.38)

В собственном полупроводнике концентрации электронов в зоне проводимости и дырок в валентной зоне равны:

(3.39)

где – эффективная плотность состояний в зоне проводимости;

Е_с – дно зоны проводимости;

 

(3.40)

где – эффективная плотность состояний в валентной зоне;

Е_ν – потолок валентной зоны.

 

С учетом электронейтральности для концентрации носителей в собственном полупроводнике можно получить следующее выражение:

, (3.41)

где – ширина запрещенной зоны.

 

· Уровень Ферми в собственном полупроводнике имеет следующее значение:

. (3.42)

В примесных полупроводниках концентрация носителей заряда в разных температурных диапазонах описывается различными формулами. Для рабочего температурного диапазона они имеют вид:

, (3.43)

,

где N_д, N_a – концентрации донорной и акцепторной примеси;

– энергия ионизации донорной или акцепторной примеси.

(3.44)

 

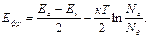(3.45)

Существует связь между концентрацией основных и неосновных носителей:

(3.46)

 

Постоянная Холла R_н в некторых случаях может быть найдена по формуле:

, (3.46)

где I – ток через образец;

d – толщина образца;

п – концентрация носителей заряда;

В – индукция магнитного поля.

· Уравнение непрерывности описывает скорость изменения концентрации носителей в полупроводнике. Для одномерного случая можно записать:

(3.48)

где D_n – коэффициент диффузии;

g – скорость генерации;

Dn – избыточная концентрация электронов;

τ_n – время жизни электронов.

 

Аналогичное выражение можно записать для дырок. Выражение (3.48) описывает общий случай, когда действует диффузионный и дрейфовый токи, процессы генерации и рекомбинации. При уменьшении числа факторов уравнение упрощается.

 

· Прохождение тока через тонкие пленки основано на различных механизмах. Токи надбарьерной инжекции

j=AT² exp(-φ₀/kT)· , (3.49)

где φ₀ – высота потенциального барьера.

Если токи, ограничены пространственным зарядом, то

I≈9/8 εε₀μ_nSU²/d³ (3.50)

где S – площадь контакта;

d – толщина контакта.

U – разность потенциалов.