Задачи для самостоятельного решения
1. Ток I течет по тонкому проводнику, который имеет вид правильного n-уголь-ника, вписанного в окружность радиусом R. Найти выражение для магнитной индукции в центре данного контура и исследовать его при n®¥ . Вычислить величину индукции при I=2 А, R=5 см и n=6.
2. Найти магнитную индукцию в центре контура, имеющего вид прямоугольника, если его диагональ d=16 см, угол между диагоналями j=30о и ток в контуре I=5,0 А.
3. По тонкому проволочному кольцу течет ток. Не изменяя силы тока в контуре, ему придали форму квадрата. Во сколько раз изменилась магнитная индукция в центре квадрата.
 4. Найти магнитную индукцию в т.О контура с током
4. Найти магнитную индукцию в т.О контура с током
I=5.0 А (рис. 1.12, а-в):
а) -a=20 см, b=40 см, j=90о ,
б) -a=20 см, b=40 см ,
в) -a=60 см (равносторонний треугольник, О - точка пересечения высот).
 5. Определить магнитную индукцию в т.О, если радиус изогнутой части проводника с током I=0,8 А равен R=5 см; прямолинейные участки проводника предполагаются очень длинными (рис. 1.13, а-в).
5. Определить магнитную индукцию в т.О, если радиус изогнутой части проводника с током I=0,8 А равен R=5 см; прямолинейные участки проводника предполагаются очень длинными (рис. 1.13, а-в).
6. На тороид малого поперечного сечения намотано равномерно N=2,5×103 витков провода, по которому течет ток. Найти отношение h магнитной индукции внутри тороида к магнитной индукции в центре тороида.
7. Два круговых витка расположены в двух взаимно перпендикулярных плоскостях так, что центры этих витков совпадают. Радиус каждого витка R=2 см, токи в витках I1=5 А и I2=10 А. Найти магнитную индукцию в центре витков.

8. Найти магнитную индукцию в т.О, если проводник с током I=8 А имеет вид, показанный на рис. 1.14, а-в. Радиус изогнутой части проводника R=100 мм.

9. Найти магнитную индукцию в т. О, если проводник с током I=10 А имеет вид, показанный на рис. 1.15, а-в. Радиус изогнутой части проводника R=0,2 м, прямолинейные участки проводника очень длинные.
10. Две плоские катушки R=5 см каждая расположены в параллельных плоскостях на расстоянии d=10 см друг от друга. Число витков каждой катушки N=20, по ним протекают токи I1=I2=2 А. Найти:
а) распределение магнитной индукции вдоль оси системы (между катушками) и построить график В(х), х меняется от 0 до 10 см с шагом 2 см;
б) значение силы тока в катушках, при котором в центре системы будет скомпенсирована горизонтальная составляющая магнитного поля Земли, равная 2×10-5Тл.
11. Два бесконечно длинных прямых проводника скрещены под прямым углом. По проводникам текут токи I1=80 А и I2=60 А. Расстояние между проводниками d=20 см. Чему равна магнитная индукция (рис. 1.16):
а) в точке А;
б) в точке B;
с) в точке C.
 12. По двум бесконечно длинным прямым параллельным проводникам текут токи I1=100 А и I2=50 А в противоположных направлениях. Расстояние между проводниками d=20 см. Определить магнитную индукцию (рис. 1.17):
12. По двум бесконечно длинным прямым параллельным проводникам текут токи I1=100 А и I2=50 А в противоположных направлениях. Расстояние между проводниками d=20 см. Определить магнитную индукцию (рис. 1.17):
а) в точке А; б) в точке В; с) в точке С.
13. Длинный проводник с током I=5,0 А изогнут под прямым углом. Найти:
а) магнитную индукцию в точке, которая отстоит от плоскости проводника на h=35 см и находится на перпендикуляре к проводникам, проходящем через точку изгиба;
б) магнитную индукцию в точке, лежащей на биссектрисе угла и отстоящей от вершины на l=14 см (внутри угла);
в) магнитную индукцию в точке, лежащей на биссектрисе угла и отстоящей от вершины на l=14 см (вне угла).
14. На рис. 1.18 изображены сечения трех прямолинейных бесконечно длинных проводников с токами. Расстояния АВ=ВС=5 см, токи I1=I2=10 А и I3=20 А. Найти:
 а) точку на прямой АС, в которой магнитная индукция поля, созданного токами I1, I2, I3, равна нулю;
а) точку на прямой АС, в которой магнитная индукция поля, созданного токами I1, I2, I3, равна нулю;
б) точку на прямой АС, в которой магнитная индукция поля, созданного токами, равна нулю, если токи текут в одном направлении.
 15. Ток I=6,28 А течет по длинному проводнику, сечение которого имеет форму тонкого полукольца радиусом R=20 см (рис. 1.19). Найти величину и направление магнитной индукции в точке О.
15. Ток I=6,28 А течет по длинному проводнику, сечение которого имеет форму тонкого полукольца радиусом R=20 см (рис. 1.19). Найти величину и направление магнитной индукции в точке О.
16. Тонкий провод (с изоляцией) образует плоскую спираль из N=100 плотно расположенных витков, по которым течет ток
I=8 мА. Радиусы внутреннего и внешнего витков равны a=50 мм b=100 мм. Найти:
а) магнитную индукцию в центре спирали; б) магнитный момент спирали.
17. Тонкая лента шириной l=40 см свернута в трубку радиусом R=30 см. По ленте течет равномерно распределенный по ширине ленты ток I=200 А. Определить магнитную индукцию поля на оси трубки:
а) в средней точке; б) на расстоянии 10 см от средней точки; в) на расстоянии
20 см от средней точки.
18. Постоянный ток протекает по длинному прямому проводнику круглого сечения. Радиус провода R=5 мм. Плотность тока в проводе изменяется по закону j=jo×(r/R), jo=1×106A/м2. Найти индукцию магнитного поля этого тока как функцию расстояния от оси провода, построить график В(r). Вычислить магнитную индукцию:
а) на расстоянии r=R/2;
б) на расстоянии r=2R.
19. По тонкому стержню длиной l=20 см равномерно распределен заряд
q=2,4×10-7 Кл. Стержень приведен во вращение с постоянной угловой скоростью w=10 с-1 относительно оси, перпендикулярной стержню и проходящей на расстоянии 10 см от его ближайшего конца (вне стержня). Определить:
а) магнитную индукцию на оси в плоскости вращения;
б) магнитный момент, обусловленный вращением стержня.
20. Однородный ток плотности j течет внутри неограниченной пластины толщиной 2d параллельно ее поверхности. Найти магнитную индукцию как функцию расстояния x от средней плоскости пластины. Магнитная проницаемость всюду равна единице. Построить график В=f(x).
21. Постоянный ток течет по длинному прямому проводнику круглого сечения. Радиус провода R=5 мм. Плотность тока изменяется по сечению проводника по закону j=jo(1-r/R), jo=2×106А/м2. Найти поток вектора магнитной индукции через одну из половин осевого сечения в расчете на один метр его длины.
22. По проводнику в виде тонкостенной трубы радиусом R течет параллельно оси трубы ток силой I. Найти магнитную индукцию как функцию расстояния r от оси трубы (внутри трубы и вне нее). Магнитная проницаемость всюду равна единице. Построить график B=f(r).
23. В одной плоскости с длинным прямым проводом, по которому течет ток I=50 А, расположена прямоугольная рамка, так что две ее большие стороны длиной l=65 см параллельны проводу, а расстояние от провода до ближайшей из этих сторон равно ее ширине. Каков магнитный поток Ф, пронизывающий рамку?
24. Тороид квадратного сечения содержит N=1000 витков. Наружный диаметр тороида D=40 см, внутренний d=20 см. Найти магнитный поток в тороиде, если сила тока, протекающего по обмотке, I=10 А.
 25. Найти магнитный поток через поперечное сечение тороида, если ток в обмотке I=1,7 А, полное число витков N=1000. Отношение внешнего диаметра к внутреннему h=1,6 и толщина h=5 см. Сердечник тороида прямоугольного сечения, магнитная проницаемость m=20.
25. Найти магнитный поток через поперечное сечение тороида, если ток в обмотке I=1,7 А, полное число витков N=1000. Отношение внешнего диаметра к внутреннему h=1,6 и толщина h=5 см. Сердечник тороида прямоугольного сечения, магнитная проницаемость m=20.
26. Ток I=10 А течет вдоль длинной тонкостенной трубы радиуса R=2 см, имеющей по всей длине продольную прорезь шириной b=2 мм. Найти магнитную индукцию:
а) внутри трубы;
б) в точке А на расстоянии d=2R (рис. 1.20).
27. Определить индукцию магнитного поля тока, равномерно распределенного по бесконечной плоскости с линейной плотностью  .
.
28. Постоянный ток течет по длинному прямому проводнику круглого сечения. Радиус провода R=5 мм. Плотность тока изменяется по сечению проводника по закону j=jor/R, jo=2×106А/м2. Найти поток вектора магнитной индукции через одну из половин осевого сечения в расчете на один метр его длины.
29. Определить индукцию магнитного поля тока, равномерно распределенного по двум бесконечным параллельным плоскостям с линейными плотностями  и
и  .
.
30. Длинный равномерно заряженный по объему цилиндр радиусом R=10 см приведен во вращение вокруг своей оси с угловой скоростью w=200 с-1. Объемная плотность заряда r=10-4 Кл/м3. Найти магнитную индукцию на оси цилиндра. Магнитную проницаемость всюду считать равной единице.
31. По длинному прямому проводнику в виде полой толстостенной трубки течет ток I=80 А. Внутренний и внешний радиусы равны соответственно R1=1 см и R2=2см. Найти индукцию магнитного поля этого тока как функцию расстояния r от оси проводника. Магнитную проницаемость всюду считать равной единице. Построить график В(r) для 0£ r £5 см.
32. Внутри длинного однородного прямого провода круглого сечения имеется круглая длинная цилиндрическая полость, ось которой параллельна оси провода и смещена относительно последней на расстояние  . По проводу течет постоянный ток плотности
. По проводу течет постоянный ток плотности 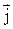 . Найти индукцию магнитного поля внутри полости.
. Найти индукцию магнитного поля внутри полости.
33. По объему однородного шара массы m и радиуса R равномерно распределен заряд q. Шар приводится во вращение вокруг своей оси с угловой скоростью ω. Найти возникающий в результате вращения магнитный момент рm.
 34. По прямому проводнику (рис. 1.21) в виде тонкой ленты шириной h=10 см течет ток I=32 А. Найти величину и направление индукции магнитного поля:
34. По прямому проводнику (рис. 1.21) в виде тонкой ленты шириной h=10 см течет ток I=32 А. Найти величину и направление индукции магнитного поля:
а) в точке А (а=5 см);
б) в точке В (а=5 см);
в) в точке С (а=5 см).
35. Постоянный ток протекает по длинному прямому проводнику круглого сечения. Радиус провода R=5 мм. Плотность тока в проводе изменяется по закону j=jo×(1-r/R), jo=1×106A/м2. Найти индукцию магнитного поля этого тока как функцию расстояния от оси провода, построить график В(r). Вычислить магнитную индукцию:
а) на расстоянии r=R/2;
б) на расстоянии r=2R.
36. Длинный прямой медный провод радиусом R=5 мм расположен по оси железной толстостенной трубы. Внутренний и внешний радиусы равны R1=10 мм и R2=15 мм соответственно. По медному проводу течет ток силой I=80 А. Найти магнитную индукцию как функцию расстояния r от оси системы. Построить график В=f(r).
37. Через центр железного кольца перпендикулярно его плоскости проходит длинный прямой провод, по которому течет ток I=25 А. Кольцо прямоугольного сечения с внутренним радиусом R1=18 мм, внешним R2=22 мм и толщиной h=5 мм. Считая приближенно, что в любой точке сечения кольца индукция одинакова и равна индукции на средней линии кольца, найти магнитный поток Ф, пронизывающий площадь сечения кольца.
38. Через центр железного кольца перпендикулярно его плоскости проходит длинный прямой провод, по которому течет ток I=25 А. Кольцо прямоугольного сечения с внутренним радиусом R1=16 мм, внешним R2=24 мм и толщиной h=5 мм. Считая приближенно, что в любой точке сечения кольца магнитная проницаемость одинакова и соответствует значению напряженности на средней линии кольца, найти магнитный поток Ф, пронизывающий площадь сечения кольца.
39. Замкнутый железный сердечник длиной L=50 см имеет обмотку из N=1000 витков. По обмотке течет ток I1=1 А. Какой ток I2 надо пропустить через обмотку, чтобы при удалении сердечника индукция внутри обмотки осталась прежней?
40. Сколько ампер-витков потребуется для создания магнитного потока Ф=0,42 мВб в соленоиде с железным сердечником длиной l=120 см и площадью поперечного сечения S=3 см2?
41. Длина железного сердечника тороида l1=2,5 м, длина поперечного воздушного зазора l2=1 см. Число витков в обмотке тороида N=1000. При токе I=20 А индукция магнитного поля в зазоре B=1,6 Тл. Найти магнитную проницаемость железного сердечника при этих условиях. (Зависимость В от Н для железа неизвестна.)
42. Найти магнитную индукцию В в замкнутом железном сердечнике тороида длиной l=20,9 см, если число ампер-витков обмотки тороида IN=1500 А×в. Какова магнитная проницаемость m материала сердечника при этих условиях?
43. Железное кольцо диаметром D=11,4 см имеет обмотку из N=200 витков, по которой течет ток I1=15 А. Какой ток I2 должен проходить по обмотке, чтобы индукция в сердечнике осталась прежней, если в кольце сделать зазор шириной b=1 мм? Найти магнитную проницаемость материала сердечника при этих условиях.
 44. Магнитная индукция в вакууме вблизи плоской границы магнетика равна В, и вектор
44. Магнитная индукция в вакууме вблизи плоской границы магнетика равна В, и вектор  составляет угол J с нормалью
составляет угол J с нормалью  к поверхности (рис. 1.22). Магнитная проницаемость магнетика равна m. Найти:
к поверхности (рис. 1.22). Магнитная проницаемость магнетика равна m. Найти:
а) поток вектора 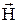 через поверхность сферы S радиусом R, центр которой лежит на поверхности магнетика (рис. 1.22, а);
через поверхность сферы S радиусом R, центр которой лежит на поверхности магнетика (рис. 1.22, а);
б) циркуляцию вектора  по квадратному контуру Г со стороной l (рис. 1.22, б);
по квадратному контуру Г со стороной l (рис. 1.22, б);
в) определить величину и направление вектора  в магнетике.
в магнетике.
Вычислить все величины для следующих значений: В=0,01 Тл, J=60о, m=10, R=10 см, l=10 см.
45. Постоянный магнит (железо) имеет вид кольца с узким зазором между полюсами. Средний диаметр кольца d=20 см. Ширина зазора b=2,0 мм. Магнитная индукция в зазоре B=40 мТл. Пренебрегая рассеянием магнитного потока на краях зазора, найти:
а) модуль вектора напряженности магнитного поля внутри магнита,
б) модуль вектора намагниченности  .
.
46. На железном сердечнике в виде тора со средним радиусом сердечника R=250 мм имеется обмотка с общим числом витков N=1000. В сердечнике сделана прорезь шириной b=1,0 мм. При токе I=0,85 А через обмотку магнитная индукция в зазоре B=0,75 Тл. Пренебрегая рассеянием магнитного потока на краях зазора, найти:
а) напряженность магнитного поля в сердечнике;
б) величину вектора намагниченности в сердечнике;
в) магнитную проницаемость железа в этих условиях.
47. Тонкое железное кольцо со средним диаметром d=50 см несет на себе обмотку из N=800 витков с током I=3,0 А. В кольце имеется поперечная прорезь шириной b=2,0 мм. Пренебрегая рассеянием магнитного потока на краях зазора, найти с помощью графика магнитную проницаемость железа в этих условиях.
48. Железный сердечник длиной l1=50,2 см с поперечным воздушным зазором шириной l2=0,1 см имеет обмотку из N=20 витков. Какой ток I должен протекать по этой обмотке, чтобы в зазоре получить магнитную индукцию B=1,2 Тл?
49. Между полюсами электромагнита требуется создать магнитное поле с индукцией В=1,4 Тл. Длина железного сердечника l1=40 см, длина межполюсного пространства l2=1 см, диаметр сердечника D=5 см. Какое напряжение нужно подать на обмотку электромагнита, чтобы получить требуемое магнитное поле, используя медную проволоку площадью поперечного сечения S=1 мм2? Какая при этом будет наименьшая толщина b намотки, если считать, что предельно допустимая плотность тока j=3 МА/м2?
50. Тороид с железным сердечником, длина которого по средней линии l=1м, имеет воздушный поперечный зазор шириной l2. По обмотке тороида, содержащей N=1300 витков, пустили ток I=2 A, в результате чего индукция в зазоре В2 стала равна 1 Тл. Определить ширину зазора l2.
51. Внутри соленоида длиной l=25,1 см и диаметром D=2 см помещён железный сердечник. Соленоид имеет N=200 витков. Определить магнитный поток Ф, если ток в соленоиде I=5 А.
52. Тороид намотан на железное кольцо сечением S=5 см2. При силе тока I=1 А магнитный поток через поперечное сечение кольца Ф=250 мкВб. Определить число витков тороида, приходящихся на отрезок длиной 1 см средней линии кольца.
53. Внутри соленоида с числом витков N=200 с никелевым сердечником (m=200) напряженность однородного магнитного поля H=10 кA/м. Площадь поперечного сечения сердечника S=10 см2. Определить: 1) магнитную индукцию поля внутри соленоида; 2) потокосцепление.
54. Тороид с железным сердечником, длина которого по средней линии l=1 м, имеет воздушный зазор l2=3 мм. По обмотке тороида, содержащей N=1300 витков, пустили ток, в результате чего индукция в зазоре В2 стала равна 1 Тл. Определить силу тока.
55. Индукция магнитного поля в вакууме вблизи плоской поверхности однородного изотропного магнетика равна В, причем вектор магнитной индукции составляет угол a с нормалью к поверхности. Магнитная проницаемость магнетика равна m. Найти модуль вектора индукции В¢ магнитного поля в магнетике вблизи поверхности.
56. Прямой бесконечно длинный проводник с током лежит в плоскости раздела двух непроводящих сред с магнитными проницаемостями m1 и m2. Найти модуль магнитной индукции во всем пространстве в зависимости от расстояния r от провода. Иметь в виду, что линии вектора магнитной индукции являются окружностями с центром на оси проводника.
57. Тороидальный сердечник составлен из двух половинок, сделанных из различных ферромагнитных материалов с магнитными проницаемостями m1 и m2 (рис. 1.23). Общая длина сердечников, включая два зазора размером l каждый, равна L. По об  мотке сердечника, имеющей N витков, течет ток I. Определить магнитную индукцию в зазоре.
мотке сердечника, имеющей N витков, течет ток I. Определить магнитную индукцию в зазоре.
58. Требуется построить электромагнит, который создает в зазоре магнитное поле с индукцией В=1 Тл. Длина железного сердечника l=140 см, ширина воздушного зазора d=1 см, диаметр сердечника D=6 см. Какое наименьшее число витков N должна иметь обмотка, если используется медный провод площадью сечения S=1мм2, по которому можно пропустить ток, не превышающий I=3 А? Определить напряжение U, которое нужно подать на обмотку для получения максимального поля. Принять магнитную проницаемость железа m=103.
59. Замкнутый тороид с железным сердечником имеет N=400 витков из тонкого провода, намотанных в один слой. Средний диаметр тороида d=25 см. Определить напряженность и индукцию магнитного поля внутри тороида, магнитную проницаемость m железа, а также намагниченность J при значениях силы тока в обмотке I1=0,5 А и I2=5 А.
60. Обмотка тороида, имеющего стальной сердечник с вакуумным поперечным зазором длиной l=3 мм, содержит n=1000 вит./м. Средний диаметр тороида d=30 см. При какой силе тока I в обмотке магнитная индукция в зазоре равна 1 Тл?
61. Постоянный магнит имеет форму тонкого диска, намагниченного вдоль его оси. Радиус диска R=1,0 см, толщина h=1 мм. Оценить значение молекулярного тока I', текущего по ободу диска, и намагниченность J материала диска (считая ее однородной), если магнитная индукция на оси диска в точке, отстоящей на х=10 см от его центра, составляет В=30 мкТл.
 62. В установке (рис. 1.24) измеряют с помощью весов силу, с которой парамагнитный шарик объема V=41 мм3 притягивается к полюсу электромагнита М. Индукция магнитного поля на оси полюсного наконечника зависит от высоты х как В=Воexp(-ax2), где Во=1,50 Тл, а=100 м-2. Найти магнитную восприимчивость парамагнетика, если максимальная сила притяжения Fмакс=160 мкН. Считать намагниченность сферического образца однородной.
62. В установке (рис. 1.24) измеряют с помощью весов силу, с которой парамагнитный шарик объема V=41 мм3 притягивается к полюсу электромагнита М. Индукция магнитного поля на оси полюсного наконечника зависит от высоты х как В=Воexp(-ax2), где Во=1,50 Тл, а=100 м-2. Найти магнитную восприимчивость парамагнетика, если максимальная сила притяжения Fмакс=160 мкН. Считать намагниченность сферического образца однородной.
63. Тороидальный чугунный сердечник со средним диаметром d=50 см несет на себе обмотку из N=800 витков. В сердечнике имеется поперечная прорезь шириной b=2,0 мм. Пренебрегая рассеянием магнитного потока на краях зазора, найти силу тока в обмотке, при которой магнитная индукция в зазоре В=1 Тл. Определить сечение медного провода обмотки, учитывая, что предельная плотность тока jпред =5 А/мм2.