ГРАВИТАЦИОННОЕ ПОЛЕ. ЕГО НАПРЯЖЕННОСТЬ И ПОТЕНЦИАЛ.

Гравитацио́нное по́ле, или по́ле тяготе́ния — физическое поле, через которое осуществляется гравитационное взаимодействие[1].

Гравитационное поле в классической физике

Классическая теория тяготения Ньютона

Закон тяготения Ньютона

В рамках классической физики гравитационное взаимодействие описывается «законом всемирного тяготения» Ньютона, согласно которому сила гравитационного притяжения между двумя материальными точками с массами и пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними:

Здесь — гравитационная постоянная, приблизительно равная м³/(кг с²), — расстояние между точками.

Для расчёта поля в более сложных случаях, когда тяготеющие массы нельзя считать материальными точками, можно воспользоваться тем фактом, что поле ньютоновского тяготения потенциально. Если обозначить плотность вещества ρ, то потенциал поля φ удовлетворяетуравнению Пуассона:

Недостатки ньютоновской модели тяготения

Практика показала, что классический закон всемирного тяготения позволяет с огромной точностью объяснить и предсказать движения небесных тел. Однако ньютоновская теория содержала ряд серьёзных недостатков. Главный из них — необъяснимое дальнодействие: сила притяжения передавалась неизвестно как через совершенно пустое пространство, причём бесконечно быстро. По существу ньютоновская модель была чисто математической, без какого-либо физического содержания. Кроме того, если Вселенная, как тогда предполагали, евклидова и бесконечна, и при этом средняя плотность вещества в ней ненулевая, то возникает гравитационный парадокс: потенциал поля всюду обращается в бесконечность. В конце XIX века обнаружилась ещё одна проблема: заметное расхождение теоретического и наблюдаемого смещения перигелия Меркурия.

На протяжении более двухсот лет после Ньютона физики предлагали различные пути усовершенствования ньютоновской теории тяготения. Эти усилия увенчались успехом в 1915 году, с созданием общей теории относительности Эйнштейна, в которой все указанные трудности были преодолены. Теория Ньютона оказалась приближением более общей теории, применимым при выполнении двух условий:

Гравитационный потенциал в исследуемой системе не слишком велик (много меньше ).

Скорости движения в этой системе незначительны по сравнению со скоростью света.

 

Напряжённость гравитацио́нного по́ля — векторная величина, характеризующая гравитационное поле в данной точке и численно равная отношению силы тяготения, действующей на тело, помещённое в данную точку поля, к гравитационной массе этого тела:

Свойства

Если источником гравитационного поля является некое гравитирующее тело, то согласно закону всемирного тяготения:

где:

— гравитационная постоянная;

— гравитационная масса тела-источника поля;

— расстояние от исследуемой точки пространства до центра масс тела-источника поля.

Применяя второй закон Ньютона и принцип эквивалентности гравитационной и инерционной масс:

то есть напряжённость гравитационного поля численно (и по размерности) равна ускорению свободного падения в этом поле.

Гравитацио́нный потенциа́л — скалярная функция координат и времени, характеризующая гравитационное поле в классической механике. Имеет размерность квадрата скорости, обычно обозначается буквой 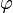. Гравитационный потенциал равен отношению потенциальной энергии материальной точки, помещённой в рассматриваемую точку гравитационного поля, к массе этой точки. Впервые понятие гравитационного потенциала ввёл в науку Адриен Мари Лежандр в конце XVIII века.

 

Гравитационный потенциал и уравнения движения[править | править исходный текст]

Движение частицы в гравитационном поле в классической механике определяется функцией Лагранжа, имеющей в инерциальной системе отсчета вид:

, где: — масса частицы, — координата частицы, 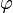— потенциал гравитационного поля.

Подставляя выражение для лагранжиана L в уравнения Лагранжа:

,

получаем уравнения движения

.