Сосредоточенные силы и распределенные нагрузки
До сих пор в системе мы рассматривали силы, приложенные к твердому телу в какой-либо его точке. Такие силы называются сосредоточенными.
Однако в инженерных расчетах часто приходится встречаться с нагрузками, распределенными вдоль данной поверхности или линии по тому или иному закону. Распределенные силы прежде всего характеризуются интенсивностью q, т.е. величиной силы, приходящейся на единицу поверхности или линии.
Так как все аксиомы и теоремы статики получены для сосредоточенных сил, то необходимо рассмотреть способы перехода от распределенных сил к сосредоточенным в простейших, часто возникающих случаях.
1)Силы, равномерно распределенные вдоль отрезка прямой (рис.5.4).
 |
Рис.5.4.
Понятно, что q-здесь величина постоянная. При статических расчетах эту систему сил можно заменить сосредоточенной силой (ее равнодействующей), которая по модулю равна
Q=q×a
и приложена в ее середине.
2)Силы, равномерно распределенные вдоль отрезка прямой по линейному закону (рис.5.5). Например, силы давления воды на плотину, которые имеют наибольшее давление у дна и равны нулю у поверхности воды. Здесь q-величина переменная, принимающая значения 0£q£qmax.
 |
Рис.5.5.
Равнодействующая такой распределенной нагрузки по модулю равна
Q=  aqmax,
aqmax,
а ее линия действия проходит через центр тяжести треугольника АВС, который находится в точке пересечения медиан, т.е. линия действия силы Q проходит на расстоянии 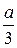 от стороны ВС треугольника АВС.
от стороны ВС треугольника АВС.
3)Силы, равномерно распределенные по дуге окружности (рис.5.6)
 |
Рис.5.6.
Примером таких сил могут служить силы гидростатического давления на боковые стенки цилиндра.
Равнодействующая таких сил по модулю равна
Q=q×h,
где h-длина хорды, стягивающей дугу АВ. Направлена сила 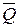 по оси симметрии дуги окружности.
по оси симметрии дуги окружности.
В заключение в качестве примера рассмотрим еще один вид связи - жесткую заделку конца балки (рис.5.7).
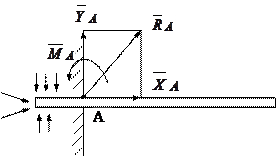 |
Рис.5.7.
Такая опора не допускает не только линейных перемещений балки, но и ее поворота. На заделанную часть действуют со стороны стены неравномерно распределенные силы. Пользуясь леммой о параллельном переносе силы, их можно привести к точке А и заменить одной силой  и одной парой с моментом MA. Нахождение неизвестной по модулю и направлению реакции
и одной парой с моментом MA. Нахождение неизвестной по модулю и направлению реакции  в свою очередь можно заменить нахождением двух ее составляющих
в свою очередь можно заменить нахождением двух ее составляющих  , направленным по осям координат. Следовательно, реакция жесткой заделки состоит из трёх неизвестных величин
, направленным по осям координат. Следовательно, реакция жесткой заделки состоит из трёх неизвестных величин  , MA.
, MA.