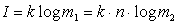Количество информации, как мера снятой неопределенности

При передаче сообщений, о какой либо системе происходит уменьшение неопределенности. Если о системе все известно, то нет смысла посылать сообщение. Например, если мы получим сообщение, что Париж - столица Франции, то мы не получим никакой информации - это нам и так известно. Но если мы получаем сведения о системе для нас неизвестной, то получим соответствующее количество информации. И чем более неопределенным было состояние системы, тем большее количество информации мы получим. Поэтому количество информации измеряют уменьшением энтропии.

Рассмотрим систему Х над которой производится наблюдение. Допустим, что мы получили полную информацию о системе Х. Пусть до наблюдения энтропия системы равнялась H. В результате наблюдения энтропия равна нулю H=0, то есть все о системе известно. Тогда информация будет равна уменьшению энтропии: I=H-0, I=H.

То есть, количество информации, приобретаемое при полном выяснении состояния некоторой физической системы, равно энтропии этой системы: 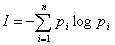. Количество информации I - есть осредненное значение логарифма вероятности состояния. Тогда каждое отдельное слагаемое -log p_i необходимо рассматривать как частную информацию, получаемую от отдельного сообщения, то есть . Полная информация будет представлять математическое ожидание от частных значений . 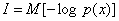Если все возможные состояния системы априори одинаково вероятны p₁=p₂= . . . =p_n=1/n , то I_i= -log p_i=log n. Частная информация равна средней (полной) информации.

В случае если состояния системы обладают различными вероятностями, информация от разных сообщений неодинакова: наибольшую информацию несут сообщения о тех событиях, которые априори были наименее вероятны. Например, сообщение о том, что 31 декабря в Казани выпал снег, несет гораздо меньше информации, чем аналогичное сообщение, что 31 июля выпал снег.

Пример 1. Допустим, что нам интересно знать, сдал или не сдал экзамен некий студент Петров. Примем следующие вероятности этих двух событий: p(сдал)=7/8, p(не сдал)=1/8. Отсюда видно, что этот студент является довольно сильным. И сообщение, что он сдал экзамен, несет мало информации. . При сообщении, что не сдал, мы удивимся: ”Неужели?” .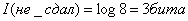

Пример 2. Тексты, составленные из 32 букв алфавита, передаются по телетайпу при помощи двух качественных признаков (1 и 0). Чему равно количество информации, приходящееся на одну принятую букву, на k принятых букв.

Решение. m₁ - число букв первичного алфавита, m_{2 -} число символов вторичного алфавита. Для передачи 32 букв необходимо 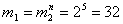, их следует комбинировать по 5 символов, откуда n=5. .

Количество информации на букву относительно первичного алфавита: . Количество информации на букву относительно вторичного алфавита: Количество информации на k принятых букв: