Лекция №2 «Нормальные напряжения при чистом изгибе. Закон Гука при изгибе. Условие прочности при изгибе».

 

Основной метод для определения внутренних силовых факторов в сопротивлении материалов – метод сечений. Он дает возможность определить поперечную силу и изгибающий момент. Каким образом распределяются напряжения по сечению балки при изгибе? Эту задачу можно решить, рассматривая деформации. При рассмотрении деформации растяжения-сжатия было установлено, что все волокна материала получают в направлении действия сил одинаковые относительные деформации. Следовательно, нормальные напряжения при растяжении-сжатии распределяются равномерно. Установим, каким образом распределяются напряжения по сечению при чистом изгибе с помощью деформаций.

Возьмём часть балки, изгибаемую двумя равными и противоположно направленными моментами.

M N – нейтральный слой. Нейтральный слой не сжимается и не растягивается, он искривляется. Кривизной нейтрального слоя называется величина, обратная радиусу кривизны , размерность , - радиус кривизны.

Точка О общий центр кривизны. Выделим элемент бруса между двумя сечениями (1 и 2).

Нейтральные волокна не изменили размера, а волокна на расстоянии у удлинились.

dS – длина нейтрального волокна

 

- абсолютное удлинение растянутого слоя.

 

Из подобия треугольников и можно записать следующее соотношение:

 

-отношение абсолютного удлинения к первоначальной длине равно относительной деформации , следовательно ,

это значит - относительная деформация прямо пропорциональна расстоянию от нейтрального слоя и обратно пропорциональна радиусу кривизны.

Так как волокна бруса при изгибе испытывают только простое растяжение или сжатие, то для определения распределения напряжений по сечению можно применить закон Гука при растяжении-сжатии.

 

По этой формуле можно выяснить, что распределение напряжений по сечению зависит от y .

При y=0 (нейтральный слой) 0

Максимальные напряжения будут в точке, для которой расстояние y наибольшее, т. е. на поверхности балки.

При отрицательном значении y меняется знак нормальных напряжений. Нормальные напряжения будут отрицательные.

Рассчитать нормальные напряжения по формуле невозможно, так как неизвестен радиус кривизны . Значит нужно перейти к известным величинам, к изгибающему моменту .

dМ – элементарный момент – момент, действующий на элементарную площадку. Равный произведению элементарной нормальной силы dN на плечо y.

 

,

 

 

Просуммируем (проинтегрируем) все элементарные моменты dМ по всему сечению, получим , приложенный к сечению:

 

 

 

- изгибающий момент, берётся максимальное значение с эпюры изгибающего момента.

Таким образом, можно определить неизвестную величину

 

- закон Гука при изгибе

 

Кривизна нейтрального слоя прямо пропорциональна изгибающему моменту и обратно пропорциональна произведению модуля Юнга на осевой момент инерции сечения - жёсткость сечения при изгибе.

Вычислим значение напряжения в любой точке сечения

 

Нормальные напряжения в любой точке сечения прямо пропорциональны изгибающему моменту, расстоянию до нейтрального слоя и обратно пропорциональны осевому моменту инерции сечения.

Наибольшие нормальные напряжения на поверхности, при значении y=h/2

 

- момент сопротивления изгибу.

 

- момент сопротивления изгибу для прямоугольного сечения, геометрическая характеристика балки.

Условие прочности при изгибе:

 

 

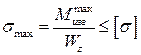
Максимальные напряжения меньше или равны допускаемым. Прочность обеспечена.

 

При изгибе нейтральный слой проходит через центр тяжести сечения.

Для этого рассмотрим продольную силу, действующую в любом сечении, которая по условию равновесия равна сумме внешних сил, действующих на отсечённую часть балки.

 

Так как все силы упругости, действующие в сечении, равны внешним, при этом сумма всех внешних сил в проекциях на ось оx равна нулю (два внешних момента, созданные из системы двух равных и противоположно направленных сил, равны и противоположно направлены).

Значит

Заменим сумму на интеграл

 

Из всех слагаемых, входящих в данную формулу только статический момент площади сечения 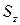может равняться нулю, когда нейтральная ось проходит через центр тяжести сечения.

Это означает, что нейтральная ось проходит через центр тяжести сечения.