Миноры и алгебраические дополнения

Определение. Если в определителе n-го порядка выбрать произвольно k строк и k столбцов, то элементы, стоящие на пересечении указанных строк и столбцов, образуют квадратную матрицу порядка k. Определитель такой квадратной матрицы называют минором k-го порядка.

Обозначается M_k . Если k=1, то минор первого порядка - это элемент определителя.

Элементы, стоящие на пересечении оставшихся (n-k) строк и (n-k) столбцов, составляют квадратную матрицу порядка (n-k). Определитель такой матрицы называется минором, дополнительнымк минору M_k. Обозначается M_n-k.

Алгебраическим дополнением минора M_k будем называть его дополнительный минор, взятый со знаком “+” или “-” в зависимости от того, четна или нечетна сумма номеров всех строк и столбцов, в которых расположен минор M_k.

Если k=1, то алгебраическое дополнение к элементу a_ik вычисляется по формуле

A_ik=(-1)^i+kM_ik, где M_ik - минор (n-1) порядка.

Теорема. Произведение минора k-го порядка на его алгебраическое дополнение равно сумме некоторого числа членов определителя D_n.

Доказательство

1. Рассмотрим частный случай. Пусть минор M_k занимает левый верхний угол определителя, то есть располагается в строках с номерами 1, 2, ..., k, тогда минор M_n-k будет занимать строки k+1, k+2, ..., n.

.

Вычислим алгебраическое дополнение к минору M_k. По определению,

A_n-k=(-1)^sM_n-k, где s=(1+2+...+k) +(1+2+...+k)= 2(1+2+...+k), тогда

(-1)^s=1 и A_n-k=M_n-k. Получим

M_k A_n-k=M_k M_n-k. (*)

Берем произвольный член минора M_k

, (1)

где s - число инверсий в подстановке

(2)

и произвольный член минора M_n-k

, (3)

где s^* - число инверсий в подстановке

(4)

Перемножая (1) и (3), получим

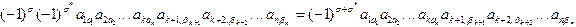.(5)

Произведение состоит из n элементов, расположенных в различных строках и столбцах определителя D. Следовательно, это произведение является членом определителя D. Знак произведения (5) определяется суммой инверсий в подстановках (2) и (4), а знак аналогичного произведения в определителе D определяется числом инверсий s_k в подстановке

Очевидно, что s_k=s+s^*.

Таким образом, возвращаясь к равенству (*), получим, что произведение M_k A_n-k состоит только из членов определителя.

2. Пусть минор M_k расположен в строках с номерами i₁, i₂, ..., i_k и в столбцах с номерами j₁, j₂, ..., j_k , причем i₁< i₂< ...< i_k и j₁< j₂< ...< j_k .

Используя свойства определителей, с помощью транспозиций сместим минор в левый верхний угол. Получим определитель D^¢, в котором минор M_k занимает левый верхний угол, а дополнительный к нему минор M¢_n-k - правый нижний угол, тогда, по доказанному в пункте 1, получим, что произведение M_k M¢_n-k является суммой некоторого количества элементов определителя D^¢, взятых со своим знаком. Но D^¢ получен из D с помощью (i₁-1)+( i₂-2)+ ...+(i_k-k)=( i₁+ i₂+ ...+ i_k)-(1+2+...+k) транспозиций строк и (j₁-1)+(j₂-2)+ ...+(j_k-k)=(j₁+ j₂+ ...+ j_k)- (1+2+...+k) транспозиций столбцов. То есть всего было выполнено

( i₁+ i₂+ ...+ i_k)-( 1+2+...+k)+ (j₁+ j₂+ ...+ j_k)- (1+2+...+k)= ( i₁+ i₂+ ...+ i_k)+ (j₁+ j₂+ ...+ j_k)- 2(1+2+...+k)=s-2(1+2+...+k). Поэтому члены определителей D и D^¢ отличаются знаком (-1)^{s-2(1+2+...+k)}=(-1)^s, следовательно, произведение (-1)^s M_k M¢_n-k будет состоять из некоторого количества членов определителя D, взятых с теми же знаками, какие они имеют в этом определителе.

Теорема Лапласа. Если в определителе n-го порядка выбрать произвольно k строк (или k столбцов) 1£k£n-1, тогда сумма произведений всех миноров k-го порядка, содержащихся в выбранных строках, на их алгебраические дополнения равна определителю D.

Доказательство

Выберем произвольно строки i₁, i₂, ..., i_k и докажем, что

.

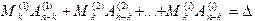Ранее было доказано, что все элементы в левой части равенства содержатся в качестве слагаемых в определителе D. Покажем, что каждый член определителя D попадает только в одно из слагаемых . Действительно, всякое t_s имеет вид t_s= 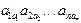. если в этом произведении отметить сомножители, у которых первые индексы i₁, i₂, ..., i_k, и составить их произведение , то можно заметить, что полученное произведение принадлежит минору k-го порядка. Следовательно, оставшиеся члены, взятые из оставшихся n-k строк и n-k столбцов, образуют элемент, принадлежащий дополнительному минору, а с учетом знака - алгебраическому дополнению, следовательно, любое t_s попадает только в одно из произведений , что доказывает теорему.

Следствие (теорема о разложении определителя по строке). Сумма произведений элементов некоторой строки определителя на соответствующие алгебраические дополнения равна определителю.

(Доказательство в качестве упражнения.)

Теорема. Сумма произведений элементов i-ой строки определителя на соответствующие алгебраические дополнения к элементам j-ой строки (i¹j) равна 0.

(Доказательство в качестве упражнения.)

Таким образом, мы получили формулы

Аналогично

Пример 1. Вычислить определитель по теореме Лапласа (предварительно разложив его по 2 и 3 строкам).

= =

=(4+3)(-9-0) - (8-3)(0-20) + (12-6)(0-15) + (-4-2)(-3-16) - (-6-4)(0-12) + (6-8)(5-0)= = -63+100-90+114-120-10=-69.

Пример 2. Вычислить определитель, разложив его по последнему столбцу.

7

-7(25 + 0 + 16 + 12 - 60 - 0) + 3(50 + 0 - 24 + 16 - 0 + 90) - (100 + 0 + 24 + 32 - 0 + 75) + 4(-40 + 20 - 54 - 48 - 30 - 30) = 49 + 396 - 231 - 182 = 32.

Замечание. Удобно применять следствие из теоремы Лапласа к определителю, преобразованному с помощью свойств таким образом, что в одной из строк (или в одном из столбцов) все элементы, кроме одного, равны 0.

Пример. Вычислить определитель

-12 -14 +35 -147 -20 -2= -160.