КОНСТРУКТИВНЫЕ ЛОГИКИ
Еще в 1908 г. голландский аспирант (Э.Л.Я. Брауэр опубликовал на голландском языке диссертацию под наглым названием: «De onbetrouwbaarheid der logische principes», что означает «Недостоверность логических принципов». Брауэр аргументировал, что причина тех неприятностей, с которыми столкнулась математика в начале XX века (и которые не преодолены и до сих пор; к ним просто привыкли и стали игнорировать), не в каких-то частных принципах теории множеств, а в самой логике[5].
Логика создавалась для конечных объектов, а перенесли её на бесконечные. В частности, для бесконечных объектов нельзя считать автоматически выполненным закон исключенного третьего « или не » (на символическом языке современной логики 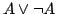 ), поскольку мы можем просто не уметь распознать эти два случая. Брауэр показал, что закон исключенного третьего в обычной логике эквивалентен ещё одному общепринятому закону: снятия двойного отрицания
), поскольку мы можем просто не уметь распознать эти два случая. Брауэр показал, что закон исключенного третьего в обычной логике эквивалентен ещё одному общепринятому закону: снятия двойного отрицания 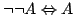 , который в курсе математики выступает в качестве доказательств от противного: «Нужно доказать A . Предположим, что не верно A … Получаем абсурд. Полученное противоречие доказывает теорему» Как всегда у первооткрывателей, гениальные прозрения у Брауэра сочетались с некорректными объяснениями. Если причина недоразумений в самой логике, почему же эллины, создавшие и отработавшие классическую логику на примере геометрии, в которой также рассматривается бесконечная совокупность объектов, ни с какими неприятностями, проистекающими от нее, не сталкивались? Да дело просто в том, что гениальная интуиция и потрясающее чувство гармонии эллинов воспрепятствовали им использовать в геометрии числа. Тем самым они избежали попадания в область неразрешимых проблем. А, как показал Гёдель, там, где появляются натуральные числа, возникают и неразрешимые проблемы. Но, конечно же, неразрешимые проблемы возникают лишь для бесконечных совокупностей объектов. А там, где возникают неразрешимые проблемы, закон исключенного третьего выглядит до глупости оптимистичным: как мы можем утверждать, что или не, когда мы в принципе не можем знать ни того, ни другого? Но самое важное у Брауэра было то, что он полностью видоизменил приоритеты математики[6].
, который в курсе математики выступает в качестве доказательств от противного: «Нужно доказать A . Предположим, что не верно A … Получаем абсурд. Полученное противоречие доказывает теорему» Как всегда у первооткрывателей, гениальные прозрения у Брауэра сочетались с некорректными объяснениями. Если причина недоразумений в самой логике, почему же эллины, создавшие и отработавшие классическую логику на примере геометрии, в которой также рассматривается бесконечная совокупность объектов, ни с какими неприятностями, проистекающими от нее, не сталкивались? Да дело просто в том, что гениальная интуиция и потрясающее чувство гармонии эллинов воспрепятствовали им использовать в геометрии числа. Тем самым они избежали попадания в область неразрешимых проблем. А, как показал Гёдель, там, где появляются натуральные числа, возникают и неразрешимые проблемы. Но, конечно же, неразрешимые проблемы возникают лишь для бесконечных совокупностей объектов. А там, где возникают неразрешимые проблемы, закон исключенного третьего выглядит до глупости оптимистичным: как мы можем утверждать, что или не, когда мы в принципе не можем знать ни того, ни другого? Но самое важное у Брауэра было то, что он полностью видоизменил приоритеты математики[6].
Если традиционная математика занимается поиском и доказательством теорем, то он начал её рассматривать как источник построений. Мало доказать теорему, нужно, чтобы обоснование дало нам построение объекта, существование которого утверждается в теореме. А использование доказательств в качестве источника построений — именно то, что нужно от математики информатику .
Конструктивная логика - раздел математической логики, изучающий рассуждения о конструктивных объектах и конструкциях. При таком понимании конструктивная логика шире, чем логика конструктивной математики. Самое заметное отличие от традиционной (классической) логики состоит в отсутствии исключенного третьего закона 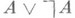 и двойного отрицания закона
и двойного отрицания закона 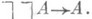
При обозначении систем чистой логики (исчисление высказываний, предикатов) термины "конструктивное", "интуиционистское", "гейтинговское" часто считаются синонимами (см. Рейтинга формальная система). Под конструктивной арифметикой иногда понимают гейтпнговскую арифметику, а иногда - ее расширение, получаемое добавлением принципа Маркова и схемы 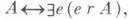 выражающей эквивалентность формулы и утверждения о ее реализуемости. Эта расширенная система, достаточная для доказательства основных результатов конструктивного математического анализа, не является, в отличие от гейтинговских систем, подсистемой классической арифметики: в ней опровергается закон исключенного
выражающей эквивалентность формулы и утверждения о ее реализуемости. Эта расширенная система, достаточная для доказательства основных результатов конструктивного математического анализа, не является, в отличие от гейтинговских систем, подсистемой классической арифметики: в ней опровергается закон исключенного  Иногда к конструктивной логике относят системы интуиционистской логики, содержащие средства описания специфически интуиционистских понятий. Общая черта подавляющего большинства систем К. л., отражающая специфику конструктивного понимания связки
Иногда к конструктивной логике относят системы интуиционистской логики, содержащие средства описания специфически интуиционистских понятий. Общая черта подавляющего большинства систем К. л., отражающая специфику конструктивного понимания связки 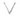 и квантора
и квантора 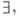 - явная реализация этих связок: выводимость
- явная реализация этих связок: выводимость 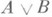 (соответственно существование хА (х)) влечет выводимость одной из формул А, В (соответственно A(t) для некоторого терма t). При этом в случае прикладных систем (арифметика, анализ) требуется замкнутость рассматриваемых формул. Большинство систем К. л. (включая все гейтинговские системы) корректны относительно различных понятий реализуемости, включая реализуемость по Клини и Гёделя интерпретацию: все выводимые формулы реализуемы, в частности истинны, в конструктивной семантике. С другой стороны, формальные системы К. л. обычно неполны относительно естественной конструктивной семантики. Для систем, содержащих арифметику, это следует из Гёделя теоремы о неполноте.
(соответственно существование хА (х)) влечет выводимость одной из формул А, В (соответственно A(t) для некоторого терма t). При этом в случае прикладных систем (арифметика, анализ) требуется замкнутость рассматриваемых формул. Большинство систем К. л. (включая все гейтинговские системы) корректны относительно различных понятий реализуемости, включая реализуемость по Клини и Гёделя интерпретацию: все выводимые формулы реализуемы, в частности истинны, в конструктивной семантике. С другой стороны, формальные системы К. л. обычно неполны относительно естественной конструктивной семантики. Для систем, содержащих арифметику, это следует из Гёделя теоремы о неполноте.
Множество реализуемых предикатных формул неперечислимо, поэтому конструктивное исчисление предикатов неполно относительно реализуемости, а из его полноты относительно "наивной" конструктивной семантики следовала бы интуиционистская истинность принципа 'конструктивного подбора. Конструктивное исчисление высказываний также неполно относительно реализуемости, но полно при некоторой интерпретации в терминах систем Поста. Арифметическая полуформальная система, полная относительно конструктивной семантики Маркова - Шанина, получается, если добавить к формальной конструктивной арифметике со схемой 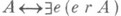 и принципом конструктивного подбора эффективное w-правило: из А(0), А(1), . . . вывести
и принципом конструктивного подбора эффективное w-правило: из А(0), А(1), . . . вывести 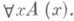 Для гейгинговских систем установлены теоремы полноты относительно теоретико-модельных семантик Крипке и Бета, использующих "возможные миры" (эти семантики связаны с теоретико-множественным вынуждением), а также относительно алгебраических и топологических моделей.
Для гейгинговских систем установлены теоремы полноты относительно теоретико-модельных семантик Крипке и Бета, использующих "возможные миры" (эти семантики связаны с теоретико-множественным вынуждением), а также относительно алгебраических и топологических моделей.
Классические формальные системы обычно погружаются в соответствующие системы конструктивной логики (с сохранением отношения выводимости из гипотез) с помощью негативного перевода, т. е. приписывания двойного отрицания 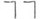 перед всеми подформулами. Поэтому системы арифметики, анализа и типов теории, основанные на классической логике, изоморфно вкладываются в соответствующие системы, основанные на конструктивной логике. Имеются системы теории множеств, основанные на К. л., в которые погружаются классические системы. Гейтинговские системы погружаются в модельные расширения классических с помощью d-перевода, т. е. приписывания знака необходимости D перед всеми подформулами. При этом D можно читать "доказуемо".
перед всеми подформулами. Поэтому системы арифметики, анализа и типов теории, основанные на классической логике, изоморфно вкладываются в соответствующие системы, основанные на конструктивной логике. Имеются системы теории множеств, основанные на К. л., в которые погружаются классические системы. Гейтинговские системы погружаются в модельные расширения классических с помощью d-перевода, т. е. приписывания знака необходимости D перед всеми подформулами. При этом D можно читать "доказуемо".
В некоторых системах К. л. справедливы суждения, ложные при классическом истолковании, например, отрицание закона исключенного третьего или специфически интуиционистские утверждения о последовательностях. Такие системы S сводятся к классическим системам 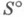 с помощью подходящего понятия реализуемости р. Доказывают, что
с помощью подходящего понятия реализуемости р. Доказывают, что  влечет существование t такого, что
влечет существование t такого, что 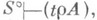 причем если А- числовое равенство, то
причем если А- числовое равенство, то 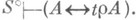 Отсюда следует непротиворечивость S относительно
Отсюда следует непротиворечивость S относительно 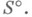
Конструктивная логика исследует истинность суждений также в нетрадиционных языках, отличных от языков логики предикатов арифметики, анализа и т. д. Наряду с традиционным отрицанием 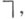 основанным на приведении к противоречию, изучается сильное отрицание
основанным на приведении к противоречию, изучается сильное отрицание 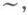 предусматривающее построение контрпримера. Для
предусматривающее построение контрпримера. Для  справедливы многие из законов классической логики, например.
справедливы многие из законов классической логики, например.

но теорема об эквивалентной замене верна лишь в виде
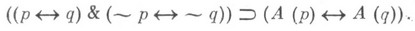
К системе сильного отрицания близки системы, основанные на симметричной трактовке истинности и ложности. Семантика для них предусматривает указание не только вида конструкций, обосновывающих истинность, но и вида конструкций, обосновывающих ложность рассматриваемого суждения.
Безотрицательная логика Грисса - Нельсона стремится избежать использования отрицания и ограничить класс свойств, о которых делаются утверждения, такими, для которых уже построены объекты, удовлетворяющие этим свойствам. Язык такой логики содержит связку 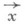 причем
причем 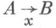 понимается приблизительно как
понимается приблизительно как 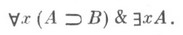
В теории конструкций исследуются сами правила построения и доказательства, лежащие в основе конструктивной математики. Конструкции строятся из исходных с помощью фиксированного набора комбинаторов и операции применения функции к аргументу. Формулы строятся из равенства с помощью связок логики высказываний и предиката доказуемости я, причем p(a, х-a(х)) читается "а есть доказательство того, что a(х) верно для всех x". В качестве аксиом берутся, в частности, все классические тавтологии (включая закон исключенного третьего), т. е. отношение "быть доказательством" предполагается разрешимым. Имеется корректная и точная интерпретация гейтинговских систем в теории конструкции.
Рассмотрение в конструктивной логике бескванторных систем вызвано стремлением получить финитные (в том или ином смысле) доказательства рассматриваемых суждений или их мажорант. Многие традиционные системы SК. л. погружаются в бескванторные системы S~ таким образом, что выводимость в S-суждения 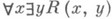 с бескванторной формулой R влечет выводимость в S-формулы R(x,j(х)). для подходящего j. Если S- арифметика без индукции, то S-примитивно рекурсивная арифметика; если S- гейтинговская арифметика, то S- - система гёделевских примитивно рекурсивных функционалов.
с бескванторной формулой R влечет выводимость в S-формулы R(x,j(х)). для подходящего j. Если S- арифметика без индукции, то S-примитивно рекурсивная арифметика; если S- гейтинговская арифметика, то S- - система гёделевских примитивно рекурсивных функционалов.
Для формальных систем конструктивной логики доказаны теоремы нормализации: любой вывод может быть конечным числом стандартных преобразований (редукций) приведен к нормальной форме, не содержащей "лишних" участков. Нормальные выводы обладают (в полной мере или, в случае арифметики и более широких систем, частично) свойством подформульности.
Имеются связи между конструктивной логикой и теорией категорий. Так, понятию "декартовой замкнутой категории" соответствует гейтинговское исчисление высказываний.
Иногда к конструктивной логике относят все логические рассмотрения, в которых требуется, чтобы все изучаемые объекты были конструктивными, независимо от применяемой логики. С этой тенденцией связано название конструктивных по Гёделю множеств.