Гидравлические потери

Потери напора возникают при движении реальной жидкости в результате работы сил трения. Различают потери на трение по длине (линейные потери), возникающие на прямых участках трубопровода и местные потери, которые имеют место на коротких участках трубопроводах при резкой его деформации.

Потери напора по длине h_л при движении жидкости в напорном трубопроводе определяются общей формулой Дарси–Вейсбаха:

 

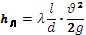, (3.31)

 

где λ − безразмерный коэффициент гидравлического трения (коэффициент Дарси);

l - длина трубопровода, м;

d - диаметр трубопровода, м;

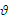- средняя скорость движения жидкости, м/с.

В общем случае коэффициент гидравлического трения λ зависит от режимов движения жидкости и относительной шероховатости, т.е. λ = f (Re, ).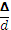

При разных режимах течения жидкости в трубе влияние этих величин проявляется по-разному (рассмотрено в пункте 3.5).

 

Местные потери выражают формулой Вейсбаха:

 

(3.32)

 

где 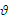– средняя скорость потока в сечении перед местным сопротивлением (расширение), или за ним (при сужении) и в тех случаях, когда рассматриваются поте­ри напора в гидроарматуре различного назначения, м/с;

ξ_м – безразмерный коэффициент местного сопротивления.

Числовое значение коэффициента местного сопротивления в основном определяется формой местного сопротивления, его геометрическими параметрами.

Можно считать, что при турбулентном режиме коэффициент местных сопротивлений ξ от числа Рейнольдса не зависит и, следовательно, как видно из формулы (3.32), потеря напора пропорциональна квадрату скорости (квадратичный режим сопро­тивления).

При ламинарном режиме считают, что

 

(3.33)

 

где А – коэффициент, определяемый формой местного сопротивления;

ξ_кв – коэффициент местного сопротивления при режиме квадратичного сопротивления, т.е. при .

При турбулентном режиме в случае внезапного расширения трубы потери напора определяется формулой Борда:

 

(3.34)

 

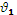где и 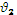− скорости до и после расширения потока;

− коэффициент сопротивления, равный для данного случая:

 

(3.35)

 

где S₁ и S₂ − площади сечений трубы до и после внезапного расширения, м².

При внезапном сужении трубы коэффициент сопротивления определяют по полуэмпирической формуле Идельчика:

 

(3.36)

 

Коэффициенты сопротивления для постепенно расширяющихся (конических труб) − диффузоров, плавно сужающихся труб − сопл, поворотов и других, более сложных местных гидравлических сопротивлений (кранов, клапанов, сеток, фильтров), приведены в справочной литературе.