Модели кривых роста

Для выявления тенденции развития используется распространенный прием сглаживания временного ряда, т.е. очистки временного ряда от искажающих эту тенденцию случайных отклонений. При этом методы сглаживания можно условно разделить на две группы: аналитические, основанные на известном виде функции, описывающей неслучайную компоненту; алгоритмические − не предполагающие точного знания вида функции f_i и задающие только алгоритм определения значений этой функции в заданной точке i. К первому классу относятся рассматриваемые в текущем разделе модели кривых роста, ко второму – метод скользящих средних, которому посвящен следующий раздел.

Простейшим приемом выявления тенденции является укрупнение интервалов, состоящее в замене данных, имеющих отношение к мелким временным периодам, данными по более крупным периодам. Например, можно заменить суточные данные недельными или декадными, декадные - месячными. Это позволит более отчетливо показать «ось развития явления».

Например, объем продажи валюты на биржах меняется изо дня в день под влиянием самых разнообразных факторов, включая и чисто случайные. Относительно меньшую колеблемость обнаруживают недельные объемы продажи валюты, еще меньшую - месячные и далее квартальные. Объединив мелкие интервалы в крупные, мы погасим часть случайной колеблемости и получим возможность более отчетливо показать основное направление развития событий на валютных биржах.

Недостатком этого приема является то, что с переходом к более крупным интервалам длина ряда сильно укорачивается. Поэтому, имея очень короткий ряд, выявить с его помощью какую-либо тенденцию развития невозможно. Таким образом, применение этого приема приходится ограничить лишь теми случаями, когда исходный временной ряд достаточно длинен. Когда, например, имеются данные не за одну неделю или декаду, а за все рабочие дни месяца или квартала.

Кривые роста, описывающие закономерности развития явлений во времени, получают путем аналитического выравнивания динамических рядов. Выравнивание ряда с помощью тех или иных функций в большинстве случаев оказывается удобным средством описания эмпирических данных, характеризующих развитие во времени исследуемого явления. Это средство удобно и для прогнозирования.

Суть метода кривых роста состоит в аппроксимации (приближении) значений наблюдаемого показателя некоторой функцией (кривой роста), содержащей неизвестные параметры, которые находятся по имеющемуся ряду значений показателя. Прогноз выполняется путем нахождения значения полученной функции в соответствующей точке.

Процесс разработки прогноза с использованием кривых роста состоит из следующих основных этапов:

· выбор типа кривой, форма которой соответствует характеру изменения динамического ряда;

· идентификация числовых значений (оценивание) параметров кривой;

· проверка адекватности выбранной кривой и оценка точности модели;

· расчет прогноза.

Задача выбора типа кривой является основной при выравнивании ряда. При всех прочих равных условиях ошибка в решении этого вопроса оказывается более значимой по своим последствиям, чем ошибка, связанная со статистическим оцениванием параметров.

Для выравнивания динамических рядов наиболее часто применяются следующие группы функций, большинство из которых может быть сведено к линейным[2]: I) функции, описывающие монотонный характер тенденции развития; II) кривые с пределом роста в исследуемом периоде (кривые насыщения); III) S-образные кривые, описывающие два последовательных лавинообразных процесса (рис. 9.13).

Из функций первой группы выделим класс полиномов:

=a₀+a₁t+...+a_pt^p+u_t, (9.27)

где a_i (i=0,…,p) − параметры полинома, t – здесь и далее − время.

Полином первой степени отражает равномерное во времени возрастание или убывание значений ряда. Полином второй степени может выражать тенденцию возрастания и последующего убывания значений ряда или наоборот и т.д. Обычно p мало по сравнению с n. При этом a₁ представляет оценку скорости роста, a₂ − ускорения роста, a₃ − изменения ускорения. Обычно в экономических исследованиях порядок полинома p не превышает трех. Вопрос о степени полинома решается для каждой задачи отдельно на основе проверки гипотез о равенстве нулю коэффициентов при старших степенях в формуле (9.27) до тех пор, пока гипотеза о равенстве нулю коэффициента a_p отклоняется.

Для получения оценок коэффициентов в формуле (9.27) используется метод наименьших квадратов (МНК). Обозначим − расчетное значение. Тогда

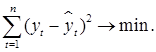
В результате минимизации указанного выражения получаем систему нормальных уравнений:

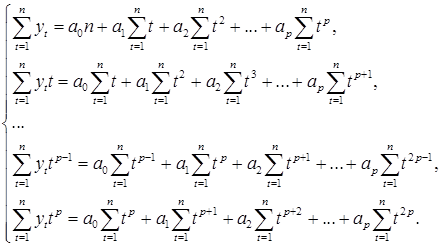(9.28)

Система состоит из (p+1) линейных уравнений. Решение системы дает оценки искомых коэффициентов.

В частности, для нахождения параметров линейного тренда =a₀+a₁t система (9.28) упрощается и имеет вид

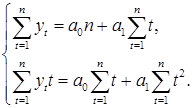
Решение системы дает оценки параметров линейного тренда:

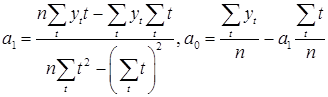Для параболического тренда p=2 и =a₀+a₁t+a₂t² получаем

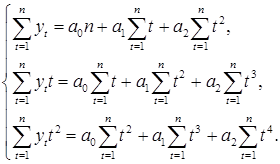
Решение системы дает оценки параметров параболы.

Составление и решение системы нормальных уравнений можно упростить путем переноса начала координат в середину ряда динамики. Это приводит к тому, что суммы по времени при k − нечетном. Если до переноса начала координат t было равно 1, 2, 3, …, то после переноса для четного числа членов ряда: t = …, -5, -3, -1, 1, 3, 5, …, для нечетного числа членов ряда: t = …, -3, -2, -1, 0, 1, 2, 3, …

Тогда оценки параметров для прямой вычисляются по формулам:

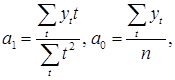
для параболы по формулам:

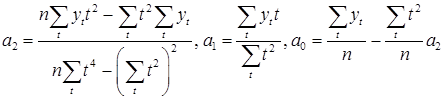Для класса показательных (экспоненциальных) кривых роста характерна зависимость приростов от значений самой функции (рис. 9.13).

Простая экспонента имеет вид

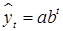причем при b>1 кривая возрастающая функция по t, а при b<1 − убывающая.

Очевидным преобразованием экспонента приводится к виду

введением новой переменной . Для идентификации параметров линеаризованной функции применяется МНК.

a₁>0 a₂>0

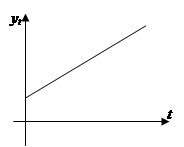
полином первого полином второго полином третьего

порядка =a₀+a₁t порядка =a₀+a₁t+a₂t² порядка =a₀+a₁t+a₂t²+a₃t³

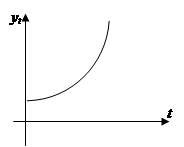b>1 a>0, b<1

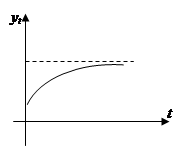
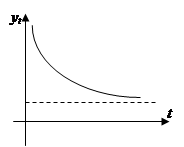
показательная модифицированная гипербола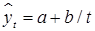

кривая 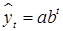экспонента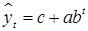

b с

lnc<0, a<1

кривая Гомперца логистическая кривая

Рис. 9.9. Кривые роста

Другой популярной кривой роста является степенная функция: , значения неизвестных параметров a и b которой могут быть получены МНК после применения к функции линеаризующего преобразования, приводящего к виду .

Из функций второго класса (имеющих пределы насыщения − асимптоты) отметим гиперболическую функцию:

1-го типа , 2-го типа , 3-го типа .

Соответственно возможна замена переменных: в первом случае; во втором случае; в третьем случае.

Также асимптоту имеет модифицированная экспонента 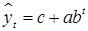(рис. 9.13).

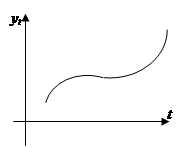
Из кривых третьего класса, имеющих точку перегиба и относящихся к S-образному типу отметим логистическую кривую (кривая Перла-Рида):

Логистическая функция возрастает сначала ускоренным темпом, затем темп роста замедляется и наконец рост почти полностью прекращается и кривая приближается к асимптоте параллельной оси абсцисс. С помощью этой функции хорошо описывается развитие новой отрасли, динамика инновационных проектов и т.п.

Также к S-образному типу относится кривая Гомперца

Кривая несимметрична. После логарифмирования получим:

Наибольший интерес для экономических задач представляет вариант этой кривой, когда lnc<0 и a<1.

Выбор кривой осуществляется либо визуально, либо с использованием метода последовательных разностей (для полиномов). При идентификации параметров МНК можно подобрать форму кривой по, например, минимальному значению среднеквадратической ошибки.