Анализ и управление производственными запасами.
Производственные запасы в широком смысле слова понимаются как сырье и материалы, необходимые для производственного процесса, включая малоценные и быстроизнашивающиеся предметы, а также незавершенное производство, готовая продукция на складе, и сопутствующие товары для перепродажи.
Очевидно, что для деятельности любой организации необходимы какие-то запасы. Если их не будет, то при малейшем нарушении сбыта вся деятельность остановится. Хранить же слишком много производственных запасов экономически невыгодно. Поэтому задача управления производственными запасами посвящена нахождению компромисса между этими двумя крайностями.
Стратегия управления производственными запасами предполагает ответ на два вопроса:
- какова должна быть структура производственных запасов?
- каков должен быть объем производственных запасов?
1.1. Модель Уилсона (базовая)
Если вопрос о составе и структуре производственных запасов обычно не основывается на каких - либо формализованных моделях, то при ответе на вопрос об объеме запасов существуют наработанные подходы. В этой связи цель предприятия – разработка такой программы, при которой общая сумма затрат на производство и содержание запасов минимизируется при условии полного и своевременного удовлетворения спроса на продукцию.
Алгоритмизация политики управления величиной запасов требует ответа на следующие вопросы:
- можно ли в принципе оптимизировать величину производственных запасов?
- какой объем запасов является минимально необходимым?
- когда следует заказывать очередную партию запасов?
- каков должен быть оптимальных объем заказываемой партии?
Решение подобных оптимизационных задач предполагает идентификацию целевого критерия оптимизации. В отношении запасов таким критерием принято считать затраты на поддержание производственных запасов, которые (затраты) укрупненно принято делить на:
- затраты по хранению запасов;
- затраты по выполнению заказов;
Цель модели оптимального размера заказа состоит в обосновании и выборе такого размера заказа Q (в натуральных единицах), который обеспечивает минимальные совокупные годовые затраты по поддержанию необходимого уровня товарно-материальных запасов. При этом обычно предполагается, что компания расходует запасы с некоторой постоянной скоростью и возобновляет заказы по мере исчерпания запасов до нуля (рис.1)
Описанная модель, известная как модель Уилсона, позволяет определить потребности в финансировании поставок товарно-материальных ценностей, т.е. запасов, при планируемом увеличении объемов продаж.
1.2. Модель, учитывающая скидки
Как уже отмечалось, излишнее увеличение материальных запасов предприятиям экономически невыгодно. При этом базовая модель Уилсона предполагает независимость цены приобретения (С) товара от объема закупки. Однако реальным хозяйствующим субъектам поставщики могут предоставлять скидки в зависимости от размера приобретаемой партии. В этом случае перед финансовыми менеджерами предприятия стоит вопрос о выяснении такого размера скидок, которые за отчетный период компенсируют повышенные расходы на хранение приобретаемой продукции.
В этом случае в общую модель суммарных издержек (1) необходимо добавить фактически понесенные затраты Спр на приобретение товара:
CΣ = Cc + Co + Спр = I*Q/2 + F*D/Q + С*D, (5)
1.3. Модель планирования экономического размера партии
Основную модель, используемую для моделирования процессов приобретения запасов у внешнего поставщика можно распространить и на другие производственные ситуации, большинство из которых предполагает частичное восполнение запасов за счет их производства на данном предприятии.
В этом случае исходное допущение модели Уилсона о мгновенном изменении уровня запасов от 0 до Q не может быть принято. Это изменение в действительности характеризуется некоторым временным интервалом t в течение которого происходит увеличение запасов (рис.2). В этом случае принято говорить о модели с продолженной поставкой, и в качестве параметра оптимизации здесь выступает оптимальный размер партии запасов, произведенной своими силами. За это же время (t) происходит одновременное потребление произведенного ресурса.
Очевидно, что в этом случае восполнение запасов происходит в количестве H (H < Q), причем средний уровень запасов на предприятии равен H/2. Если обозначить через λ интенсивность производства (шт./ед.вр.) и через γ – интенсивность потребления (шт./ед.вр. ), то
H = t*(λ - γ), где t=Q/λ,
откуда средний запас равен 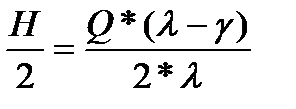 , (6)
, (6)
и при известном числе партий (т.е. тех же самых заказов на поставку, только не от сторонних поставщиков) n = γ/Q
суммарные затраты производства СΣ можно представить в виде:
СΣ = I*H/2 + F*n  + F*γ /Q , (7)
+ F*γ /Q , (7)
откуда
| Q |
| Qk |
| выручка |
| TC |
| FC |
| руб |
| break-even-point |
Q* =
 (8)
(8)
1.4. Оптимизация производственных запасов
с учетом страхового запаса
Предыдущие рассуждения основывались на допущении, что возобновление производственных запасов происходит лишь при их исчерпании до нуля. Разумеется, в реальной экономической жизни предприятия чаще всего не допускают подобной ситуации. В этой связи существует понятие точки перезаказа (уровня возобновления заказа), которую в условиях определенности и ритмичности функционирования хозяйствующего субъекта определяют как произведение количества дней, необходимых для исполнения заказа поставщиком, на среднедневную интенсивность потребления данного товара.
Формирование оптимального заказа и определение точки перезаказа позволяют сократить издержки по двум группам затрат - на размещение заказа и на хранение приобретенных запасов. Однако потребность в материалах и сроки поставки во многом зависят от поведения покупателей (колебания спроса) и поставщиков (нарушение сроков поставки). Неопределенность потребностей и нарушение сроков поставок приводят к тому, что возникает вероятность дефицита запасов и, как следствие, убытков от простоя, потеря платежеспособного спроса и т.д. При этом увеличение размера заказа не снижает вероятности возникновения дефицита, поскольку дополнительные материалы поступят уже после того, как возникнет дефицит.
В этой связи принято говорить о страховом запасе. Создание страхового запаса – это увеличение объема запасов, принимаемого за точку презаказа. Это – расчетная величина, которая влияет на точку перезаказа.
Для расчета оптимального размера страхового запаса в условиях неопределенности используются методы математической статистики и теории вероятностей. При этом можно рекомендовать следующую формулу расчета страхового запаса:
Страховой запас = k*  (9)
(9)
где k — коэффициент безопасности, который определяет степень защиты от дефицита, рассчитывается в зависимости от принятого значения вероятности дефицита;
LT - средняя длительность выполнения заказа;
d - среднее значение потребности в сырье и материалах;
var d, var LT - среднеквадратические отклонения потребности соответст венно в сырье и материалах и времени выполнения заказа.
Объем страхового запаса во многом зависит от принятия или непринятия риска менеджментом компании. Но, как правило, финансовые директора не могут ответить на вопрос, какая вероятность возникновения убытков приемлема для их предприятия. Разумеется, гораздо безопаснее исключить такую вероятность вообще, но это приведет к созданию значительных страховых запасов, которыми предприятие ни разу не воспользуется.
Оптимальная вероятность убытков вследствие дефицита запасов (Р), то есть вероятность, при которой сумма убытков от простоя и затрат на хранение страхового запаса минимальна, может быть рассчитана по формуле:
P =  (10)
(10)
где C — затраты на хранение одной единицы запасов за рассматриваемый период;
U — убытки из-за дефицита одной единицы запаса;
N — количество заказов за рассматриваемый период.
Нужно отметить, что данный метод применим при большом количестве операций, когда работают законы статистики. Практика показывает, что предположение о нормальном распределении случайных величин (потребности в запасах, времени выполнения заказа) дает наилучшие результаты при моделировании управления запасами.