Резонанс напряжения в цепи переменного тока.

рассмотренная цепь из последовательно соединенных индуктивности, емкости и активного сопротивления может рассматриваться как колебательная система, так как в ней возможно возникновение электромагнитных колебаний с собственной частотой

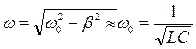при .

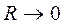Эти колебания являются затухающими, так как энергия, сосредоточенная в контуре в момент возникновения колебаний выделяется в виде тепла на активном сопротивлении во время колебательного процесса.

Тогда, при включении в контур источника переменной ЭДС, его можно рассматривать как элемент, инициирующий в контуре вынужденные колебания с частотой 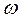. Следовательно, уравнение

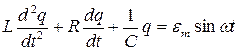представляет собой уравнение вынужденных электромагнитных колебаний под действием внешней периодически изменяющейся ЭДС.

Используя физические величины: собственную частоту 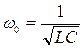и коэффициент затухания 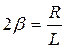это уравнение можно представить и в виде .

Как известно, для вынужденных колебаний характерно явление резонанса, которое заключается в возрастании амплитуды вынужденных колебаний при приближении частоты внешнего воздействия к резонансной частоте, зависящей от параметров колебательной системы.

В рассматриваемой цепи - колебательном контуре вынужденные колебания совершают сила тока, заряд и напряжение на конденсаторе, а также напряжение на катушке индуктивности.

Резонансными кривыми называются зависимости амплитудных значений, совершающих вынужденные колебания физических величин, от частоты внешнего воздействия, т.е., в нашем случае, от частоты источника ЭДС.

Закон Ома для рассматриваемой цепи – колебательного контура позволяет проанализировать зависимость амплитуды силы тока от частоты источника ЭДС: .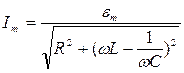

Если амплитудное значение ЭДС, а также величины активного сопротивления, емкости и индуктивности постоянны, то амплитудное значение силы тока зависит только от частоты.

Максимальная амплитуда силы тока: 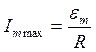при 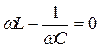. В этом случае частота источника ЭДС совпадает с собственной частотой колебательного контура: ,

т.е. для вынужденных колебаний силы тока наблюдается резонанс.

Резонансная частота для заряда и напряжения всегда меньше, чем резонансная частота для тока, а резонанс выражен тем больше, чем меньше активное сопротивление контура.

 

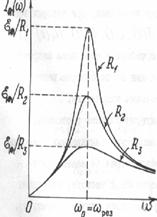
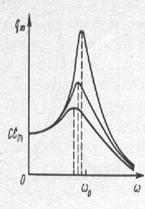
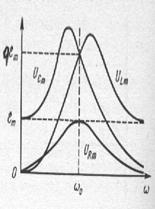
РИС.155 РИС.156 РИС.157 РИС.158

 

Максимальное значение напряжения на катушке индуктивности (см.§ 51) преобразуем также, используя понятия собственной частоты и коэффициента затухания:

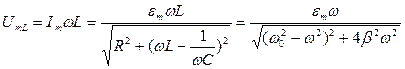. Резонансную частоту можно найти, взяв производную по частоте от этого выражения и приравняв ее к нулю. Резонансная частота для напряжения на катушке индуктивности равна: .

Если преобразовать и сравнить выражения для резонансных частот на конденсаторе и на катушке индуктивности с резонансной частотой тока: 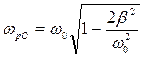, , , то можно сделать вывод, что , общем случае, резонансная частота для напряжения на конденсаторе всегда меньше, а для напряжения на катушке индуктивности всегда больше, чем резонансная частота для силы тока (и напряжения на активном сопротивлении). Резонансные кривые для напряжений на активном сопротивлении, катушке индуктивности и емкости показаны на рис.158.

Для представляющих практический интерес контуров с малым затуханием, 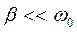, членом можно пренебречь. В этом случае резонанс для всех переменных электрических величин: силы тока, заряда и напряжения на конденсаторе, напряжения на катушке индуктивности наступает практически одновременно при частоте источника, равной частоте свободных колебаний в контуре:

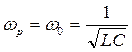. При резонансе сдвиг фаз между током и напряжением равен нулю (рис.159).

Следовательно, добротность – величина обратная относительной ширине пропускания или относительной ширине резонансной кривой.

Резонанс используется для выделения из сложного «сигнала» (зарегистрированного напряжения) нужной составляющей. Это имеет практическое значение в радиотехнике при приеме и настойке на определенную частоту радиосигнала. Чем выше добротность контура, тем уже резонансная кривая и тем легче «отстраиваться» от передач, ведущихся на соседних частотах.

На практике добротность контура подбирается и с учетов необходимого качества приема сигнала, так как с уменьшение ширины резонансной кривой уменьшается информация (диапазон частот) «пропускаемый» контуром.

Электрическое поле при наличии постоянного тока. Уравнение непрерывности. Обобщенный закон Ома. Сторонние электродвижущие силы.