СИЛЛАБУС
Кафедрасы
Оқу пәні: AG1205 Алгебра және геометрия (2 кредит )
Мамандық:5В060400 Физика
Курс:1
Оқытушы:Ниязмағамбетов К.Н.
2014 -2015 оқу жылы
Пән AG 1205 Алгебра және геометрия ( 2 кредит )
| Сабақ өткізу уақыты мен орыны | ОСӨЖ-ның өткізу уақыты мен орыны | Оқытушының аты-жөні | Байланыс, тел, email |
| сабақ кестесіне сәйкес | Кесте бойынша | Ниязмағамбетов К.Н. |
ОҚУ ПӘНІНІҢ МАҚСАТ-МІНДЕТТЕРІ,СИПАТЫ:сызықты тәуелсіздік, ранг,сызықты кеңістік,сызықты және бисызықты түрлендірулер ұғымдарында көрініс табатын бөлігі негізгі алгебралық ұғымдарға сай геометриялық интуиция мен танымды қалыптастыруға арналған. Ал алгебралық аппарат геометриялық құрылымдар мен түрлендірулерде кездесетін нысандар мен есептерді компьютерде практикалық есептеу және компьютерлік графика деңгейіне жеткізуге арналған.
ОҚУ ПӘНІНІҢ ҚЫСҚАША МАЗМҰНЫ: сызықты алгебралық теңдеулер жүйесінің теориясын, бірінші және екінші ретті алгебралық қисықтар,беттер мен гипербеттердің негізгі түрлерін,матрицалар мен анықтауыштар теориясын,Гаусс теоремасы және оның салдарын,сызықты кеңістік,базисі және вектор координаталары ұғымдарын, квадраттық формалар теориясын меңгереді.
КУРС ПРЕРЕКВИЗИТІ:Мектептің математика курсы.
КУРС ПОСТРЕКВИЗИТІ: Математикалық анализ,физиканың жалпы курсы.
БІЛІМДІ БАҒАЛАУ:
Ағымдағы бағалау: осы курстың барысында бағалау стратегиясы ретінде бағалаудың келесі әдістері пайдаланылады: жазбаша бақылау жұмыстары, үй тапсырмалары (математикалық көрсеткіштері, анализдері, алынған салыстырмалы мәліметтер бар, жазбаша тапсырмалар және т.с.с.), ауызша сұрау, тесттік тапсырмалар, зерттеу жұмыстары (жоба, курстық, презентациялар), мәнжазба, эссе және т.с.с.
Аралық бақылау (бақылау жұмысы):бақылау жұмысы курста өткен бөлімдер бойынша теориялық және практикалық, лабораториялық (есептеу, графикалық-есеп және шығармашылық) тапсырмаларды қамтиды.
Жеке өзіндік жұмыс:курс тақырыптары бойынша семинар сабақтарында тапсырмалар, үй тапсырмаларын, шығармашылық тапсырмаларды, мәнжазбаларды жеке орындау, ситуацияларды талдау, ғылыми деректерді, газеттік ақпаратты пайдалану ескеріледі.
Үй тапсырмасы:үй тапсырмаларын студенттер міндетті түрде дайындайды және ОСӨЖ (ОМӨЖ) сабақтарында барлық топтар кесте бойынша тапсырады. Белгіленген уақыт мерзімінен кейін тапсырылған үй тапсырмаларына баға төмендетіледі.
Коллоквиум:өткен материал бойынша студенттен семестрде екі рет ауызша немесе жазбаша жауап алу түрінде жүргізіледі.
Курстық жұмыс, мәнжазба, эссе, презентация,графикалық-есеп жұмысы:нақты тақырып бойынша тапсырылады, кішігірім шығармашылық жұмыс болып табылады. Бағалау кезінде тақырыптың мазмұнының ашылуы, ғылыми деректердің пайдаланылуы, баяндалу стилі, көрнекіліктің пайдаланылуы ескеріледі. Жұмыстар бекітілген мерзімнен кейін қабылданбайды және бағаланбайды.
Аралық бақылау тесттері:өткен материалдар бойынша 10 және одан жоғары тапсырмаларды қамтитын тесттер. Тестілеу семестрде екі рет 7 және 15 апталарда кесте бойынша өткізіледі.
Қорытынды емтихан:қорытынды емтихан семестр соңында өткізіледі. Емтихан қабылданатын күн деканаттың емтихан кестесінде көрсетіледі. Емтихан компьютерлік тестілеу нысанында жүргізіледі. Тесттер курс бағдарламасының барлық бөлімдері бойынша тапсырмаларды қамтиды. Емтихан кезінде дәріс конспектілерін, кітаптарды, әртүрлі жазбаларды пайдалануға тыйым салынады. Төмен баға алған жағдайда, оны көтеру үшін, қосымша басқа тапсырмалар берілмейді. Емтиханды өткізу саясатын сақтамаған студент, емтиханды тапсырудан босатылып, емтиханды тапсырмаған болып есептелінеді.
Қорытынды баға: студенттер семестр соңында пәндер бойынша 100 (40%) балмен бағаланатын емтихан тапсырады.
МОДУЛЬ БОЙЫНША ПӘННІҢ ТАҚЫРЫПТЫҚ ЖОСПАРЫ:
| № | Модульдің атауы | Лекция (сағ) | Практикалық (семинар.) сабақ (сағ) | СӨЖ (сағ) | |
| Матрицалар және анықтауыштар | |||||
| Сызықтық вектор кеңістіктігі | |||||
| Жазықтықтағы және кеңістіктегі І ретті сызықтық арифметикалық бейнелер. ІІ ретті қисықтар мен беттер | |||||
| Барлығы | |||||
ЛЕКЦИЯ ТАҚЫРЫПТАРЫ:
| Апта | Дәріс жоспары, негізгі дидактикалық бірліктер | Сағаты |
| Модуль 1 | ||
| 1-2 | Матрицалар және анықтауыштар | |
| 3-4 | Сызықты теңдеу жүйесі | |
| Негізгі алгебралық структуралар (топ, сақина,өріс). Мысалдар | ||
| Модуль 2 | ||
| Сызықтық вектор кеңістіктігі.Сызықтық түрлендірулер.Меншікті векторлар және меншікті мәндер. | ||
| Евклид кеңістігі.Коши-Буняковский теңсіздігі. | ||
| Модуль 3 | ||
| 8,9,10 | Жазықтықтағы және кеңістіктегі І ретті сызықтық арифметикалық бейнелер | |
| 11,12,13 | ІІ ретті қисықтар мен беттер | |
| 14,15 | Квадратттық формулалар | |
| Барлығы |
Практикалық (семинарлық) сабақ тақырыптары
| Апта | Практика жоспары, негізгі дидактикалық бірліктер | Сағаты |
| Модуль 1 | ||
| 1-2 | Матрицалар және анықтауыштар | |
| 3-4 | Сызықты теңдеу жүйесі | |
| Негізгі алгебралық структуралар (топ, сақина,өріс). Мысалдар | ||
| Модуль 2 | ||
| Сызықтық вектор кеңістіктігі. Сызықтық түрлендірулер.Меншікті векторлар және меншікті мәндер. | ||
| Евклид кеңістігі. Коши-Буняковский теңсіздігі. | ||
| Модуль 3 | ||
| 8,9,10 | Жазықтықтағы және кеңістіктегі І ретті сызықтық арифметикалық бейнелер | |
| 11,12,13 | ІІ ретті қисықтар мен беттер | |
| 14,15 | Квадратттық формулалар | |
| Барлығы |
1. 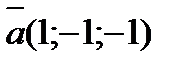 векторының ұзындығын табу?
векторының ұзындығын табу?
А) 3В)1 С) -1 Д) Е) 0,5
Е) 0,5
2.  ,
, 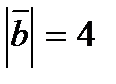 ,
, 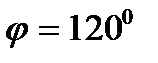 берілген. Векторлардың
берілген. Векторлардың 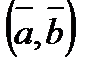 скаляр көбейтіндісін табу?
скаляр көбейтіндісін табу?
А) -5 В) 0 С) -4 Д) 5 Е) 1
3. 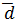 (1;2;1)векторын
(1;2;1)векторын 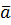 (1;0;1),
(1;0;1),  (0;1;2),
(0;1;2), 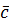 (0;1;1)векторлары арқылы жіктеп жазу керек.
(0;1;1)векторлары арқылы жіктеп жазу керек.
А) 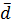 =
= 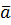 -3
-3  В)
В) 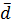 =-
=- 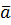 +
+  -
- 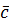 С)
С) 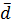 =
=  +4
+4 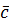 Д)
Д) 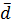 =
=  -4
-4 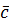 Е)
Е) 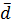 =
= 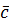
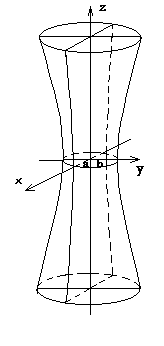
4. Бір қуысты гиперболоидтыңканондық теңдеуі мен суретін көрсет.
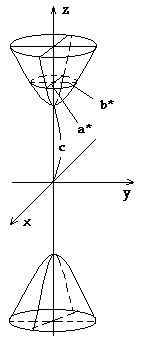
 1)
1)
2) 3)
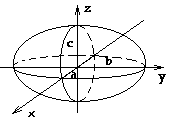 4)
4) 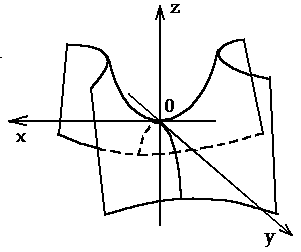 5)
5)
6) 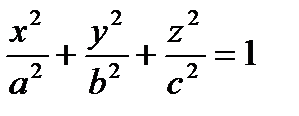 7)
7)  8)
8)  9)
9) 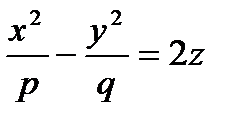 10)
10) 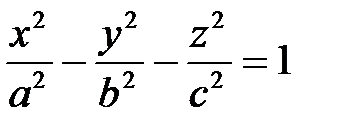
A) 4 және 6 B) 1 және5C) 1 және 8 D) 4 және 10 E)3 және 7
5. 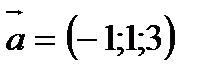 және
және  векторлары перпендикуляр болуы үшін
векторлары перпендикуляр болуы үшін 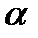 -ның мәні қандай болуы керек? А)
-ның мәні қандай болуы керек? А) В)
В)  С)
С) 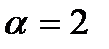 Д)
Д) 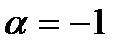 Е)
Е) 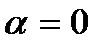
6.  (-1, 2, 0),
(-1, 2, 0), 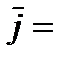 (0, 1, 0) векторлары берілген. Cos (
(0, 1, 0) векторлары берілген. Cos (  ^
^  ) табу керек.
) табу керек.
A) 2 B) 2/  C)
C) 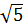 D) 5 E) 10
D) 5 E) 10
7. 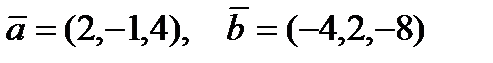 векторлары берілген. Векторлық көбейтіндіні тап (axb)
векторлары берілген. Векторлық көбейтіндіні тап (axb)
А) {-12; 8; 12} В){-2; 0; 5} С) {0;0;0} Д){1;1;1} Е) {0;0;-12}
8. 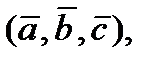 векторларының аралас көбейтіндісін тап,егер
векторларының аралас көбейтіндісін тап,егер 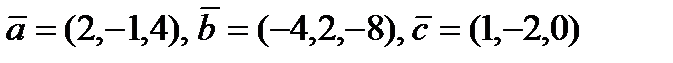
A) 5 B) 4 C) 0D) 6 E)1
9. Түзудің жалпы теңдеуін табу:
А) 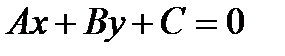 В)
В)  С)
С) 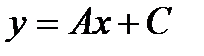 Д)
Д)  Е)
Е) 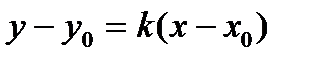
10. 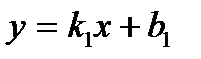 ,
, 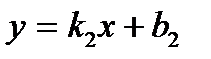 түзулері берілген. Түзулердің перпендикулярлық және параллельдік шарттарын көрсету. А)
түзулері берілген. Түзулердің перпендикулярлық және параллельдік шарттарын көрсету. А) 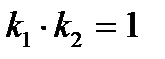 ;
;  В)
В)  ;
;  С)
С) 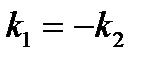 ;
; 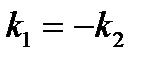
Д)  ;
;  Е)
Е)  ;
; 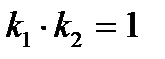
11. 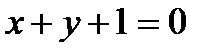 және
және  түзулердің арасындағы бұрышты табу.
түзулердің арасындағы бұрышты табу.
А) 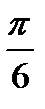 В)
В) 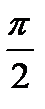 С)
С)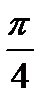 Д)
Д)  Е)
Е) 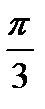
12. А(-2;-1) нүктесінен 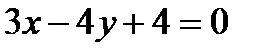 түзуіне дейінгі қашықтық қаншаға тең?
түзуіне дейінгі қашықтық қаншаға тең?
А)0,2 В) 0,4 С)2,5 Д)2 Е) 1
13. А(5;-3) нүктесі арқылы өтетін жәнеx+2y+3=0 түзуіне параллель түзудің теңдеуін құрыңз.
А) 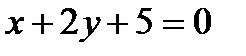 В)
В) 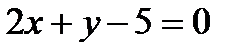 С)x+2y-3=0 Д) x-2y-1=0 Е) x+2y+1=0
С)x+2y-3=0 Д) x-2y-1=0 Е) x+2y+1=0
14. Түзудің теңдеуі берілген  . А(3;1), В(1;5), С(1;3) және Д(8;2) нүктелерінің қайсысы осы түзуде жатады: А)А және Д В) В және С С) А және В Д)С және Д Е)В және Д
. А(3;1), В(1;5), С(1;3) және Д(8;2) нүктелерінің қайсысы осы түзуде жатады: А)А және Д В) В және С С) А және В Д)С және Д Е)В және Д
15. А(3;-1) нүктесінен өтетін және 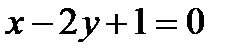 түзуіне параллель болатын түзудің теңдеуін құрыңыз. А)
түзуіне параллель болатын түзудің теңдеуін құрыңыз. А) 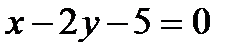 В)
В) 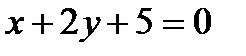 С)
С) 
Д) 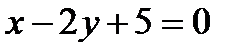 Е)
Е) 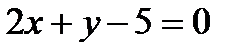 16. А(3;-1) нүктесінен өтетін және берілген
16. А(3;-1) нүктесінен өтетін және берілген 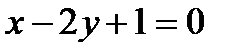 түзуіне перпендикуляр болатын түзудің теңдеуін құрыңыз. А)
түзуіне перпендикуляр болатын түзудің теңдеуін құрыңыз. А) 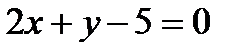 В)
В)  С)
С) 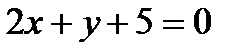 Д)
Д) 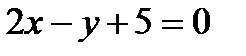 Е)
Е) 
17. С-тің қандай мәнінде  және
және 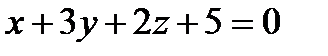 жазықтықтары перпендикуляр болады? А)-7 В)–6 С)6 Д)3 Е)1
жазықтықтары перпендикуляр болады? А)-7 В)–6 С)6 Д)3 Е)1
18. 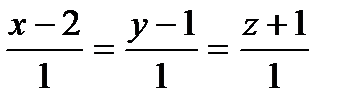 түзуі мен
түзуі мен 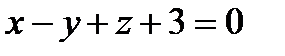 жазықтықтың қиылысу нүктесін табу.
жазықтықтың қиылысу нүктесін табу.
А)(1;2;4) В) (1;-2;4) С) (-1;-2;-4) Д) (-1;2;4) Е)(1;-2;5)
19. 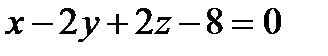 және
және 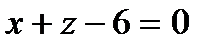 жазықтықтары арасындағы бұрышты табу керек.
жазықтықтары арасындағы бұрышты табу керек.
А)60° В)30° С)120° Д)45° Е)135°
20.А(0;-1;3) және В(1;3;5) нүктелері берілген. А(0;-1;3) нүктесінен өтетін және 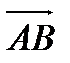 векторына перпендикуляр болатын жазықтықтың теңдеуін жазу керек. А)
векторына перпендикуляр болатын жазықтықтың теңдеуін жазу керек. А) 
В) 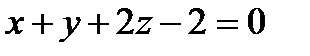 С)
С) 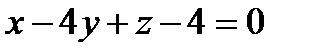 Д)
Д) 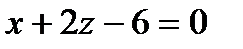 Е)
Е) 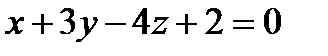
21. А(5;-2;3) және В(1;-3;5) деп алып, 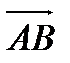 векторына перпендикуляр болатын және координаталар бас нүктесі арқылы өтетін жазықтықтың теңдеуін құру керек А)
векторына перпендикуляр болатын және координаталар бас нүктесі арқылы өтетін жазықтықтың теңдеуін құру керек А) 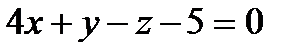 В)
В) 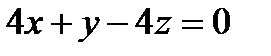 С)
С) 
Д) 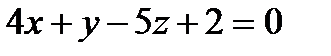 Е)
Е) 
22. Жазықтықтағы 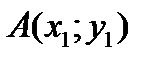 және
және 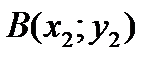 нүктелерінің ара қашықтығын есептеу формуласы:
нүктелерінің ара қашықтығын есептеу формуласы:
А) 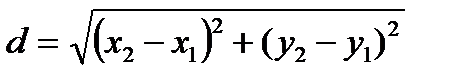 В)
В) 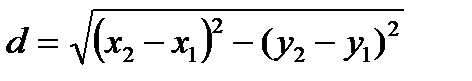 С)
С) 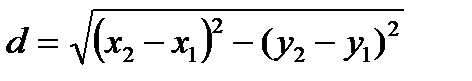
Д) 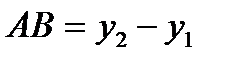 Е)
Е) 
23. 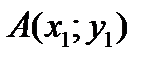 ,
, 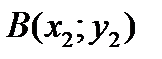 нүктелері берілген. АВ кесіндісін АМ:МВ=
нүктелері берілген. АВ кесіндісін АМ:МВ= 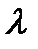 қатынасында қиятын
қатынасында қиятын 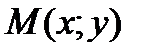 нүктесінің координаттары А)
нүктесінің координаттары А) 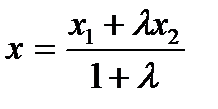 ;
; 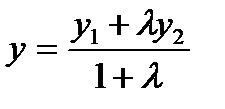 В)
В) 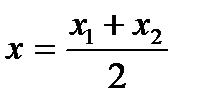 ;
; 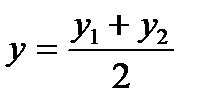
С) 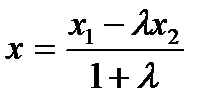 ;
;  Д)
Д) 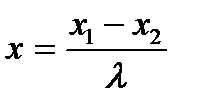 ;
; 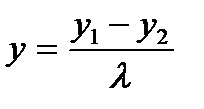 Е)
Е) 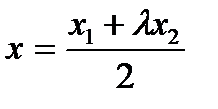 ;
; 
24. 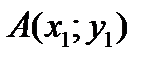 ,
, 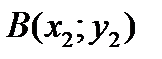 нүктелері берілген. АВ кесіндісінің ортасы болатын
нүктелері берілген. АВ кесіндісінің ортасы болатын 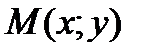 нүктесінің координаталары :
нүктесінің координаталары :
А) 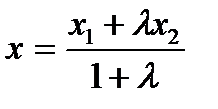
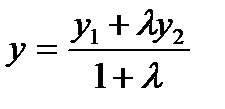 ; В)
; В) 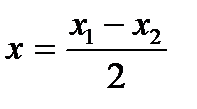
 ;С)
;С) 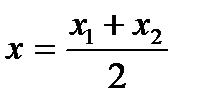 ,
, 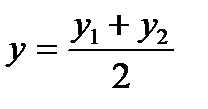 ;
;
Д) 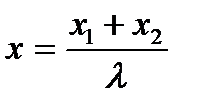 ;
;  Е)
Е) 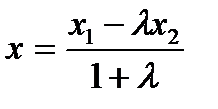 ;
; 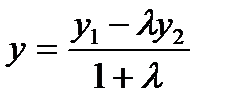
25. 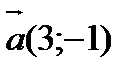 ,
, 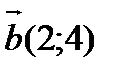 және
және 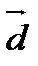 (2,-10) берілген.
(2,-10) берілген. 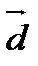 векторын
векторын 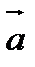 және
және 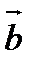 векторлары бағытында жіктеу.
векторлары бағытында жіктеу.
А)  В)
В) 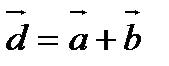 С)
С) 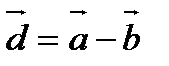 Д)
Д)  Е)
Е) 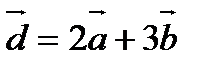

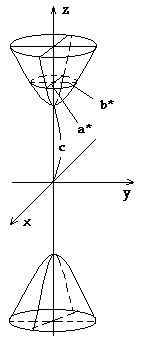 26. Қос қуысты гиперболоидтың канондық теңдеуін көрсету және бейнесін анықтау.
26. Қос қуысты гиперболоидтың канондық теңдеуін көрсету және бейнесін анықтау.
 1) 2) 3) 4)
1) 2) 3) 4) 
 5)
5)
6) 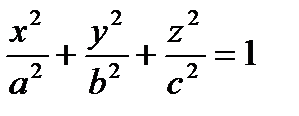 7)
7)  8)
8)  9)
9) 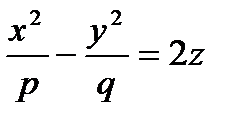 10)
10) 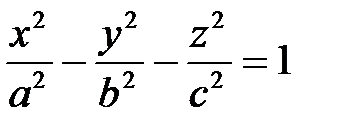
A) 4 и 6 B) 1 и 5C) 1 и 8 D) 2 и 10 E)3 и 7
27. Фокустары координата бас нүктесіне қатысты абсцисса осіне симметриялы жатқан,фокустарының арасы 2с = 12 және эксцентриситеті ε =6 / 7 тең, эллипстің теңдеуін құру?
А) x² ⁄ 36 + y² ⁄ 11 = 1В) x² ⁄ 15 + y² ⁄ 10 = 1 С) x² ⁄ 49 + y² ⁄ 13 = 1
Д) x² ⁄ 11 + y² ⁄ 12 = 1 Е)x² ⁄ 12 + y² ⁄ 49 = 1
28. x² / 49 + y² / 24 = 1 эллипсі берілген. Фокустарын табу.
А) F1(4, 0), F2(-4, 0) В) F1(-3, 0), F2(-3, 0) С) F1(-12, 0), F2(12, 0)
Д) F1(0, -8), F2(0, 8) Е) F1(-5, 0), F2(5, 0)
29. Фокустары абсцисса осінде бас нүктеге қатысты симметриялы орналасқан , осьтері 3а = 15 және 2b = 8 болатын гиперболаның теңдеуін құр?
А)x² ⁄ 5 - y² ⁄ 9 = 1 В) x² ⁄ 49 - y² / 5 = 1 С)x² - 5y² = 25
D) x² ⁄ 7 - y² ⁄ 5 = 1 E) x² ⁄ 9 - y² ⁄ 16 = 1
30.Фокустары координата бас нүктесіне қатысты абсцисса осіне симметриялы жатқан,директрисаларының арасы 12 тең және фокустарының аралығы 2с = 6 тең эллипстің теңдеуін құру. A) x² ⁄ 16 + y² ⁄ 9 = 1 B) x² ⁄ 49 + y² ⁄ 25 = 625 C) x² ⁄ 18 + y² / 9 = 1
D)x² ⁄ 4 + y² ⁄ 3 = 1 E) x² ⁄ 40 + y² ⁄ 20 = 1
31. Эллипстің канондық теңдеуін құру керек, егер эксцентриситеті 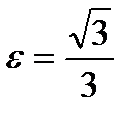 , үлкен жарты осі
, үлкен жарты осі 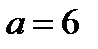 тең болса.
тең болса.
А)x² - 5y² = 25 В) x² ⁄ 9 - y² / 5 = 1 С) x² ⁄ 9 + y² ⁄ 6 = 1 D) x² ⁄ 6 - y² ⁄ 9 = 1 E) x² ⁄ 36 + y² ⁄ 24 = 1
32.z1=6+8i, z2=2-5i комплекс сандарының көбейтіндісін табу?
A) 12+52i B) 26+52i C) 56-56i D) 52-14i E) 12-8i
33. z1 = 5 + 7i және z2 = 4 - 5i комплекс сандары берілген. z1/z2 табу.
A) 12/7+6/7iВ)7/26+25/26iC) -9/41+40/41iD) -25+7iE) -15/41+53/41i
34. Р1: (х-7)/5=(у+11)/2 жәнеР2 : (х+20)/5=(у+3)/2 екі түзу берілген, арасындағы бұрышты тап?
A) 300 B) 450C) 00 D) 600 E) 900
35.a-ның қандай мәнінде векторлары 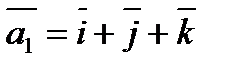 ,
,  ,
, 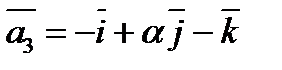 ,
, 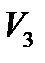 - геометриялық векторлар кеңістігінде базис құра алмайды?
- геометриялық векторлар кеңістігінде базис құра алмайды?
A)  B)
B) 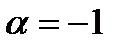 C)
C) 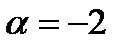 D)
D)  E)
E) 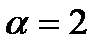 .
.
36.Сызықтық оператордың матрицасы M[ϕ]=  және вектор
және вектор 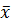 =
= 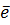 1-4
1-4 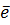 2. берілген. Осы вектордың бейнесі болатын
2. берілген. Осы вектордың бейнесі болатын  - векторын табу керек.
- векторын табу керек.
A)(-25;30)B) (35;25)C) (-35;25)D) (-25;-35)E) (-35;-30)
37. 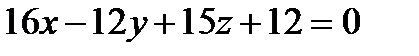 жазықтық пен ОZ осінің қиылысуын табу керек.
жазықтық пен ОZ осінің қиылысуын табу керек.
А) (0;0; -4) В) (1;0;0) С) (0;1;0) Д)  Е)
Е) 
38. АВС үшбұрыштың төбелері берілген А(3;-1:2), В(2;0;1), С(3;1;3). АВС үшбұрышының ауданын табу керек. А) 7 B) 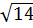 C)
C) 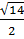 D) 14 E)5/2
D) 14 E)5/2
39. 5х-у+3=0 және -6х+2у+10=0 түзулерінің арасындағы бұрышты есептеу
A)  B)arctg
B)arctg  C)
C) 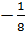 D) - arctg
D) - arctg  E) arctg
E) arctg 
40. Егер А (1;2;-1), B(2;1;3), C(3;2;0) берілсе, 
A)  B)
B)  C)
C)  D)
D)  E)
E) 

А)70В)–70 С) 0 Д)15 Е)20
42. Теңдеуді шешіңіз  = -54
= -54
А) -1 В) 1 С) 0 Д) 2 Е) 3
43.  ,
,  матрицалары берілген. АВ көбейтінді матрицасын табу керек.
матрицалары берілген. АВ көбейтінді матрицасын табу керек.
А)  В)
В)  С)
С)  Д)
Д)  Е)
Е) 
44.  . А2 матрицасын тауып, жауапта элементтерінің қосындысын көрсетіңіз
. А2 матрицасын тауып, жауапта элементтерінің қосындысын көрсетіңіз
А)3 В) 2 С) 1 Д)0 Е)4
45.Қай көбейтіндінің мағынасы жоқ:
A), 
 B)
B) 
 , C)
, C) 
 , D)
, D) 
 E)
E) 

46. Егер  болса,табу керек М-1 -?
болса,табу керек М-1 -?
А)  В)
В)  С)
С)  Д)
Д)  Е)
Е) 
47.Жүйе берілген  .Табу керек
.Табу керек  ?
?
А) -21В)21 С) -15 Д) 15Е)-7
48. 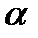 -ның қандай мәнінде
-ның қандай мәнінде  жүйесінің шешімі жоқ.
жүйесінің шешімі жоқ.
А)–1В)1 С) 0 Д)–2 Е)2
49.Сызықты теңдеулер жүйесін шешу үшін Крамер ережесін көрсетіңіз:
А)  В)
В)  С)
С)  Д)
Д)  Е)
Е) 
Бақылау жұмысы 1
Нұсқа 1.
1.Төбелері  нүктелерінде болатын пирамиданың көлемін және
нүктелерінде болатын пирамиданың көлемін және  жағының ауданын есептеу.Суретін салу.
жағының ауданын есептеу.Суретін салу.
А1(1, 0, 3), А2 (1,2,-1), А3 (2,-2,1), А4 (2,1,0).
2.  түзуінің бойында жататын және
түзуінің бойында жататын және  нүктелерінен бірдей қашықтықта орналасқан нүктені табу керек.
нүктелерінен бірдей қашықтықта орналасқан нүктені табу керек.
3.  түзуіне қарағанда
түзуіне қарағанда  нүктесіне симметриялы нүктенің координаталарын табыңдар.
нүктесіне симметриялы нүктенің координаталарын табыңдар.
4.  нүктесінен өтетін, координаталық осьтермен қиылысқанда ауданы 1,5 кв. бірлікке тең және екінші ширекте орналасқан үшбұрыш құратын түзудің теңдеуін жазу керек.
нүктесінен өтетін, координаталық осьтермен қиылысқанда ауданы 1,5 кв. бірлікке тең және екінші ширекте орналасқан үшбұрыш құратын түзудің теңдеуін жазу керек.
5.Квадраттың қарама қарсы төбелері  және
және  берілген. Оның қалған екі төбесінің координаталарын табу және қабырғаларының теңдеулерін жазу.
берілген. Оның қалған екі төбесінің координаталарын табу және қабырғаларының теңдеулерін жазу.
6. .Векторлар aжәнеb өзара перпендикуляр,  . Есепте:
. Есепте:  ;
;  ;
;  .
.
7. Төбелері А(-1,1,-1), В(2,0,4), С(4,3,2) болатын АВС үшбұрышының ауданын тап.
8.  түзуі арқылы өтетін 2x+y-z+7=0 жазықтығына перпендикуляр болатын жазықтықтың теңдеуін жаз.
түзуі арқылы өтетін 2x+y-z+7=0 жазықтығына перпендикуляр болатын жазықтықтың теңдеуін жаз.
9. х-2у+4z-1=0 және 2x-5y+2z+10=0 параллель жазықтықтарының арақашықтығын тап.
10. Екінші ретті қисықтың теңдеуін канондық түрге келтіру және оның түрін анықтау  .
.
Нұсқа 2.
1.Төбелері  нүктелерінде болатын пирамиданың көлемін және
нүктелерінде болатын пирамиданың көлемін және  жағының ауданын есептеу.Суретін салу.
жағының ауданын есептеу.Суретін салу.
А1(2, 0, 2), А2 (1,2,-1), А3 (2,-2,1), А4 (2,1,0).
2.  түзуінің бойында жататын және
түзуінің бойында жататын және  нүктелерінен бірдей қашықтықта орналасқан нүктені табу керек.
нүктелерінен бірдей қашықтықта орналасқан нүктені табу керек.
3.  түзуіне қарағанда
түзуіне қарағанда  нүктесіне симметриялы нүктенің координаталарын табыңдар.
нүктесіне симметриялы нүктенің координаталарын табыңдар.
4.  нүктесінен өтетін, координаталық осьтермен қиылысқанда ауданы 1,5 кв. бірлікке тең және төртінші ширекте орналасқан үшбұрыш құратын түзудің теңдеуін жазу керек.
нүктесінен өтетін, координаталық осьтермен қиылысқанда ауданы 1,5 кв. бірлікке тең және төртінші ширекте орналасқан үшбұрыш құратын түзудің теңдеуін жазу керек.
5.Квадраттың бір қабырғасының теңдеуі  және диагональдарының қиылысу нүктесі
және диагональдарының қиылысу нүктесі  берілген. Квадраттың қалған қабырғаларының теңдеулерін жазу керек.
берілген. Квадраттың қалған қабырғаларының теңдеулерін жазу керек.
6. aжәнеb векторларының арасындағы бұрыш 60 градусқа тең және  . Есепте:
. Есепте:  ;
;  ;
;  .
.
7. Төбелері А(1,-1,1), В(2,3,4), С(4,3,-2) болатын АВС үшбұрышының ауданын тап.
8.  түзуі арқылы өтетін 2x+y-z+4=0 жазықтығына перпендикуляр болатын жазықтықтың теңдеуін жаз.
түзуі арқылы өтетін 2x+y-z+4=0 жазықтығына перпендикуляр болатын жазықтықтың теңдеуін жаз.
9.  и
и  түзулерінің ара қашықтығын тап.
түзулерінің ара қашықтығын тап.
10. Берілген  нүктеден өтетін және эксцентриситеті
нүктеден өтетін және эксцентриситеті  тең гиперболаның теңдеуін жазу керек.
тең гиперболаның теңдеуін жазу керек.
В)-1 С)3 Д) 2 Е)0
СӨЖ тапсырамалары
1. а)  ,
,  ,
,  - векторлары үшбұрыштың қабырғалары. Осы векторлар арқылы
- векторлары үшбұрыштың қабырғалары. Осы векторлар арқылы  ,
,  ,
,  медианаларын өрнектеңіз.
медианаларын өрнектеңіз.
б) Егер  {5,-2,0},
{5,-2,0},  {0,-3,4},
{0,-3,4},  {-6,0,1},
{-6,0,1},  {25,-22,16} векторлары берілген болса, онда
{25,-22,16} векторлары берілген болса, онда  векторын
векторын  ,
,  ,
,  векторлары арқылы өрнектеңіз.
векторлары арқылы өрнектеңіз.
в) |  | = 2 , |
| = 2 , |  | = 1, (
| = 1, (  ) = 600,
) = 600,  және (
және (  +
+  ) векторларының арасындағы бұрыштың косинусын анықтаңыз.
) векторларының арасындағы бұрыштың косинусын анықтаңыз.
г) Егер  {2,3,1},
{2,3,1},  {5,6,4} болса, онда [
{5,6,4} болса, онда [ 
 ] есептеңіз.
] есептеңіз.
д) Егер  {1,-1,2},
{1,-1,2},  {-1,1,1},
{-1,1,1},  {5,6,2} болса, онда
{5,6,2} болса, онда 

 есептеңіз.
есептеңіз.
2. а) АВС үшбұрышында :  ,
,  . ВС қабырғасы 5 бөлікке бөлінген.
. ВС қабырғасы 5 бөлікке бөлінген.  ,
,  ,
,  ,
,  векторларын
векторларын  және
және  векторлары арқылы өрнектеңіз
векторлары арқылы өрнектеңіз
б) Егер  {3,5,6},
{3,5,6},  {2,-7,1},
{2,-7,1},  {12,0,6},
{12,0,6},  {0,20,18} векторлары белгілі болса, онда
{0,20,18} векторлары белгілі болса, онда  векторын
векторын  ,
,  ,
,  векторлары арқылы өрнектеңіз
векторлары арқылы өрнектеңіз
в) Егер  ,
, 
 болса, онда а2+3
болса, онда а2+3 
 – 2
– 2 
 + 1 өрнегін ықшамдаңыз, мұндағы m2 = 4, n2 = 1, (
+ 1 өрнегін ықшамдаңыз, мұндағы m2 = 4, n2 = 1, (  ) =
) = 
г)  {8,4,1},
{8,4,1},  {2,-2,1} векторларында құрылған параллелограмның ауданын табыңыз.
{2,-2,1} векторларында құрылған параллелограмның ауданын табыңыз.
д)  {2,-1,3},
{2,-1,3},  {1,4,2},
{1,4,2},  {3,1,-1} векторлары компланар бола ма?
{3,1,-1} векторлары компланар бола ма?
3. а) Кез келген үшбұрыштың медиана - векторлары басқа үшбұрыштың қабырғалары болатынын көрсетіңіз.
1. б) Егер  {5,2,1},
{5,2,1},  {-1,4,2},
{-1,4,2},  {-1,-1,6},
{-1,-1,6},  {3,5,9} векторлары берілген болса, онда
{3,5,9} векторлары берілген болса, онда  векторын
векторын  ,
,  ,
,  векторлары арқылы өрнектеңіз.
векторлары арқылы өрнектеңіз.
в)  =
=  ,
,  =
=  векторларына салынған параллелограмның диагональдарының ұзындығын есептеңіз, мұндағы
векторларына салынған параллелограмның диагональдарының ұзындығын есептеңіз, мұндағы 
 , (
, (  ) =
) = 
г) Егер  {5,-2,1},
{5,-2,1},  {4,0,6} болса, онда
{4,0,6} болса, онда  х
х  есептеңіз.
есептеңіз.
д)  {3,1,-2},
{3,1,-2},  {-4,0,3},
{-4,0,3},  {1,5,1} векторларына салынған параллелепипедтің көлемін анықтаңыз.
{1,5,1} векторларына салынған параллелепипедтің көлемін анықтаңыз.
4. а) АВС үшбұрышында :  ,
,  ,
,  . Бұрыштардың биссектрисаларына коллинеар векторларды анықтаңыз.
. Бұрыштардың биссектрисаларына коллинеар векторларды анықтаңыз.
б) Егер  {6,4,2},
{6,4,2},  {-9,6,3},
{-9,6,3},  {-3,6,3},
{-3,6,3},  {-9,2,1} берілген болса, онда
{-9,2,1} берілген болса, онда  векторын
векторын  ,
,  ,
,  векторлары арқылы өрнектеңіз.
векторлары арқылы өрнектеңіз.
в)  ,
,  ,
,  векторлары үшбұрыштың қабырғалары, мұндағы
векторлары үшбұрыштың қабырғалары, мұндағы  ^
^  , |
, |  | = |
| = |  | = 1. Үшбұрыштың бұрыштарын табыңыз.
| = 1. Үшбұрыштың бұрыштарын табыңыз.
г)  {2,1,-1},
{2,1,-1},  {-3,0,2} векторларына салынған параллелограмның ауданын табыңыз.
{-3,0,2} векторларына салынған параллелограмның ауданын табыңыз.
д) Егер  {4,7,3},
{4,7,3},  {1,2,1},
{1,2,1},  {2,-3,-1}болса,
{2,-3,-1}болса, 

 аралас көбейтіндісі неге тең?
аралас көбейтіндісі неге тең?
5. а) Дұрыс үшбұрыштың төбелерін оның центрімен қосатын векторлардың қосындысы нөлдік вектор. Дәлелдеңіз.
б) Егер  {6,-18,12},
{6,-18,12},  {-8,24,-16},
{-8,24,-16},  {8,7,3},
{8,7,3},  {0,31,-13} берілген болса, онда
{0,31,-13} берілген болса, онда  векторын
векторын  ,
,  ,
,  векторларымен өрнектеңіз.
векторларымен өрнектеңіз.
в)  векторы берілген, оның ұзындығын тауып, келесі бұрыштарды есептеңіз: (
векторы берілген, оның ұзындығын тауып, келесі бұрыштарды есептеңіз: (  ), (
), (  ), (
), (  )
)
г) Егер  {-2,6,-4},
{-2,6,-4},  {3,-9,6}
{3,-9,6}  х
х  векторлық көбейтіндісін есептеңіз.
векторлық көбейтіндісін есептеңіз.
д)  {1, 6, 5},
{1, 6, 5},  {3, -2, 4},
{3, -2, 4},  {7, -18, 2}.компланар бола ма?
{7, -18, 2}.компланар бола ма?
6. а): x + y – 3 = 0, 2x + 3y – 8 = 0 түзулерінің қиылысу нүктесін тауып, арасындағы бұрышты есептеңіз.
б) А(1,-2), В(0,3), С(1,1) нүктелері АВС үшбұрышының төбелері. Үшбұрыштың төбелерінен өтетін және қарсы қабырғаларына параллель түзудің теңдеуін жазыңыз.
в) (-3,1),(5,7) ромбының қарсы жатқан төбелері және ромбтың ауданы S=25. Ромбтың қабырғаларының теңдеуін жазыңыз.
7. а) x – 2y + 3 = 0, 2x + y – 5 = 0 түзулерінің қиылысу нүктесін тауып, арасындағы бұрышты есептеңіз.
б) А(1,-2), В(3,2) нүктелері ABCD параллелограмының іргелес төбелері және оның диагональдарының қиылысу нүктесі Р(1,1). Параллелограмның қабырғаларының теңдеуін жазыңыз.
в) x + y – 8 = 0 түзуінен (2,8) нүктесінен және x – 3y + 2 = 0 түзуінен бірдей қашықтықта орналасқан нүктені тап.
8. а) x – y + 5 = 0, 2x – 2y + 3 = 0 түзулерінің қиылысу нүктесін тауып, арасындағы бұрышты есептеңіз.
б) Параллелограмның іргелес қабырғалары келесі теңдеулермен берілген: x – y – 1 = 0 және x – 2y = 0. F(3,-1) оның диагональдарының қиылысу нүктесі. Параллелограмның қабырғаларының теңдеуін жазыңыз.
в) 4x – 3y + 1 = 0, 3x – 8y + 41 = 0, x + 5y – 17 = 0 үшбұрыштың қабырғаларының теңдеуі. Үшбұрыштың ауданын табыңыз.
9. а) 2x – 3y + 6 = 0, 2x – 3y + 4 = 0 түзулерінің қиылысу нүктесін тауып, олардың арасындағы бұрышты есептеңіз.
б) M(2,-1), N(-3,-3), P(-1,0) үшбұрыштың қабырғаларының ортасы. Үшбұрыштың қабырғаларының теңдеуін жазыңыз.
в) 2x – y – 10 = 0 түзуінен М(-5,0), N(-3,4) нүктелеріне дейінгі қашықтықтың қосындысы ең аз болатындай нүктені табыңыз.
10. а) x – 2y + 4 = 0, –2x + 4y – 8 = 0 түзулерінің қиылысу нүктесін тауып, олардың арасындағы бұрышты есептеңіз.
б) А(-1,5), В(3,2) нүктелері rАВС үшбұрышының төбелері, ал Н(5,3) үшбұрыштың биіктіктерінің қиылысу нүктесі. Оның қабырғаларының теңдеуін жазыңыз.
в) Қабырғалары 2x + 3y – 13 = 0, x + 2y – 7 = 0, x + y – 5 = 0 теңдеулерімен берілген үшбұрыштың ауданын есептеңіз
11. а)А(1,2) нүктесінен өтіп координаттар өстерін жанайтын шеңбердің теңдеуін жазыңыз.
б)  эллипссінен кіші өстен 5 см қашықтықта орналасқан нүктенің координаттарын есептеңіз.
эллипссінен кіші өстен 5 см қашықтықта орналасқан нүктенің координаттарын есептеңіз.
в)  гиперболаның аситоталары және М(12,3
гиперболаның аситоталары және М(12,3  ) гиперболаға тиісті нүкте. Гиперболаның теңдеуін жазыңыз.
) гиперболаға тиісті нүкте. Гиперболаның теңдеуін жазыңыз.
г)  параболаның теңдеуі. М(3,1) нүктесі ортасы болатындай оның хордасының теңдеуін жазыңыз.
параболаның теңдеуі. М(3,1) нүктесі ортасы болатындай оның хордасының теңдеуін жазыңыз.
12. а)  түзуі мен
түзуі мен  шеңберінің қиылысу нүктелерінен және А(4,4) нүктесінен өтетін шеңбердің теңдеуін жазыңыз.
шеңберінің қиылысу нүктелерінен және А(4,4) нүктесінен өтетін шеңбердің теңдеуін жазыңыз.
б)М(  , –2) және N(
, –2) және N(  ,1) нүктелерінен өтетін эллипстің теңдеуін жазыңыз.
,1) нүктелерінен өтетін эллипстің теңдеуін жазыңыз.
в) (2,0) нүктесінен  гиперболасына жүргізілген жанаманың теңдеуін жазыңыз.
гиперболасына жүргізілген жанаманың теңдеуін жазыңыз.
г) Парабола ОХ өсіне симметрия және О(0,0) , М(1,-4) нүктелерінен өтеді. Параболаның теңдеуін жазыңыз.
13. а)А(-1,3), В(0,2), С(1,-1) нүктелерінен өтетін шеңбердің теңдеуін жазыңыз.
б)
Дата добавления: 2015-04-06; просмотров: 240; Опубликованный материал нарушает авторские права?.