Оценка общего качества уравнения линейной регрессии

Относительность оценок параметров и самого уравнения парной регрессии неизбежно ставит проблему качества построенной модели.

Самым общим показателем такого качества, выражающим абсолютную степень отклонения фактических значений результирующей переменной от ее значений, рассчитанных по регрессии, является так называемая остаточная сумма квадратов (сумма квадратов остатков):

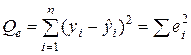где e_i обозначены эмпирические случайные остатки, получаемые после построения уравнения парной регрессии. Величина Q_e прямо зависит от количества наблюдений n.

Другим показателем качества, исключающим влияние числа наблюдений и учитывающим число оцениваемых параметров, является стандартная ошибка парной регрессии (среднеквадратическое отклонение регрессии), которая определяется по формуле:

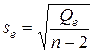. (1.6)

Кроме указанных универсальных показателей качества, применимых к любому типу регрессии, используется также специфичный для парной линейной регрессии показатель - линейный коэффициент парной корреляции.

Коэффициент корреляции r_xy определяет меру тесноты линейной связи между двумя переменными х и у. Существует ряд модификаций формулы для расчета данного коэффициента, например:

(1.7)

или

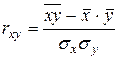, (1.8)

где , - средние квадратичные отклонения переменных x и y, .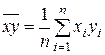

Коэффициент корреляции обладает рядом свойств:

· его значения находятся в интервале от -1 до 1: ;

· близость к нулю абсолютного значения r_xy обычно означает слабую линейную взаимосвязь между переменными; напротив, если абсолютное значение r_xy близко к единице, то это обычно говорит о сильной линейной взаимосвязи между ними;

· если значение r_xy>0 (существенно положительно), то связь между переменными прямая, т.е. с увеличением х значение у также увеличивается; напротив, если значение r_xy<0 (существенно отрицательно), то связь между переменными обратная, т.е. с увеличением х значение у также уменьшается;

· коэффициент корреляции между переменными x и y (r_xy) такой же, как и между переменными y и x (r_yx), т.е. r_xy = r_yx;

· линейные преобразования переменных x и y не изменяют абсолютного значения r_xy. Иначе говоря, если по имеющимся значениям переменных х и у рассчитать значения новых переменных x*=ax+c и y*=by+d, где a,b,c,d – некоторые числа (причем a>0, b>0), то r_xy=r_x_*_y_*.

Кроме того, еще раз подчеркнем, что коэффициент корреляции отражает тесноту именно линейной связи между переменными, т.е. близость его к нулю свидетельствует об отсутствии именно линейной зависимости. Однако при этом переменные могут иметь связь другого вида.

Приведенное выше утверждение о том, что если значение коэффициента корреляции близко к 1 или -1, то переменные тесно взаимосвязаны, справедливо только при достаточно большом объеме статистической выборки. Если число наблюдений мало, то выводы о статистической взаимосвязи весьма сомнительны. Например, при двух наблюдениях значение коэффициента корреляции точно равно единице или минус единице. Однако это вообще ни о чем не свидетельствует.

Доказательство действительной статистической значимости коэффициента корреляции, а, следовательно, и существенность связи между переменными, осуществляется с помощью t-критерия Стьюдента. При этом используется следующий алгоритм:

1) выдвигается гипотеза о случайном характере коэффициента корреляции, т.е. о незначимом его отличии от нуля;

2) на основании найденной оценки r_xy рассчитывается стандартная ошибка коэффициента корреляции s_r по формуле:

;

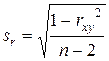3) определяется наблюдаемое значение соответствующей t-статистики:

;

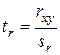4) полученное значение сравнивается с критическим (табличным) значением t_табл, представляющим собой критическую точку распределения Стьюдента для двусторонней критической области с заданным уровнем значимости a и числом степеней свободы k=n-2: t_табл=t(a, n-2).

Если 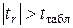, то коэффициент корреляции статистически значим и взаимосвязь между переменными х и у существенная. Это же свидетельствует о значимости линейной регрессии в целом.

Пример 1.2. Используя данные примера 1.1, рассчитаем остаточную сумму квадратов, стандартную ошибку регрессии, коэффициент корреляции.

Таблица 1.2.

Расчет показателей общего качества линейной регрессии

i	x_i	y_i	y_i²
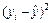
1	2	3	4	5	6
	25,7			50,86	683,30
				60,53	181,44
	23,5			81,26	76,39
				88,17	219,93
	22,5			95,08	357,97
				101,99	728,46
1	2	3	4	5	6
	21,1			114,43	41,34
	19,4			137,92	1855,89
	19,7			133,78	27,25
	20,6			121,34	1,80
	20,2			126,87	97,42
Σ	242,7				4271,19

Значения 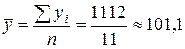, 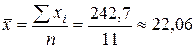. Прогнозируемые значения определяются по формуле .

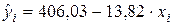Имеем , ,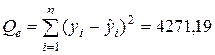

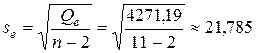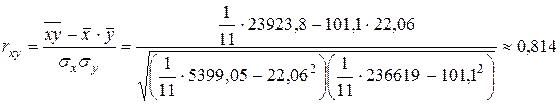Проверим статистическую значимость коэффициента корреляции. Для этого найдем стандартную ошибку s_r:

а затем наблюдаемое значение t-статистики:

Табличное значение t_табл определяем из таблицы критических точек распределения Стьюдента (табл.П.2 приложения). Уровень значимости (уровень ошибки) выбираем равным 0,05. Тогда

t_табл=t(a, n-2)= t(0,05; 9)=2,262.

Как видим, неравенство выполняется. Следовательно, полученный коэффициент корреляции статистически значим, а линейная связь между рассматриваемыми показателями (ценой и объемом продаж яблок) является существенной.

Еще одной общей характеристикой общего качества построенной регрессии (не только парной и линейной, но и любой другой) является средняя ошибка аппроксимации, которая рассчитывается по формуле:

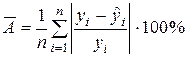Считается [11,14], что если 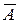не превышает 8-10%, то качество регрессии высокое.

Отметим, что способ оценивания качества регрессии с помощью средней ошибки аппроксимации не всегда оказывается адекватным. Например, если некоторые фактические значения результирующей переменной у равны нулю, то величина 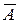становится бесконечно большой. В целом среднюю ошибку аппроксимации не рекомендуется использовать в том случае, когда результирующая переменная в выборке наблюдений принимает значения разных знаков.