IV. Решение неравенств
Пусть функции  и
и  определены на некотором множестве
определены на некотором множестве  . Поставим задачу: найти множество
. Поставим задачу: найти множество  , на котором значения одной из функций больше (меньше) значений другой из них, другими словами, найти все значения
, на котором значения одной из функций больше (меньше) значений другой из них, другими словами, найти все значения  , для которых выполняется неравенство:
, для которых выполняется неравенство:  >
>  (
(  <
<  ).
).
При такой постановке каждое из этих неравенств называется алгебраическим неравенством с неизвестным  .
.
Как при решении уравнения, так и при решении неравенства требуется найти все те значения неизвестной величины, для каждого из которых указанное соотношение оказывается верным. Поэтому естественно и для неравенств ввести понятия, аналогичные тем, которые мы ввели для уравнений.
Множество  называется множеством (областью) допустимых значений неизвестного для данного неравенства.
называется множеством (областью) допустимых значений неизвестного для данного неравенства.
Множество  называется множеством решений данного неравенства.
называется множеством решений данного неравенства.
Решить неравенство – значит найти множество всех  , для которых данное неравенство выполняется.
, для которых данное неравенство выполняется.
Два неравенства называются равносильными, если множества решений их совпадают, т.е. если всякое решение каждого из них является решением другого.
Значение неизвестного называется допустимым для неравенства, если при этом значении обе части неравенства имеют смысл. Совокупность всех допустимых значений неизвестного называется областью определения неравенства.
Основные теоремы преобразования неравенства в равносильное ему:
· Какое-нибудь слагаемое можно перенести из одной части неравенства в другую с противоположным знаком;
· Обе части неравенства можно умножить или разделить на одно и то отличное от нуля положительное число; если это число отрицательное, то знак неравенства меняется на противоположный;
· Если неравенство имеет вид  или
или  , то деление обеих его частей на
, то деление обеих его частей на  , как правило, недопустимо, поскольку может привести к потере решений.
, как правило, недопустимо, поскольку может привести к потере решений.
Между решениями неравенств и уравнений много общего. Отличие же состоит в том, что решением неравенств чаще всего являются бесконечные множества.
Значит, сделать полную проверку ответа, как это делается для уравнений, нельзя. Поэтому очень важно при решении неравенств переходить только к равносильным неравенствам.
К равносильным неравенствам приводят тождественные преобразования, не изменяющие область допустимых значений.
1. Свойства числовых неравенств
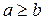  
| пусть 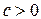 , тогда , тогда
|   
|
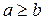 и и   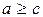
|   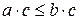
| |
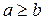  
| пусть  , тогда , тогда
| 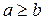  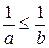
|
  
|
2. Решение неравенств, содержащих квадратный трехчлен:  . Пусть
. Пусть 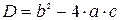 - дискриминант квадратного трехчлена.
- дискриминант квадратного трехчлена.
| Вид неравенства | 
| 
| 
|


|   
|  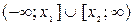
| 
|


|   
|  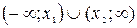
| Решений нет |


|  Решений нет Решений нет
|  
| 
|


| Решений нет |  
| Решений нет |
Если неравенство имеет вид меньше (<) или меньше или равно (£), то можно неравенство умножить на (-1) и свести к виду, приведенному в таблице.
