Общая схема обработки измерений

 

Схему обработки измерений проиллюстрируем на конкретном примере. Предположим, что нам нужно определить ускорение тела, движущегося равноускоренно, без начальной скорости. Выразим ускорение тела из формулы пути для равноускоренного движения:

 

; . (18)

 

Здесь S и t - прямо измеряемые величины, а - косвенно измеряемая величина. Обработку результатов проводим в следующей последовательности:

3.1 Проводим n опытов и получаем n значений S и t. Находим средние значения и

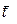
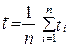; (19)

 

и подставив их в (18), находим среднее значение ускорения

 

(20)

 

3.2 Определяем полную ошибку прямо измеренных величин. Для этого:

3.2.1 Явно сомнительные результаты отбросить как промахи или повторить измерения.

3.2.2 Определить приборные ошибк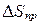и и как половину цены наименьшего деления шкалы или полного наименьшего разряда цифрового прибора.

3.2.3 Рассчитать среднюю случайную ошибку 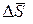и как среднее значения разностей и

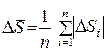; (21)

 

Расчет значени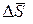й и проводить до того знака после запятой, который фигурирует в соответствующих приборных ошибках 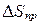и .

3.2.4 Сравнить средние случайные ошибки измерений пути и времени с их
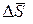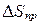приборными ошибками. В качестве полных ошибок ∆S и ∆t взять большие значения и ; и

 

3.3 Расчет погрешностей косвенно измеренной величины производится следующим образом:

3.3.1 Продифференцировать расчетную формулу (20) поочередно по
переменным S и t:

 

(22)

 

 

3.3.2 Так как da≈∆a, ds≈∆s и dt≈∆t, равенство (22) можно записать:

 

(23)

 

3.3.3 Слагаемые со знаком минус по модулю, т.к. ошибки прямо измеренных величин складываются. Вместо ∆S и ∆t подставить их полные ошибки ∆_s и ∆_t.

Тогда формула для расчета абсолютной ошибки прямо измеренной величины а записывается:

, (24)

 

3.3.4 Рассчитать относительную ошибку измерения ускорения по формуле

 

(25)

Примечание. В данном случае связь между a и S и t выражается в виде частного. Поэтому в этом случае проще проводить вычисления вторым способом с предварительным логарифмированием по следующей схеме:

3.4 Прологарифмировать расчетную формулу

 

lna=ln2+lnS-2lnt (26)

 

3.5. Продифференцировать (26) по переменным S и t:

 

(27)

 

3.6 Поменять знак у второго слагаемого и записать (27) в виде

 

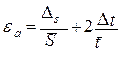(28)

 

3.7 Рассчитать относительную ошибку по формуле (28), а абсолютную, как

(29)

Отметим, что оба способа приводят к одинаковому результату. Например, получим формулу для расчета относительной ошибки 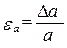, используя формулу (23):

 

(30)

 

Формула (30) аналогичная формуле (27), полученной вторым способом. Однако расчет вторым способом в данном случае проще.