МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
Лабораторная работа № 2.1
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ВОЗДУХА
Цель работы:1)изучение явления внутреннего трения в газах;
2) экспериментальное определение коэффициента вязкости воздуха;
3) оценка средней длины свободного пробега молекул и их эффективного диаметра.
Схема экспериментальной установки
1 – резервуар;
2 – крышка;
3 – кран;
4 – мерный стакан;
5 – секундомер;
6 – трубка;
7 – капилляр;
8 – манометр;
9 – линейка
|
Теория метода
Для определения коэффициента вязкости воздуха в лабораторной работе (рис. 1) используется экспериментальная установка, основные элементы которой выполняют следующие функции.
В резервуар 1 заливается вода, после чего он герметично закрывается завинчивающейся крышкой 2. Для слива воды предназначен кран 3; мерный стакан 4 позволяет контролировать объем сливаемой воды V, а секундомер 5 – время ее истечения t. Воздух в надводной части резервуара сообщается с атмосферой через трубку 6, в свободный конец которой вмонтирован капилляр (очень узкая стеклянная трубка) 7 длиной L. По мере вытекания воды из резервуара его надводный объем увеличивается, что приводит к падению в нем давления воздуха. При возникновении на концах капилляра перепада давлений Dр начинается всасывание воздуха. Для измерения перепада давлений Dр используется манометр 8, представляющий собой U-образную стеклянную трубку с подкрашенной водой. Одно колено манометра сообщается через трубку 6 с воздухом в резервуаре, а другое (открытое) – с атмосферой. Уровни воды в коленах манометра h1 и h2 измеряются с помощью линейки 9.
При понижении давления в резервуаре уровень воды в левом (на схеме) колене повышается, а в правом – понижается, пока давление столба воды Dh = h1 – h2 не уравновесит перепад давлений Dр:
, (1)
где rв – плотность воды; g – ускорение свободного падения.
В установившемся режиме объемный расход воздуха G (объем, протекающий за единицу времени) через капилляр равен объемному расходу вытекающей из резервуара воды:
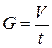. (2)
Очевидно, что величина G тем больше, чем больше перепад давлений Dр и внутренний радиус капилляра r, и тем меньше, чем длиннее капилляр и больше вязкость текущего воздуха h. Количественно взаимосвязь этих величин определяется формулой Пуазейля:
.
С учетом соотношений (1) и (2) эта формула примет вид:
. (3)
Зная геометрические размеры (длину L и радиус r) капилляра и измеряя величины V, t, h1 и h2 , с помощью формулы (3) можно найти коэффициент вязкости воздуха:
.
Значения L, r, g и rв представляют собой константы; если в процессе опытов поддерживать неизменным освобождаемый объем V, то расчетную формулу для коэффициента вязкости можно представить в виде:
, (4)
где
. (5)
Молекулярно-кинетическая теория дает следующее выражение для коэффициента вязкости идеального газа:
, (6)
где r – плотность газа; < l > – средняя длина свободного пробега молекул; <v> – средняя скорость их хаотического (теплового) движения. Из выражения (6) можно найти среднюю длину пробега:
. (7)
Плотность газа выразим из уравнения Менделеева-Клапейрона:
,
откуда
, (8)
где р – давление; V – объем; т – масса газа; m – молярная масса; R –универсальная газовая постоянная; Т – абсолютная температура.
Распределение молекул идеального газа по скоростям (распределение Максвелла) позволяет найти среднюю скорость их теплового движения как
. (9)
Подставляя выражения (8) и (9) в (7), получим
. (10)
В соответствии с теорией, средняя длина свободного пробега < l > молекул идеального газа обратно пропорциональна их концентрации п и эффективному сечению s , т.е. квадрату эффективного диаметра dэ :
,
откуда
.
Учитывая известное соотношение
p = nkT,
где k – постоянная Больцмана, выразим концентрацию молекул через давление газа и его температуру:
;
тогда
. (11)
Порядок измерений и обработки результатов
1. Выпишите в тетрадь геометрические размеры капилляра L и r (спишите с экрана монитора), выразив их в метрах. Используя справочные материалы, спишите значения известных констант g, R, k, а также плотность воды rв . Молярную массу воздуха примите равной m = 0,029 кг/моль. Запишите рекомендуемое значение объема выливаемой из резервуара воды V (на мониторе).
2. Рассчитайте по формуле (5) и запишите в тетрадь значение константы С (в Н/м3).
3. Спишите с экрана монитора данные о параметрах окружающего воздуха.
4. Температуру воздуха Т переведите из градусов Цельсия в кельвины, а давление р – из миллиметров ртутного столба в паскали.
5. Подставьте под кран сливную емкость; откройте кран и следите за уровнями воды в манометре. После установления постоянных уровней подставьте под кран мерный стакан и одновременно включите секундомер. С помощью линейки определите и запишите в таблицу высоту уровней h1 и h2 , выразив эти значения в метрах. В момент наполнения стакана до заданного объема V выключите секундомер и закройте кран. Занесите в таблицу показания секундомера t.
| Номер опыта | h1 , м | h2 , м | t, c | h, мкПа×с | Dh, мкПа×с | (Dh)2, (мкПа×с)2 |
| … | … | … | … | … | … | … |
 =
| s = |
5. Повторите описанный в п. 5 опыт еще четыре раза, стараясь устанавливать различный расход воды из крана (а значит, различный перепад уровней воды в манометре).
6. Для каждого из пяти проделанных измерений вычислите коэффициент вязкости воздуха по формуле (4) и занесите его в таблицу. Для удобства записи и дальнейших расчетов переведите полученные значения в мкПа×с.
7. Найдите среднее значение коэффициента вязкости и занесите его в таблицу. Выполните все расчеты, необходимые для оценки случайной погрешности определения величины h. Задаваясь доверительной вероятностью a = 0,95, рассчитайте погрешность Dsh.
8*. Определите абсолютные приборные ошибки прямых измерений уровней воды d h, радиуса d r и длины d L капилляра, объема выливаемой воды d V и времени ее истечения d t, а также относительные ошибки
.
9*. Найдите абсолютную приборную погрешность косвенного измерения коэффициента вязкости dh. Для этого, если потребуется, используйте формулу
.
10. Оцените полные абсолютную D и относительную Е погрешности. Сделав необходимые округления, запишите окончательный результат измерения коэффициента вязкости воздуха. Сравните полученное значение с табличным.
11. Подставляя в формулу (10) среднее значение коэффициента вязкости (в Па×с), оцените среднюю длину свободного пробега молекул воздуха < l >, а затем по формуле (11) – их эффективный диаметр dэ . Сравните полученные результаты с данными, имеющимися в учебной литературе. Сделайте выводы.
Контрольные вопросы
1. Что называется эффективным диаметром молекул газа?
2. Как зависит эффективный диаметр от температуры и давления?
3. Что называется длиной свободного пробега молекул газа?
4. Как зависит длина свободного пробега от температуры и давления?
5. Что называется вязкостью газов и от каких параметров она зависит?
6. Как объяснить различие температурной зависимости динамической вязкости газов и жидкостей?
7. Получить выражение для определения динамической вязкости газов методом истечения через капилляр.
8. Какие другие методы применяются для определения динамической вязкости жидкостей и газов?
9. Что называется кинематической вязкостью и в каких единицах она измеряется?
10. Какое течение называется ламинарным?
11. Какой физический смысл имеет число Рейнольдса?
12. Произведите вывод формулы Гагена-Пуазейля.
13. Приведите распределение Максвелла молекул идеального газа по скоростям. Обоснуйте основные свойства распределения Максвелла по скоростям.
14. Опишите изменения кривой распределения Максвелла с увеличением температуры.
15. Как из распределения Максвелла получают формулы для наивероятнейшей и средней скорости молекул? Сформулируйте эргодическую гипотезу.
Литература:
[3]- §106, 107, 111, 112; [10]- §6.2, 6.3;
Лабораторная работа № 2.2
ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЕМКОСТЕЙ ГАЗА
МЕТОДОМ АДИАБАТИЧЕСКОГО РАСШИРЕНИЯ
Цель работы:1) изучение первого начала термодинамики в различных изопроцессах;
2) экспериментальное определение показателя адиабаты для воздуха.
Схема экспериментальной установки
1 – сосуд с воздухом;
2 – насос;
3 – манометр;
4 – пробка;
5 – линейка
|
Описание установки
Основной элемент лабораторной установки – сосуд 1 с воздухом, соединенный гибкими шлангами с насосом 2 и манометром 3 (устройство и принцип действия манометра описаны в руководстве к работе 2.1). Сосуд закрыт пробкой 4, вынимая которую можно обеспечить сообщение воздуха в сосуде с атмосферой. Линейка 5 служит для измерения разности уровней в коленах манометра.
Теория метода
В открытом сосуде устанавливаются температура Т1 и давление р1 воздуха, равные соответствующим параметрам окружающей атмосферы. На рис. 2 изображена p-V диаграмма, где это начальное состояние воздуха обозначено точкой 1. Под величиной V здесь и в дальнейшем будем иметь в виду объем достаточно малой массы воздуха (например, 1 г), постоянно находящегося внутри сосуда.
Если сосуд закрыть пробкой и закачать в него из атмосферы некоторое дополнительное количество воздуха, то давление в нем повысится до величины р2 . При достаточно быстром осуществлении этого процесса теплообмен с окружающей средой не успевает происходить, и сжатие можно считать адиабатическим (кривая 1-2). Совершенная внешними силами работа сжатия целиком переходит во внутреннюю энергию газа; следовательно, повышается и его температура. По окончании работы насоса объем газа остается неизменным, и начинается его изохорическое охлаждение до температуры окружающей среды Т1 . На диаграмме этот процесс изображен отрезком 2-3. Понижение температуры при постоянном объеме ведет, как известно, к уменьшению давления до значения р3 , которое все же превышает (из-за ранее накаченного воздуха) атмосферное давление р1 на некоторую величину DрI .
 |
Если теперь открыть сосуд, вынув пробку, и тут же опять закрыть, то давление воздуха в нем сравняется с атмосферным р1 за счет того, что часть воздуха покинет сосуд. Это падение давления происходит очень быстро, и процесс расширения 3-4 также можно считать адиабатическим. Внутренняя энергия газа уменьшается на величину работы расширения, поэтому его температура падает ниже установившегося ранее значения Т1 . Далее воздух в закрытом сосуде нагревается при постоянном объеме до температуры Т1 (на диаграмме – отрезок изохоры 4-5). Установившееся в конце этого процесса давление р5 превышает (вследствие роста температуры) начальное значение р1 на величину DрII .
Рассмотрим подробнее два заключительных процесса: адиабатическое расширение 3-4 и изохорическое нагревание 4-5. Для первого из них запишем уравнение адиабаты:
, (1)
где 
– показатель адиабаты, представляющий собой отношение теплоемкости газа при постоянном давлении Ср к его теплоемкости при постоянном объеме CV .
Учитывая, что в состоянии 4 давление воздуха в сосуде равно атмосферному (р4 = р1), а объем имеет то же значение, что и в конечном состоянии 5 (V4 = V5), перепишем (1) в виде
. (2)
Температура воздуха в состояниях 3 и 5 одинакова и равна температуре окружающей атмосферы Т1 . Воспользовавшись уравнением изотермы
,
находим
,
и уравнение (2) принимает вид
,
откуда показатель адиабаты
. (3)
Преобразуем знаменатель дроби в правой части выражения (3)
, (4)
а также величины давлений р3 и р5 (см. рис. 2):
;
тогда
. (5)
Как известно, атмосферное давление эквивалентно давлению столба воды высотой около 10 м. Перепады давлений, измеряемые в данной работе манометром, составляют величины порядка нескольких сантиметров водного столба. Таким образом, величины DрI и DрII несоизмеримо малы по сравнению с р1 , и отношения
Используем известное в математике соотношение, имеющее место при малых х (х << 1):
ln(1 + x) » x.
Тогда выражения (5) и (4) преобразуются к виду
;
,
а их подстановка в (3) дает
. (6)
Перепад давлений Dр прямо пропорционален разности Dh уровней воды в коленах манометра. С учетом этого выражение (6) примет вид
, (7)
где
; (8)
; (9)
– высота уровня воды в закрытом (на схеме – левом) и открытом (правом) коленах манометра после изохорического охлаждения, т.е. в состоянии 3; 
– то же, после изохорического нагревания (состояние 5).
Порядок измерений и обработки результатов
1. Откройте сосуд 1 с воздухом, вынув пробку 4. Дождавшись установления постоянных одинаковых уровней воды в манометре 3, закройте сосуд.
2. Вращая рукоятку насоса 2, следите за манометром. По достижении разности уровней около 15-20 см прекратите накачивать воздух.
3. Наблюдайте показания манометра в течение двух-трех минут (разность уровней должна уменьшаться). После установления неизменной разности уровней измерьте и занесите в таблицу значения . Рассчитайте по формуле (8) и запишите в таблицу перепад DhI .
| Номер опыта |  , мм
|  , мм
| DhI , мм |  , мм
|  ,
мм
| DhII , мм | g | Dg | (Dg)2 |
| … | … | … | … | … | … | … | … | … | … |
 =
| s = |
4. Вынув пробку, откройте и быстро закройте сосуд. Следите за показаниями манометра (разность уровней должна увеличиваться). Выждав две-три минуты до установки постоянного перепада давлений, измерьте и занесите в таблицу значения ; по формуле (9) рассчитайте и запишите установившуюся разность уровней DhII .
5. Повторите измерения, описанные в пп. 1-4, еще девять раз.
6. Для каждого из десяти проведенных опытов вычислите по формуле (7) и занесите в таблицу значения показателя адиабаты g.
7. Найдите среднее значение показателя адиабаты . Выполните все расчеты, необходимые для оценки случайной погрешности определения величины g. Задаваясь доверительной вероятностью a = 0,95, рассчитайте погрешность Dsg.
8*. Определите абсолютную приборную ошибку прямого измерения высоты уровней воды в манометре d h, а также относительные ошибки
.
9*. Найдите абсолютную приборную погрешность косвенного измерения показателя адиабаты dg. Для этого, если потребуется, используйте формулу
.
10. Оцените полные абсолютную D и относительную Е погрешности. Сделав необходимые округления, запишите окончательный результат измерения показателя адиабаты (отношения теплоемкостей) воздуха.
Контрольные вопросы
1. Каков смысл внутренней энергии идеального газа с точки зрения молекулярно-кинетической теории?
2. Дать определения удельной и молярной теплоемкостей. В каких единицах они измеряются и какова связь между ними?
3. Какой процесс называется адиабатическим? Чему равна работа при адиабатическом процессе?
4. Произведите вывод уравнения Пуассона для адиабаты.
5. Чему равна величина отношения 
для одно-, двух-, трехатомных газов согласно молекулярно-кинетической теории теплоемкости идеальных газов?
6. Вывести уравнение Майера. В чем заключается физический смысл универсальной газовой постоянной?
7. Что такое степень свободы? Показать, что 
.
Литература:
[3]- §101-105; [10]- §1.2, 1.3;
3. ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
Лабораторная работа № 3.1
ИЗУЧЕНИЕ ЗАКОНА ОМА
Цель работы: 1) знакомство с простейшими электрическими схемами и приобретение навыков работы с электро-измерительными приборами;
2) экспериментальная проверка закона Ома для участка электрической цепи.
Схема экспериментальной установки
БП – блок питания:
В – выпрямитель;
П – потенциометр;
V – вольтметр;
K – ключ;
А – миллиамперметр;
R – магазин сопротивлений
Теория метода
Как известно, сила тока на участке цепи прямо пропорциональна напряжению (разности потенциалов) U на этом участке и обратно пропорциональна его сопротивлению R (или прямо пропорциональна величине 
):
. (1)
Выражение (1), хорошо известное как закон Ома для участка цепи, позволяет, в частности, определить сопротивление этого участка по измеренным значениям силы тока и напряжения:
. (2)
Если, не меняя напряжения, измерять силу тока при различных значениях сопротивления, то, согласно (1), напряжение U будет коэффициентом пропорциональности между током I и величиной 1/R. Таким образом, график зависимости I (1/R) должен представлять собой прямую, проходящую через начало координат. Значение напряжения можно найти как тангенс угла наклона этой прямой к оси абсцисс:
. (3)
Источником питания в экспериментальной установке служит переменное (сетевое) напряжение. Выпрямитель В, входящий в состав блока питания БП, преобразует это напряжение в постоянное. Потенциометр П позволяет изменять величину постоянного напряжения U на выходе из блока питания (практически это осуществляется вращением ручки на панели БП). Измеряется величина U вольтметром V, шкала которого также выведена на панель БП.
Исследуемый участок цепи состоит из последовательно соединенных ключа K, миллиамперметра А, служащего для измерения силы тока I, и магазина сопротивлений R (сопротивление миллиамперметра и подводящих проводов пренебрежимо малы).
Порядок измерений и обработки результатов
Упражнение 1. ИЗУЧЕНИЕ ЗАВИСИМОСТИ СИЛЫ ТОКА ОТ НАПРЯЖЕНИЯ
1. Ознакомьтесь с электроизмерительными приборами. Определите класс точности вольтметра KV и миллиамперметра KА , а также их пределы измерения Umax и Imax . Запишите величины KV , KA , Umax и Imax в тетрадь. Рассчитайте цену деления этих приборов
2. Ознакомьтесь с магазином сопротивлений. Определите его класс точности KM и запишите эту величину в тетрадь. Вращением соответствующих ручек (ручку «´1000» не трогать!) установите рекомендуемое значение сопротивления R0 (в пределах от 1000 до 1500 Ом) и также запишите его в тетрадь.
3. Включите в сеть блок питания БП и замкните ключ К.
4. Вращением ручки потенциометра на панели БП установите начальное значение напряжения U = 3 В.
5. Со шкалы миллиамперметра снимите значение силы тока I. Показания приборов (величины U и I ) занесите в соответствующие столбцы табл. 1.
Таблица 1
| Номер опыта | U, B | I , мА | R , Ом | DR , Ом | (DR)2 , Ом2 |
| … | … | … | … | … | … |
| S = | S = |
6. Увеличивая на один вольт значение подаваемого напряжения U, повторите действия, описанные в п. 5, еще четыре раза.
7. Переводя силу тока I в амперы, вычислите по формуле (2) и занесите в таблицу значения сопротивления R для каждого опыта.
8. Рассчитайте сумму найденных значений сопротивления и запишите ее в первую ячейку « S = ». Найдите среднее значение сопротивления 
.
9*. Вычислите и занесите в таблицу отклонения DR каждого из значений сопротивления от среднего, а также квадраты этих отклонений. Сумму квадратов отклонений занесите во вторую ячейку « S = ». Выполните все расчеты, необходимые для оценки случайной погрешности DsR. Найдите величину DsR, задаваясь доверительной вероятностью a = 0,95.
10*. По классу точности и пределу измерения приборов определите абсолютные приборные погрешности измерения напряжения d U и силы тока d I, а также относительные ошибки EU и EI .
11*. Оцените абсолютную приборную погрешность косвенного измерения сопротивления d R. При необходимости воспользуйтесь формулой
.
12*. Оцените полные абсолютную D и относительную Е погрешности. Сделав необходимые округления, запишите окончательный результат измерения сопротивления. Сопоставьте полученный доверительный интервал с установленным значением сопротивления магазина R0.
13*. Вычислите абсолютную приборную ошибку сопротивления магазина
и оцените его доверительный интервал R0 ± d R0 . Сравните его с ранее полученным интервалом. Сделайте выводы о характере зависимости силы тока от напряжения на участке электрической цепи.
Упражнение 2. ИЗУЧЕНИЕ ЗАВИСИМОСТИ ТОКА ОТ СОПРОТИВЛЕНИЯ
1. Ручкой потенциометра установите рекомендуемое значение напряжения U0 . Запишите это значение в тетрадь.
2. Установите на магазине сопротивлений начальное значение R = 1000 Ом.
3. Со шкалы миллиамперметра снимите значение силы тока I. Переведите это значение в амперы. Показания приборов (величины R и I ) занесите в табл. 2.
Таблица 2
| Номер измерения | … | п | ||
| R, Ом | … | |||
| I , A | … | |||
| , Ом – 1
| … |
4. Увеличивая значение сопротивления магазина с помощью ручки «´100» на 100 Ом, повторите действия, перечисленные в п. 3, еще семь раз.
5. Отключите установку от сети.
6. Постройте график зависимости силы тока I от величины . Сделайте вывод о характере зависимости силы тока от сопротивления участка цепи.
7. Проведите сглаживающую прямую через начало координат и экспериментальные точки. Выберите на этой прямой две точки (одной из них может быть начало координат) и по тангенсу угла наклона прямой, используя формулу (3), рассчитайте значение напряжения U.
8. Сравните полученное значение U с ранее записанным показанием вольтметра U0 . Оцените их относительное отклонение
.
Контрольные вопросы
1. Сила тока (определение). Закон Ома для однородного участка цепи.
2. Закон Ома для неоднородного участка цепи.
3. Закон Ома для замкнутой цепи.
4. Закон Ома в дифференциальной форме.
5. Сопротивление проводника. Получить выражение для последовательного и параллельного соединений сопротивлений.
Литература
[4] - §31, 33-35; [7] - §5.1-5.3; [12] - §96-98, 100.
Лабораторная работа № 3.2
ИССЛЕДОВАНИЕ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
Цель работы: 1) экспериментальное нахождение точек заданного потенциала на плоской модели электростатического поля;
2) построение эквипотенциальных и силовых линий поля;
3) расчет характеристик поля по результатам экспериментального исследования.
Схема экспериментальной установки
E – источник постоянной ЭДС;
K – ключ;
R1 – реостат;
V – вольтметр;
R – реохорд;
Г – нуль-гальванометр;
З – зонд;
М – модель.
Для выполнения данной работы необходимо иметь лист милли-метровой бумаги формата А3 и чертежные принадлежности (карандаш, линейку, циркуль и др.)
Теория метода
Питание электрической цепи установки осуществляется от источника постоянной ЭДС; замыкается цепь ключом K. Реостат R1 служит для регулирования подаваемого на установку постоянного напряжения U, а вольтметр – для контроля заданной величины этого напряжения.
Реохорд R представляет собой деревянную линейку с миллиметровыми делениями, по оси которой протянут однородный металлический проводник постоянного сечения и известной длины lcd . Вдоль проводника можно перемещать подвижный контакт е. При замыкании цепи по проводнику течет ток I ; в соответствии с законом Ома
,
где R = Rcd – сопротивление проводника. Напряжение на участке се равно
, (1)
где Rce – сопротивление этого участка.
Очевидно, что наименьшим потенциалом обладает точка с реохорда, непосредственно соединенная с «минусом» источника. Если принять потенциал этой точки равным нулю (j с = 0), то потенциал точки d будет равен U, а потенциал подвижного контакта (точки е) j е = Uce . Учитывая, что сопротивление однородного проводника неизменного сечения прямо пропорционально его длине, можно переписать соотношение (1) в виде
, (2)
где lce – длина участка се, определяемая по делениям реохорда (начало его шкалы должно совпадать с точкой с).
Модель электростатического поля М представляет собой электропроводную бумагу, наклеенную на пластину из диэлектрика и разграфленную координатной сеткой. К бумаге прижаты изготовленные из металла электрод а(« – »), накоротко соединенный с точкой с реохорда, и электрод b (« + »), соединенный с точкой d. Таким образом, при замыкании цепи потенциалы электродов будут равны: j а = j с = 0; j b = j d = U. При наличии постоянной разности потенциалов по бумаге течет постоянный ток. Следовательно, поле модели не является электростатическим. Однако распределение потенциалов точек модели стационарно (постоянно во времени) и не отличается от того, которое сформировалось бы в электростатическом поле. Поэтому данное поле моделирует электростатическое, а наличие проводника (бумаги) между электродами позволяет измерять потенциалы различных его точек.
Для определения потенциалов точек модели, а точнее, для поиска на ней точек с заданным потенциалом, служит участок еЗ электрической цепи. Его главным элементом является гальванометр Г – прибор для обнаружения (при необходимости – и для измерения) малых токов, текущих в различных направлениях. Одна из клемм гальванометра соединена с подвижным контактом (точкой е) реохорда, а к другой подключен металлический зонд З. Предположим, что цепь замкнута, и потенциал точки е известен. Если коснуться зондом электрода а модели, то через гальванометр потечет ток в направлении от е к З, т.к. j е > j a = 0. Если же коснуться зондом электрода b, то направление тока будет противоположным, т.к. j е < j b = U. Потенциал j произвольно выбранной точки модели лежит в пределах 0 < j < U. Очевидно, что между электродами найдутся и такие точки, потенциал которых j = j е (совокупность этих точек представляет собой эквипотенциальную линию – сечение эквипотенциальной поверхности плоскостью модели). Перемещая зонд по модели, можно «нащупать» одну из таких точек; при этом разность потенциалов на участке еЗ, а следовательно, и ток через гальванометр будут равны нулю. В этом и заключается поиск точек заданного потенциала в поле модели; отсюда происходит название прибора – «нуль-гальванометр». Наличие координатной сетки позволяет нанести найденные точки на чертеж (миллиметровую бумагу) и, соединив их между собой, построить эквипотенциальную линию. Изменяя положение подвижного контакта реохорда и рассчитывая новые значения потенциала точки е по формуле (2), можно получить семейство нескольких линий равного потенциала. Это дает возможность, во-первых, изобразить силовые линии поля; во-вторых, рассчитать значение напряженности поля в любой его точке.
Вектор напряженности 
связан с потенциалом электростатического поля известным соотношением
, (3)
где gradj – градиент потенциала. Из этого соотношения следует, что напряженность направлена в сторону наискорейшего убывания потенциала, т.е. силовые линии поля нормальны (перпендикулярны) к эквипотенциальным поверхностям и направлены «от плюса к минусу».
 |
В случае одномерного поля потенциал зависит лишь от одной координаты r : j = j (r). На модели такого поля электроды имеют одинаковую правильную геометрическую форму. Это либо параллельные друг другу отрезки (в этом случае ось Or направлена перпендикулярно электродам), либо концентрические окружности (при этом ось Or совпадает с радиальной прямой). Эквипотенциальные линии повторяют по форме очертания электродов, а силовые линии представляют собой семейство прямых – параллельных или радиальных – и направлены от положительного электрода к отрицательному. В одномерном поле векторное соотношение (3) в проекции на ось Or принимает вид:
. (4)
Как известно, значение производной функции в заданной точке (r = r0) численно равно угловому коэффициенту (тангенсу угла a наклона к оси абсцисс) касательной, проведенной в этой точке к кривой, изображающей график функции. Рис. 2 иллюстрирует графический способ определения проекции вектора напряженности Er . Выбрав на касательной две точки 1 и 2 (они должны располагаться как можно дальше друг от друга и могут совпадать с точками пересечения прямой и осей координат), найдем угловой коэффициент:
.
Согласно (4),
или
. (5)
Порядок измерений и обработки результатов
1. Ознакомьтесь с элементами лабораторной установки и измерительными приборами. Запишите в тетрадь длину реохорда lcd , выразив ее в миллиметрах.
2. На миллиметровой бумаге изобразите в масштабе 1:1 модель электростатического поля (электроды и координатные оси с делениями).
3. Введите реостат R1 полностью (установите его движок так, чтобы сопротивление реостата было максимальным).
4. Замкните ключ K.
5. Перемещая движок реостата R1 и наблюдая за показаниями вольтметра, установите рекомендуемое значение напряжения U. Запишите это значение в тетрадь.
6. Руководствуясь рекомендациями, установите подвижный контакт (ползунок) е реохорда в начальное положение.
7. Значение длины участка lce (в миллиметрах) занесите в таблицу. По формуле (2) рассчитайте потенциал jе , равный потенциалу j точек искомой эквипотенциальной линии модели, и запишите его значение в соответствующий столбец таблицы.
| Номер линии | lce , мм | j, В | Номер точки | х, мм | у, мм | r, м |
| … | … | … | … | |||
| п | ||||||
| Среднее значение r : | ||||||
| … | … | … | … | |||
| п | ||||||
| Среднее значение r : | ||||||
| … | … | … | … | … | … | … |
| N | ||||||
| … | … | … | … | |||
| п | ||||||
| Среднее значение r : |
8. Коснитесь зондом З точки модели вблизи отрицательного электрода а. Запомните направление, в котором «зашкаливает» стрелка гальванометра Г. Коснувшись точки ближе к положительному электроду b, убедитесь в том, что направление «зашкаливания» изменилось на противоположное. Затем коснитесь третьей точки, расположенной между двумя первыми. Сужая, таким образом, зону поиска, найдите точку, касание которой обращает показания гальванометра в нуль (практически стрелка прибора должна при этом установиться или совершать малые колебания в пределах его шкалы). Используя сетку модели, определите координаты х и у найденной точки и запишите их в таблицу. Нанесите эту точку на миллиметровую бумагу.
9. Повторите действия, описанные в п. 8, не менее семи раз (n ³ 8). Найденные точки должны быть расположены достаточно далеко друг от друга в поле всей модели – так, чтобы по ним можно было построить эквипотенциальную линию. В соответствии с рекомендациями переместите ползунок е реохорда в следующее положение.
10. Повторяя пп. 7-9, снимите данные для построения N эквипотенциальных линий (число N ³ 4 определяется количеством рекомендуемых положений ползунка реохорда). Точки, имеющие различные значения потенциала, при перенесении на миллиметровую бумагу желательно обозначать по-разному (пустые и заштрихованные кружки, крестики, ромбы и т.п.).
11. Исходя из формы электродов модели, выберите направление оси Or вдоль силовых линий поля (подсказка: для «прямоугольных» моделей ось Or совпадает с осью Oх (r º x), а для «круглых» – направлена от центра и 
). Определите значения координаты r найденных точек и, выразив их в метрах, занесите в последний столбец таблицы.
12. Для каждой эквипотенциальной линии вычислите среднее значение координаты r и запишите его в соответствующую ячейку таблицы. Используя эти средние значения, постройте на чертеже (милли-метровой бумаге) линии равного потенциала.
13. Изобразите на чертеже силовые линии электростатического поля.
14. На график зависимости потенциала j от координаты r нанесите экспериментальные точки и проведите по ним сглаживающую кривую или прямую.
15. В указанной преподавателем точке поля найдите потенциальную энергию заданного заряда, а также величину действующей на него силы. Направление силы покажите на чертеже стрелкой. Рассчитайте работу перемещения этого заряда в другую указанную точку поля. Для определения потенциалов точек используйте график зависимости j (r); для нахождения проекции вектора напряженности примените графический способ.
Контрольные вопросы
1. Электростатическое поле. Напряженность и потенциал (физический смысл). От чего зависят напряженность и потенциал данной точки поля?
2. Графическое изображение поля. Силовые линии и эквипотенциальные поверхности. Одномерное поле. Однородное поле.
3. Работа сил электростатического поля. Связь между напряженностью и потенциалом.
4. Сформулировать теорему Остроградского-Гаусса для напряженности электрического поля.
5. Рассчитать электрическое поле заряженного шара, бесконечной тонкой нити, бесконечной плоскости.
Литература:
[4] - §1, 5, 6, 8, 12-14; [7] - §1.1-1.6; [12] - §77, 79, 81-86.
Лабораторная работа № 3.3
ОПРЕДЕЛЕНИЕ ГОРИЗОНТАЛЬНОЙ СОСТАВЛЯЮЩЕЙ
ИНДУКЦИИ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
Цель работы: 1) практическое изучение магнитного поля кругового тока и принципа суперпозиции полей;
2) экспериментальное определение горизонтальной составляющей магнитного поля Земли.
Схема экспериментальной установки
ТГ – тангенс-гальванометр;
К – компас;
П – переключатель;
А – миллиамперметр;
R – реостат;
U – источник постоянного напряжения
Теория метода
Основным элементом лабораторной установки является тангенс-гальванометр ТГ, представляющий собой короткую катушку сравнительно большого радиуса r, витки которой расположены в вертикальной плоскости. В центре катушки на специальной горизонтальной площадке находится компас К. Катушка состоит из N витков провода, концы которого подсоединяются через переключатель П к цепи источника постоянного напряжения U. Как видно из схемы, установка контакта переключателя в среднее положение оставляет цепь разомкнутой, а фиксация его в левом и правом положениях замыкает цепь, причем направление тока через катушку в этих случаях будет противоположным. Для изменения величины тока в цепь источника включен реостат R, а для измерения силы тока служит миллиамперметр А.
Как известно, протекание тока по проводнику создает в окружающем пространстве магнитное поле. Так как длина катушки во много раз меньше ее радиуса r, ее можно рассматривать как один круговой виток, по которому течет ток Iв , равный
Iв = N×I, (1)
где I – сила тока во внешней (по отношению к катушке) цепи. Из закона Био-Савара-Лапласа следует, что индукция магнитного поля 
в центре кругового витка радиусом r при протекании по нему тока Iв равна по модулю
, (2)
где m0 – магнитная постоянная; m – относительная магнитная проница-емость среды. В воздухе m » 1; таким образом, с учетом соотношения (1) формула (2) примет вид
. (3)
В дальнейшем величину Вк будем называть индукцией магнитного поля катушки. Направление вектора связано с направлением тока правилом правого винта (буравчика), т.е. направлен вдоль оси катушки.
Когда электрическая цепь разомкнута, магнитная стрелка компаса К находится под воздействием единственного внешнего магнитного поля – поля Земли. При этом стрелка ориентирована вдоль магнитного меридиана, совпадающего с направлением горизонтальной составляющей 
индукции магнитного поля Земли. Перед началом измерений необходимо установить плоскость катушки параллельно магнитному меридиану; в этом случае направление стрелки перпендикулярно оси катушки.
При замыкании цепи по катушке течет ток, и магнитная стрелка оказывается под влиянием двух полей: поля Земли с индукцией и поля катушки с индукцией . Согласно принципу суперпозиции индукция 
результирующего магнитного поля равна
.
Стрелка компаса ориентируется в направлении результирующего поля, т.е. отклоняется от первоначального направления на некоторый угол j (рис. 1). На рис. 2 показано взаимное расположение векторов , и в горизонтальной плоскости, проходящей через центр катушки. При условии начальной ориентации плоскости катушки параллельно магнитному меридиану векторы и взаимно перпендикулярны; как видно из рисунка, их модули в этом случае связаны соотношением
Вк = В0 tgj ,
откуда, с учетом (3),
. (4)
Таким образом, с помощью тангенс-гальванометра можно экспериментально определить величину горизонтальной составляющей индукции магнитного поля Земли. Для этого необходимо знать радиус r и число витков N катушки, а также измерить силу тока I и соответствующий угол j отклонения магнитной стрелки.
С целью получения более достоверного результата следует повторить опыт несколько раз при различных значениях силы тока I. При этом величины m0 , N и r не изменяются, и формулу (4) целесообразно представить в виде
, (5)
где
. (6)
Точно установить плоскость катушки параллельно магнитному меридиану практически невозможно. Для того, чтобы уменьшить возникающую из-за этого ошибку, нужно при одной и той же величине тока I измерять углы отклонения стрелки j 1 и j 2 , соответствующие противоположным направлениям тока через катушку, а в формулу (5) подставлять среднее значение угла
. (7)
Порядок измерений и обработки результатов
1. Ознакомьтесь с лабораторной установкой. Запишите в тетрадь значения радиуса катушки r (в метрах) и числа витков N. По формуле (6) рассчитайте константу С; ее значение (в Гн/м2) также запишите в тетрадь.
2. Определите класс точности КА , предел измерения Imax и цену деления миллиамперметра. Научитесь снимать показания этого прибора. Рассчитайте абсолютную приборную погрешность измерения силы тока d I. Значения КА , Imax и d I запишите в тетрадь.
3. Определите цену деления компаса и научитесь снимать углы отклонения стрелки в обоих направлениях от нулевого деления. Оцените абсолютную приборную погрешность dj и, выразив ее в радианах, запишите в тетрадь.
4. Освободите стрелку компаса. Поверните плоскость катушки так, чтобы стрелка компаса установилась на нулевом делении.
5. Введите реостат R полностью. Замкните контакт переключателя в положение 2. Перемещая движок реостата и наблюдая за показаниями компаса, установите рекомендуемое значение угла поворота стрелки j 1 . По показаниям миллиамперметра определите соответствующее значение силы тока I. Не меняя величины тока, измените его направление, перекинув контакт переключателя в противоположное положение (положение 1). Определите угол отклонения j 2 . Значения I (в амперах), j 1 и j 2 (в градусах) занесите в соответствующие столбцы таблицы.
| Номер опыта | I, A | j 1 , град. | j 2 , град. | j , град. | tgj | В0 , мкТл | DВ0 , мкТл | (DВ0 )2, (мкТл)2 |
| … | … | … | … | … | … | … | … | … |
| п | ||||||||
| S = | S = |
6. Увеличивая значение угла j 1 на заданную величину, повторите действия, описанные в п. 5, не менее шести (п ³ 7) раз.
7. Используя выражение (7), для каждого опыта найдите среднее значение угла поворота j ; с помощью микрокалькулятора или таблиц определите tgj . Результаты запишите в таблицу.
8. По формуле (5) вычислите для каждого из опытов величину горизонтальной составляющей индукции магнитного поля Земли В0 и занесите ее в таблицу, выразив в мкТл.
9. Определите среднее значение 
.
10*. Выполните все расчеты, необходимые для оценки случайной погрешности измерения DsB0 . Найдите величину DsB0 , задаваясь доверительной вероятностью a = 0,95.
11*. Оцените абсолютную приборную погрешность косвенного измерения d В0 по формуле
.
12*. Оцените полные абсолютную D и относительную Е погрешности. Сделав необходимые округления, запишите окончательный результат измерения.
Контрольные вопросы
1. Магнитное поле. Характеристики магнитного поля. Принцип суперпозиции.
2. Закон Био-Савара-Лапласа.
3. Расчет индукции магнитного поля кругового тока, бесконечного прямолинейного проводника с током.
4. Закон полного тока.
5. Поток магнитного поля. Индуктивность.
Литература:
[4] - §40, 42, 47, 48, 50; [7] - §6.1-6.6; [12] – §109, 110, 115, 116, 126.
Лабораторная работа № 3.4
ИЗУЧЕНИЕ МАГНИТНЫХ СВОЙСТВ ФЕРРОМАГНЕТИКОВ
Цель работы: снятие основной кривой намагничивания и петли гистерезиса ферромагнетика.
 |
Схема экспериментальной установки
U – источник постоянного напряжения; Т – тумблер;
Р – потенциометр; R – реостат; А – амперметр; П – переключатель;
L – соленоид; F – ферромагнитный сердечник; K – компас
Теория метода
Питание лабораторной установки осуществляется источником постоянного напряжения U; для замыкания цепи служит тумблер (выключатель) Т. Потенциометром Р можно регулировать подаваемое на установку напряжение, а реостатом R – силу тока в цепи. Для измерения тока в цепь включен амперметр А. С помощью переключателя П можно изменять направление тока через соленоид. Соленоид L представляет собой длинную прямую катушку, в которую помещается исследуемый образец (сердечник) – стержень F из ферромагнитного сплава.
Протекание тока I по виткам соленоида создает внутри него практически однородное магнитное поле, напряженность 
которого равна по модулю
, (1)
где п – число витков, приходящееся на единицу длины соленоида. Индукция магнитного поля , в отличие от напряженности, зависит от свойств среды:
= m×m0× , (2)
где m0 – магнитная постоянная; m – относительная магнитная проницаемость среды.
Рис. 1 Рис. 2
При помещ