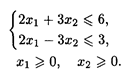Решить задачу линейного программирования графическим методом.
Методические указания по выполнению контрольной работы
По дисциплине
«МЕТОДЫ ОПТИМАЛЬНЫХ РЕШЕНИЙ»
для направления «ЭКОНОМИКА»
бакалавриат
Пермь, 2015
- Структура контрольной работы
Контрольная работа состоит из одного теоретического вопроса и трех задач линейного программирования, решаемых:
1) графическим методом
2) симплексным методом
3) распределительным методом (транспортная задача).
Номера вопросов и задач выбираются в соответствии с вариантом.
Номер варианта равен номеру студента в списке группы.
Контрольная работа высылаются в адрес Академии по почте для регистрации в деканате ЗО и ПК.
Теоретические вопросы
1. Постановка общей задачи математического программирования.
2. Безусловный экстремум.
3. Необходимые и достаточные условия локального экстремума
4. Условный экстремум.
5. Функция Лагранжа для случая уравнения связи в виде единственного равенства.
6. Элементы аналитической геометрии в n-мерном пространстве.
7. Графический метод решения задачи ЛП.
8. Виды двойственных задач и составление их математических моделей
9. Основные теоремы двойственности
10. Экономический анализ задач с использованием теории двойственности.
11. Задача о назначениях
12. Постановки задачи целочисленного программирования.
13. Метод Гомори.
14. Линейное программирование с параметрами в целевой функции.
15. Линейное программирование с параметрами в объемах ограничений.
16. Общая постановка задачи нелинейного программирования.
17. Задача с линейной (нелинейной) целевой функцией и нелинейной (линейной) системой ограничений
18. Дробно-линейное программирование.
19. Метод множителей Лагранжа.
20. Классические и производные критерии принятия решений в условиях полной неопределенности.
21. Составные критерии принятия решений.
22. Классические критерии принятия решений в условиях риска.
23. Методы сравнения рисковых альтернатив.
24. Метод дерева решений.
25. Стратегии безрисковых решений.
26. Метод принятия решений при страховании рисков.
27. Методы анализа риска финансового рычага при принятии кредитных решений.
28. Методы принятия решений на основе концепции полезности.
29. Прямые методы оптимизации решений при многих критериях.
30. Метод анализа иерархий для принятия многокритериальных решений.
Контрольная задача 1
Решить задачу линейного программирования графическим методом.
1. L() = 3x1 + х2→ max при ограничениях:
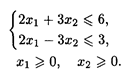
2. L() = 2x1 — 10x2 → min при ограничениях:

3. L() = 2x1 + 3x2 → max при ограничениях:
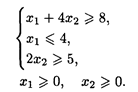
4. L() = 3x1 + 5х2→ max при ограничениях:
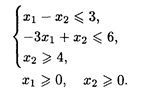
5. L() = 4x1 + 6x2 → min при ограничениях:
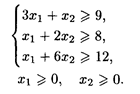
6. L() = 4x2 → min при ограничениях:
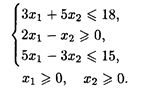
7. L() = 2x1 + 3x2 → max при ограничениях:

8. L() = 2x1 + 3x2 → max при ограничениях:
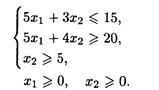
9.L() = x1 + 2x2 → max при ограничениях:
-x1+x2 ≤4
2x1+x2≥6
X2≥2
X1≤5
10. L() = 2x1 + 3x2 → max при ограничениях:

11.L() = 2x1 + 3x2 → max при ограничениях:
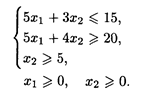
12. L() = 2x1 + 3x2 → max при ограничениях:
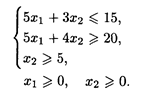
13. L() = 2x1 + 3x2 → max при ограничениях:

14. L() = 2x1 + 3x2 → max при ограничениях:

15. L() = 2x1 + 3x2 → max при ограничениях:

16. L() = 2x1 + 3x2 → max при ограничениях:
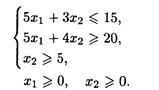
17 . L() = 3x1 + х2→ max при ограничениях:
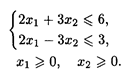
18. L() = 3x1 + 5х2→ max при ограничениях:

19. L() = 4x1 + 6x2 → min при ограничениях:
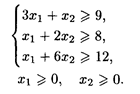
20. L() = 4x2 → min при ограничениях:
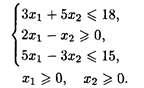
21. L() = 2x1 + 3x2 → max при ограничениях:
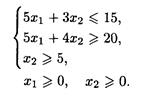
22. L() = 2x1 + 3x2 → max при ограничениях:
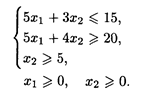
23 L() = x1 + 2x2 → max при ограничениях:
-x1+x2 ≤4
2x1+x2≥6
X2≥2
X1≤5
24. L() = 2x1 + 3x2 → max при ограничениях:

25.L() = 2x1 + 3x2 → max при ограничениях:

26. L() = 2x1 + 3x2 → max при ограничениях:

27. L() = 2x1 + 3x2 → max при ограничениях:
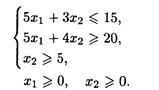
28. L() = 2x1 + 3x2 → max при ограничениях:
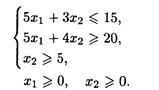
29.L() = x1 + 2x2 → max при ограничениях:
-x1+x2 ≤4
2x1+x2≥6
X2≥2
X1≤5
30 . L() = 3x1 + х2→ max при ограничениях: