Базовая модель Солоу (без технического прогресса)

Рассмотрим «однопродуктовую» экономику в модели Роберта Солоу. Пусть в этой экономике действует репрезентативный потребитель, который одновременно является производителем и владельцем факторов производства (экономика «Робинзона Крузо»). В экономике есть всего два фактора производства: труд и капитал, а выпуск в каждый момент времени t определяется производственной функцией: Y_t = F(K_t,L_t), где F – производственная функция с постоянной отдачей от масштаба. Будем считать, что функция F возрастает по все аргументам, вогнута и удовлетворяет следующим техническим условиям: и

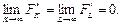
Будем рассматривать закрытую экономику без государственного сектора. Произведенная продукция в момент t может быть использована либо на потребление (C_t), либо на инвестиции (I_t):

Y_t =C_t + I_t (8.7)

 

Полученный доход потребитель распределяет между потреблением (C_t) и сбережениями (S_t), причем будем считать, что сбережения являются некой фиксированной долей дохода:

S_t= sY_t, 0 ≤ s≤1. (8.8)

 

Через s обозначена норма сбережения, не зависящая от дохода и момента времени t, то есть s – экзогенный параметр. Итак, Y_t =C_t + S_t, откуда с учетом (8.7) и (8.8) получаем:

I_t = S_t = sY_t. (8.9)

 

Будем считать, что капитал изнашивается с течением времени, и обозначим через δ (0 ≤ δ ≤ 1) норму амортизации капитала, полагая ее постоянной. Таким образом, валовые инвестиции равны сумме чистого прироста капитала и амортизационных расходов: где – чистый прирост капитала. Подставляя выражение для инвестиций в (8.9), получаем:

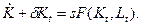(8.10)

 

Будем считать, что население в рассматриваемой экономике равно трудовым ресурсам и растет с постоянным темпом n: L_t = L₀ e^nt. Будем также считать, что в экономике имеет место полная занятость, то есть труд, стоящий в производственной функции, равен имеющимся трудовым ресурсам.

Поделим обе части уравнения (8.10) на L_tи с учетом однородности первой степени функции F получим:

(8.11)

 

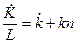Перейдем от абсолютных величин к величинам на одного рабочего, обозначив через k капитал на одного рабочего или фондовооруженность (k ≡K/L), а через f(k)– выпуск на одного рабочего или производительность труда (f(k)≡F(K/L,1)). Тогда откуда находим и подставляем в (8.11):

(8.12)

 

Дифференциальное уравнение (8.12) называют уравнением накопления капитала. В левой части уравнения – чистый прирост капитала на душ населения. Если сбережения на душу населения превышают инвестиции, необходимые для поддержания неизменной величины капитала на душу населения, то эти избыточные средства позволят увеличить запас капитала на душу населения.