Решение.

рН = - lg[Н⁺] = -lg(2×10^-2) = 1.70

Решая обратную задачу, по известному значению рН легко найти концентрации водородных и гидроксид-ионов.

Пример 2. Вычислить [Н⁺] и [ОН^-] раствора, рН которого равен 10.33.

Решение.

[Н⁺] = 1×10^-10.33 = 4.7×10^-11 М.

рОН = 14 - 10.33 = 3.67.

[ОН^-] = 1×10^-3.67 = 2.1×10^-4 М.

 

Сильные кислоты (НХ) и сильные основания (МОН) в водных растворах практически полностью диссоциированы.

HX = H+ + X-	(1.12)
MOH = M+ + OH-	(1.13)

Концентрации Н⁺ и ОН^- в этих растворах в первом приближении можно считать равными общей концентрации С_А кислоты (НХ) и соответственно основания (МОН). Следовательно,

pH = -lgCHX	(1.14)
pOH = -lgCMOH	(1.15)

Эти выражения являются приближенными. В более строгих расчетах концентрацию электролитов следует заменять активностью ионов. Между концентрацией иона и активностью его существует следующая зависимость:

aA = γA×CA

(1.16)

где γ_A - коэффициент активности. Коэффициент активности зависит от ионной силы раствора (μ)

(1.17)

где 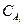- концентрации ионов - катионов и анионов (М), - заряды ионов.

Если 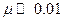, коэффициент активности в водных растворах рассчитывается по формуле

(1.18)

При 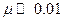расчет проводится по более сложному уравнению

(1.19)

Для сильных электролитов только в очень разбавленных растворах (~ 0.0001 М) γ_A = 1 и а_А = С_А. Коэффициент активности можно не учитывать также для недиссоциированных молекул.

Для простоты расчетов в дальнейшем во всех случаях, кроме оговоренных, вместо активностей используются концентрации.

 

Пример 3. Вычислить рН 0.0018%-ного раствора хлороводородной кислоты.

Решение. Найдем концентрацию НС1, выраженную в М, учитывая, что молекулярная масса НС1 36.46:

рН = - lg(4.94×10^-4) = 3.31.

Пример 4.В 250 мл раствора содержится 0.1 г гидроксида натрия. Вычислить рН раствора.

Решение. Найдем концентрацию NaOH, выраженную в моль/л. Молекулярная масса NaOH 40.

Ионная сила 0.01 М раствора гидроксида натрия равна:

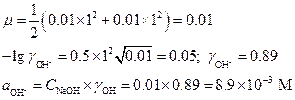
pOH = -lg(8.9×10^-3) = 2.05

pH = 14-2.05 = 11.95

 

Пример 5. К 3 л воды прибавлен 1 г HNO₃ (ρ = l.4). Вычислить рН раствора.

Решение. По таблицам находим, что в 100 г азотной кислоты (ρ = 1.4) содержится 65.3 г HNO₃. Тогда концентрация HNO₃ в М будет равна

pH = -lg(3.4×10^-3) = 2.47

 

В случае слабых кислот константа равновесия реакции {1.2) может быть выражена следующим уравнением:

(1.20)

где К_а - константа диссоциации кислоты НА.

Если общую концентрацию кислоты обозначить С_НА, а равновесную [НА], то

[НА] = СНА - [Н+].

(1.21)

Из уравнения (1.2) следует, что [Н⁺] = [А^-]. Тогда выражение константы диссоциации слабой кислоты можно записать следующим образом:

(1.22)

Отсюда легко найти концентрацию [Н⁺]

(1.23)

Если кислота диссоциирована в незначительной степени ( 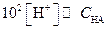), то приближенно можно считать, что.

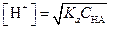
	(1.24)
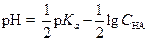
	(1.25)

Слабое основание, как и слабая кислота, в водных растворах диссоциирует неполностью

(1.26)

как и для слабой кислоты,

[BOH] = СBOH - [OН-].

(1.27)

Поскольку [В⁺] = [ОН^-], уравнение для константы диссоциации слабого основания будет иметь вид

(1.28)

и

(1.29)

Когда [OH^-] << С_вон (10² [ОН^-] < С_вон), можно принять

	(1.30)
	(1.31)
	(1.32)

Пример 6.Вычислить рН 0.017 М раствора муравьиной кислоты.

Решение.

 

C_HCOOH = 0. = 1.7×10^-2 М

рН = -lg(1.7×10^-3 ) = 2.76.

Пример 7.Вычислить рН 0.06 М раствора аммиака.