Теоретическая стойкость шифров: совершенные шифры.
При рассмотрении вопроса о теоретической стойкости шифров отвлекаются от реальных временных и сложностных затрат по вскрытию шифра (что определяет подход к практической стойкости). Во главу угла ставится принципиальная возможность получения некоторой информации об открытом тексте или использованном ключе. Впервые такой подход исследовал К. Шеннон ([Шен63]). Он рассматривал уже знакомую нам модель шифра и единственную криптоатаку на основе шифртекста. Проследим за его рассуждениями.
Как мы указывали, конечной целью работы криптоаналитика является текст сообщения или ключ шифрования. Однако весьма полезной может быть даже некоторая вероятностная информация об открытом тексте. Например, уже предположение о том, что открытый текст написан по-английски, предоставляет криптоаналитику определенную априорную информацию об этом сообщении даже до того, как он увидит шифртекст. Так, например, он заранее знает, что слово «hello» является более вероятным началом сообщения, чем, скажем, набор букв «abode». Поэтому первая цель криптоанализа состоит в том, чтобы увеличить количество этой априорной информации, относящейся к каждому возможному открытому тексту таким образом, чтобы истинный открытый текст сделать более вероятным после получения шифртекста, хотя, конечно, и не обязательно точным.
Пусть, например, криптоаналитик перехватил текст «abccd» и знает (или предполагает), что он был зашифрован при помощи шифра простой замены. Этот шифртекст говорит ему о том, что открытый текст состоит из пяти букв, третья и четвертая из которых являются одинаковыми, а остальные отличными от этой буквы и разными. Хотя он не может быть уверенным, что этим словом является «hello» (это может быть еще «lessy» или что-то подобное), тем не менее апостериорные вероятности таких открытых текстов возрастают относительно их априорных вероятностей. Криптоаналитик, кроме того, полностью уверен (в предположении, что использовалась именно простая замена) в том, что этот открытый текст не может быть ни словом «after», ни словом «catch», и, таким образом, апостериорная вероятность обоих этих открытых текстов сокращается до нуля, даже вне зависимости от их априорных вероятностей.
Шеннон назвал шифр совершенным, если для любого открытого текста знания, которые могут быть получены из соответствующего ему шифртекста, не раскрывают никакой информации об открытом тексте, за исключением, возможно, его длины. Другими словами, для совершенных шифров апостериорные вероятности открытых текстов (вычисленные после получения криптограммы) совпадают с их априорными вероятностями.
Вспомним о введенной нами модели шифра  , в которой фигурировали распределения вероятностей Р(Х), Р(К). Они как раз и являются наборами априорных вероятностей
, в которой фигурировали распределения вероятностей Р(Х), Р(К). Они как раз и являются наборами априорных вероятностей 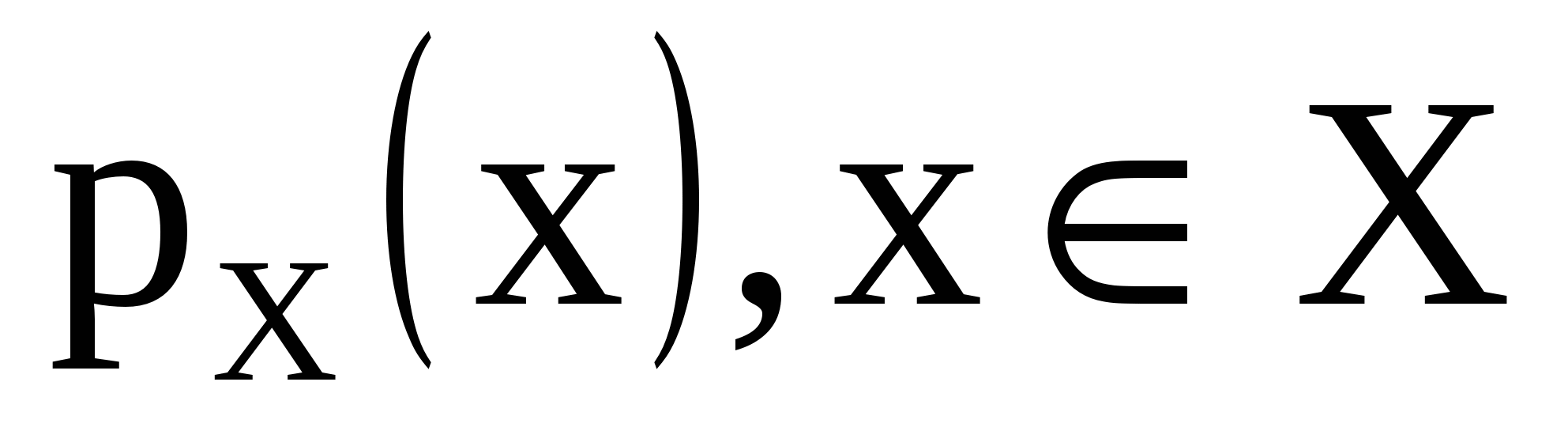 и
и  . Будем предполагать, что рX (х) > 0, рK (k) > 0 для любых х
. Будем предполагать, что рX (х) > 0, рK (k) > 0 для любых х  X, k
X, k  К.
К.
Далее мы будем рассматривать лишь такие шифры, для которых выбор ключа и выбор открытого текста являются независимыми событиями. Это равносильно тому, что распределения Р(Х), Р(К) являются независимыми. Эти распределения естественным образом индуцируют распределение вероятностей P(Y) =  на множестве возможных шифртекстов по формуле
на множестве возможных шифртекстов по формуле
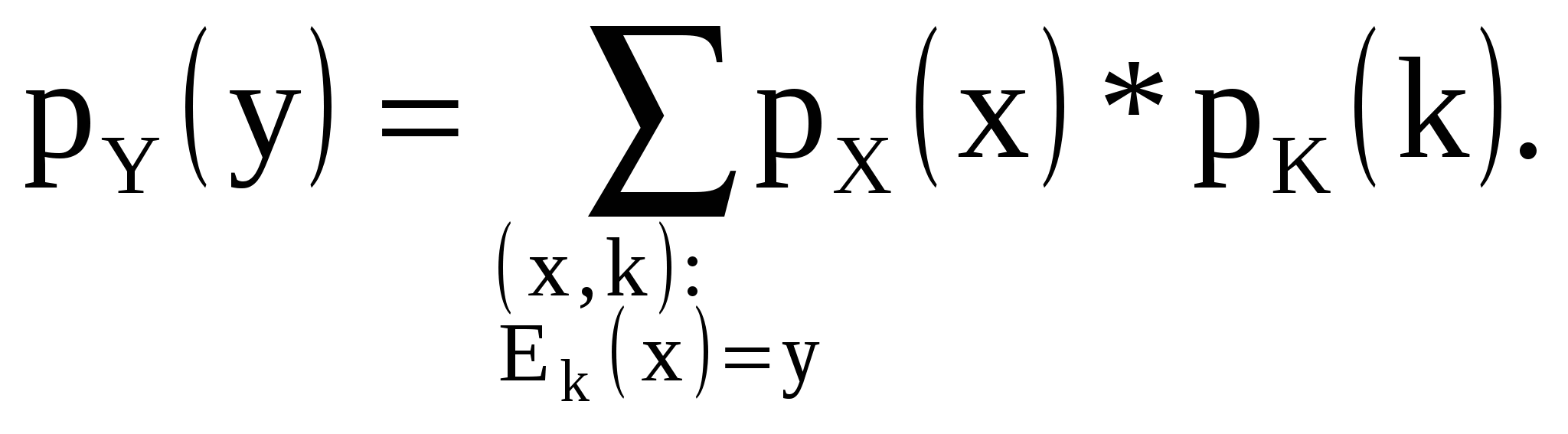 (14)
(14)
Поясним корректность такого определения. Нужно проверить, что
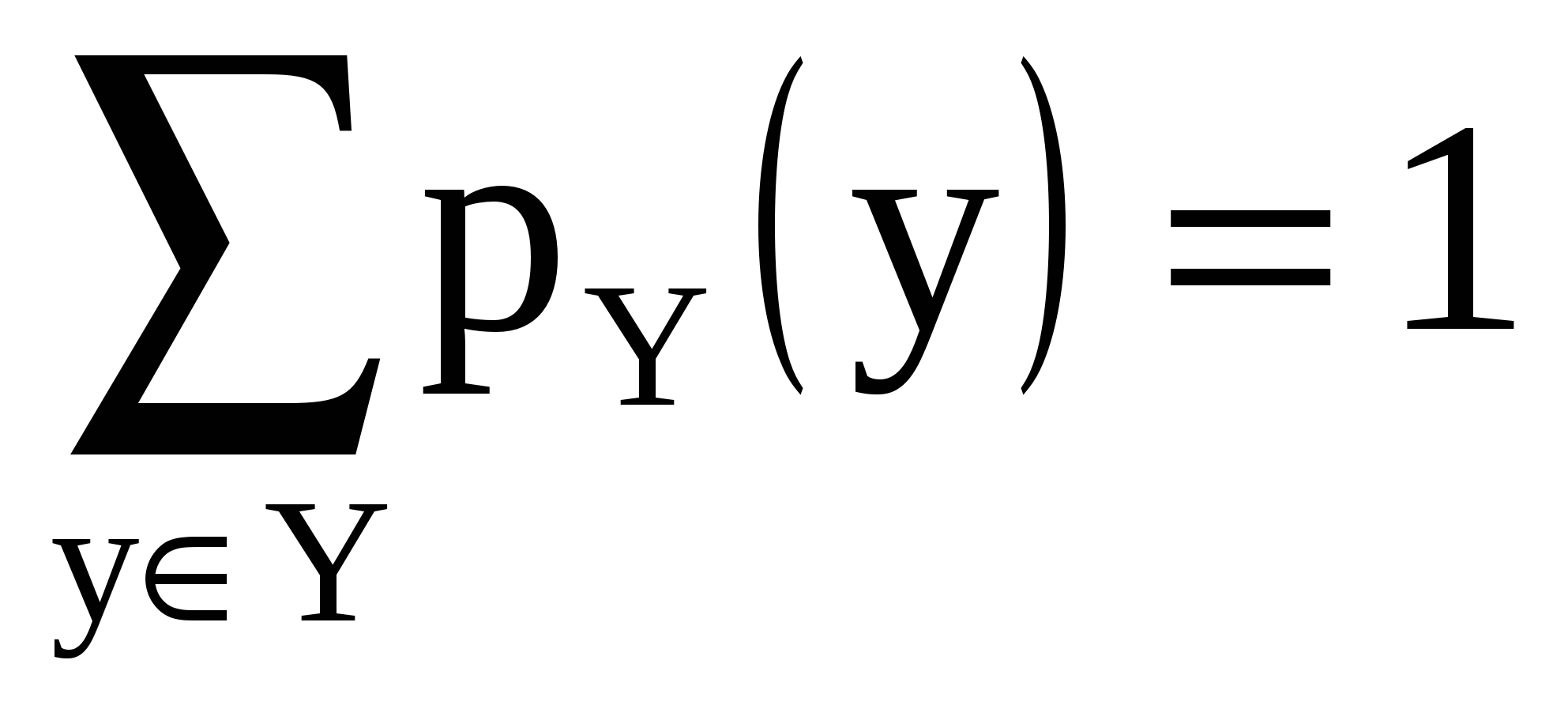
Р  ассмотрим отображение f:X*K Y, определенное условием
ассмотрим отображение f:X*K Y, определенное условием 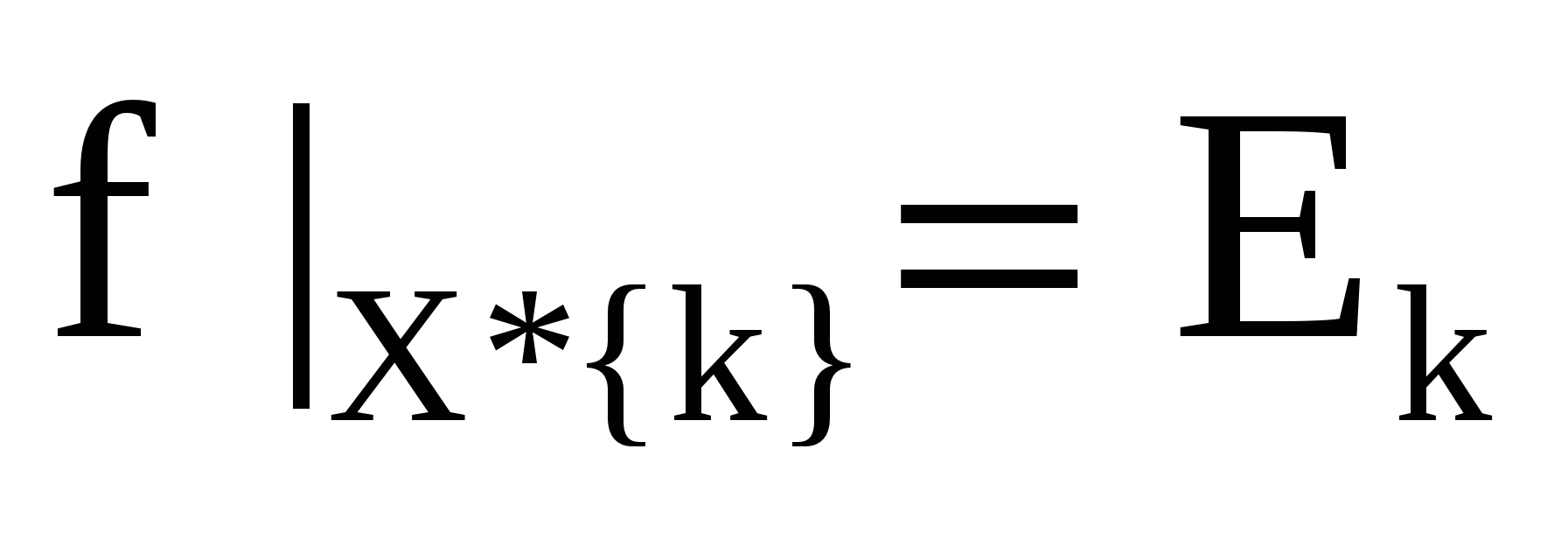 для любого k
для любого k  К . Тогда, поскольку f -1(Y)=X*K , получаем:
К . Тогда, поскольку f -1(Y)=X*K , получаем:  Естественным образом вводятся и условные вероятности Рy/x (y/x), Рy/k (у/k), определяемые формулами
Естественным образом вводятся и условные вероятности Рy/x (y/x), Рy/k (у/k), определяемые формулами
Рy/x (y/x)=  (15)
(15)
РY/K (y/k)= 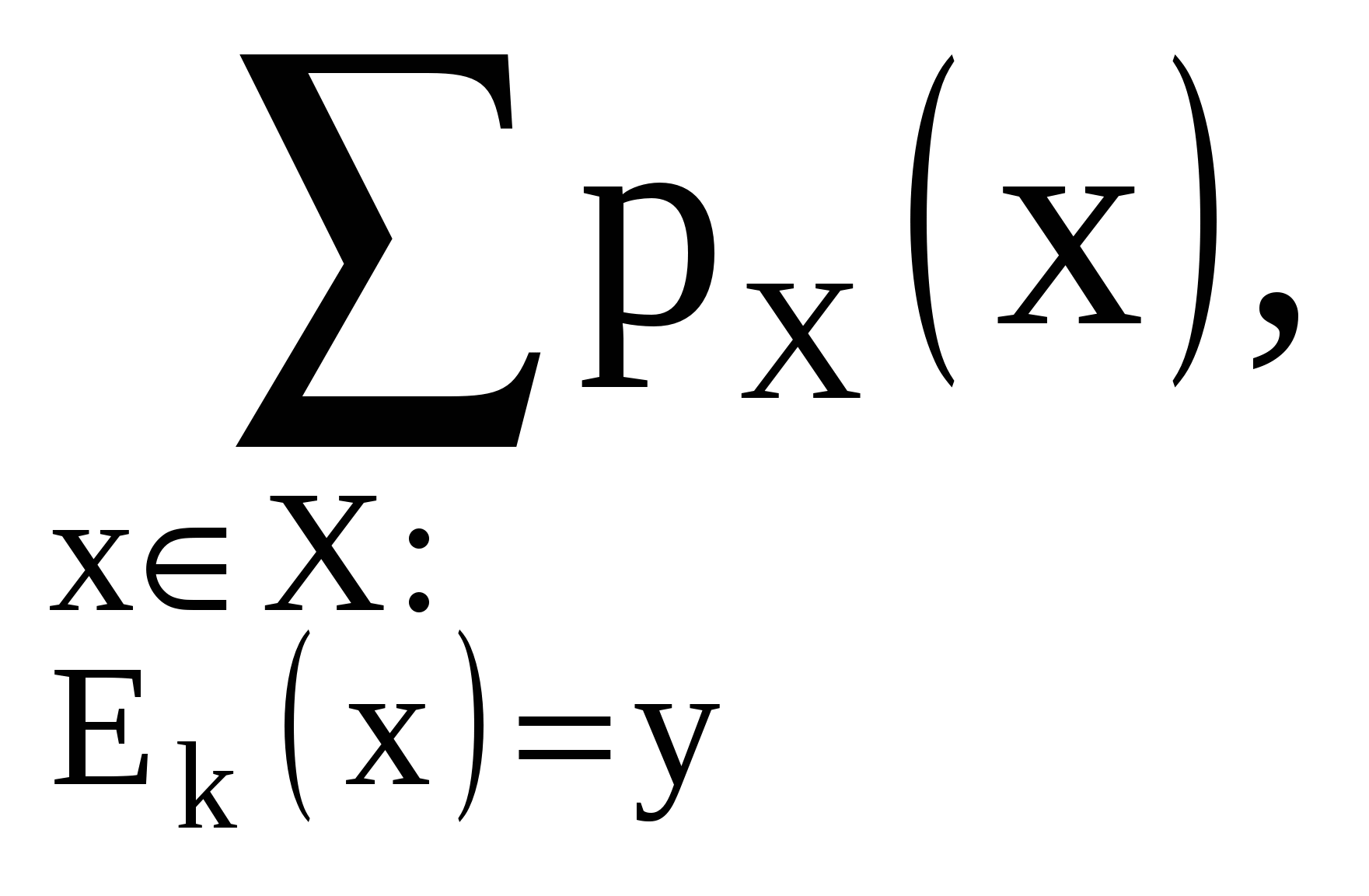 (16)
(16)
Несложно проверить, что формулы (15) и (16) задают вероятностные распределения, то есть что при любом х  Х
Х

и при любом k  К
К
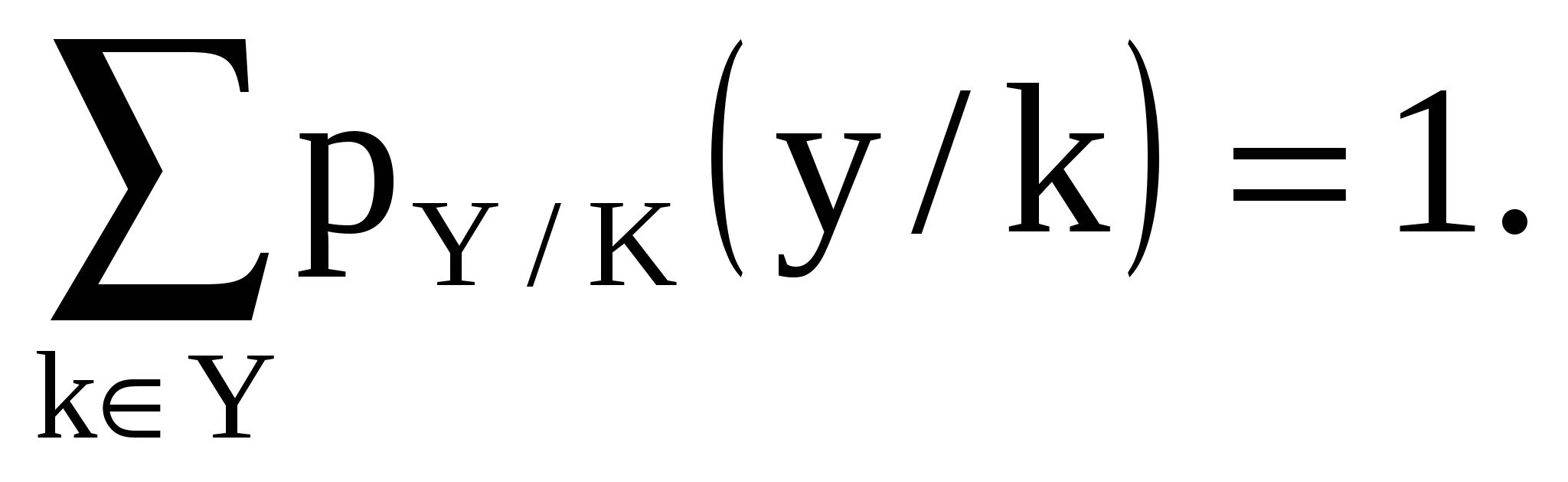
С целью упрощения записи нижние индексы в обозначениях 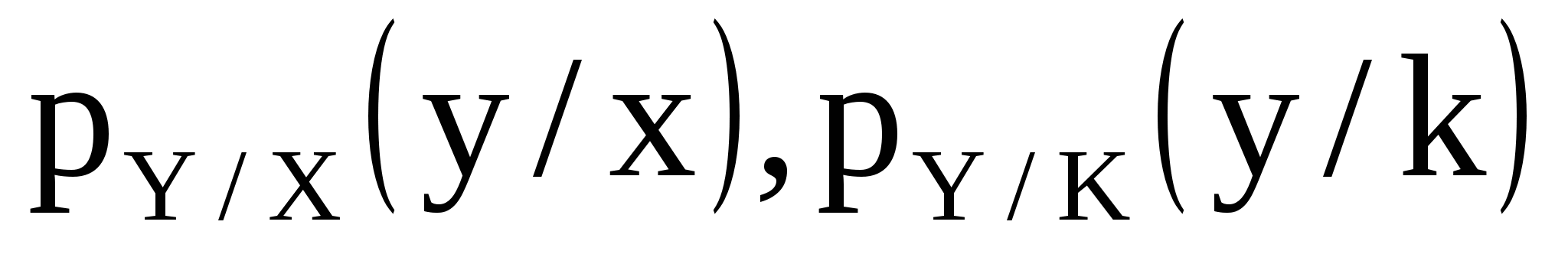 будем опускать, и записывать их в виде р(у/х), p(y/k) соответственно.
будем опускать, и записывать их в виде р(у/х), p(y/k) соответственно.
Отметим, что с помощью формулы для условной вероятности
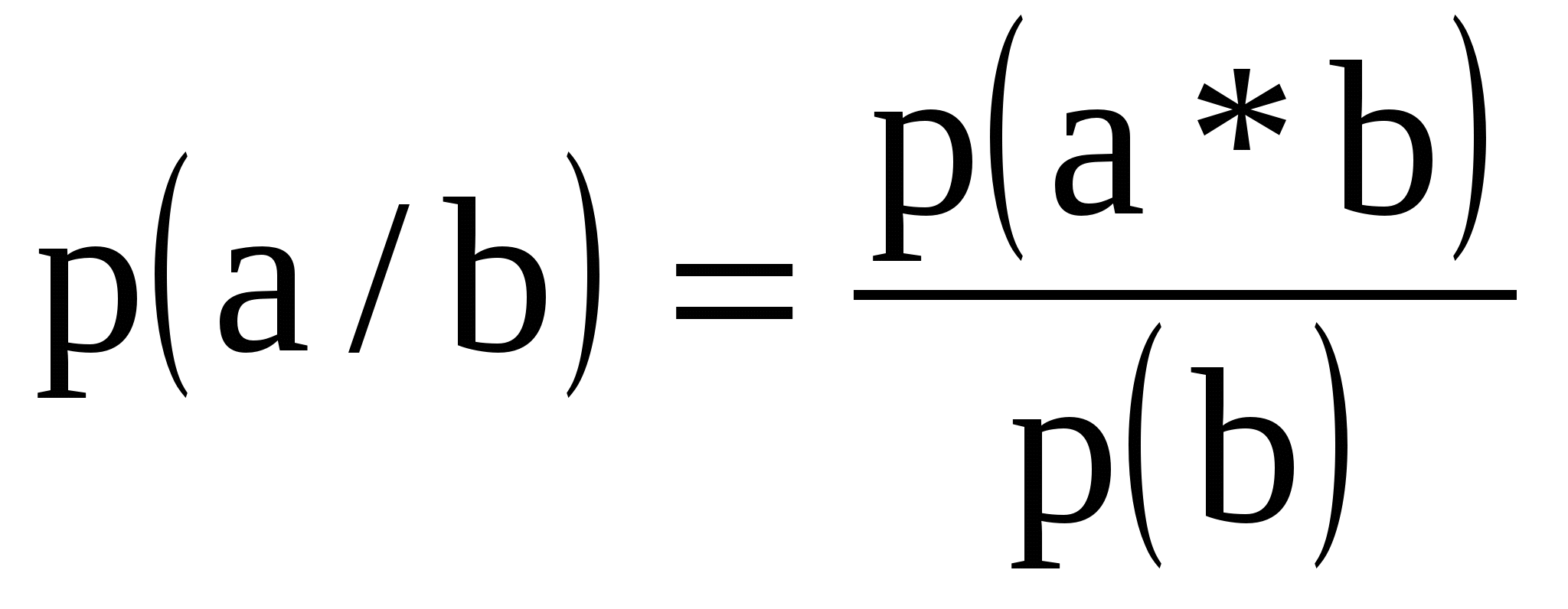 (17)
(17)
мы можем вычислить и условные вероятности p(x/y),p(k/y):
 (18)
(18)
Следующее определение лишь формализует предложенный выше подход к теоретической стойкости шифра (только по отношению к атаке на основе единственного шифртекста).
Определение. Назовем шифр  , совершенным, если для любых x
, совершенным, если для любых x  X,y
X,y  Y выполняется равенство
Y выполняется равенство
Р(х/y)=РX(х). (19)
Отметим одно очевидное свойство совершенного шифра.
Утверждение 1. Если шифр  , — совершенный, то |X|<|Y|<|K|.
, — совершенный, то |X|<|Y|<|K|.
Доказательство. Первое неравенство, очевидно, имеет место для любого шифра. Если шифр — совершенный, то для любых x  X, у
X, у  Y найдется ключ k
Y найдется ключ k  К, такой, что Ek(x)=у . В самом деле, в противном случае, согласно (15), мы бы имели р(у/х)=0, а тогда и (согласно (18)) р(х/у)=0. Согласно (19), вероятность рX(х) также оказывается равной нулю, вопреки нашей договоренности о том, что рX(х) > 0 для любого х
К, такой, что Ek(x)=у . В самом деле, в противном случае, согласно (15), мы бы имели р(у/х)=0, а тогда и (согласно (18)) р(х/у)=0. Согласно (19), вероятность рX(х) также оказывается равной нулю, вопреки нашей договоренности о том, что рX(х) > 0 для любого х  Х .
Х .
Отсюда следует также, что для любого х  Х выполняется равенство {Ek(x),k
Х выполняется равенство {Ek(x),k  K}=Y и, следовательно, |Y| <|К|. Утверждение доказано.
K}=Y и, следовательно, |Y| <|К|. Утверждение доказано.
В большинстве случаев применяемые на практике шифры обладают свойством Х = Y. Следуя К. Шеннону, назовем такие шифры эндоморфными. К. Шеннону удалось полностью описать эндоморфные совершенные шифры с минимально возможным числом ключей. Согласно (20), это минимально возможное число ключей |К| равно |Y|. В несколько более общей форме теорема формулируется следующим образом.
Теорема (К. Шеннон). Пусть  — шифр, для которого |X|=|Y|=|K|. Тогда шифр
— шифр, для которого |X|=|Y|=|K|. Тогда шифр  , — совершенный тогда и только тогда, когда выполняются два условия:
, — совершенный тогда и только тогда, когда выполняются два условия:
1) для любых х  X, у
X, у  Y существует единственный
Y существует единственный
ключ k  К, для которого Еk (х) = у ;
К, для которого Еk (х) = у ;
2) распределение вероятностей Р(К) — равномерное, то есть для любого ключа 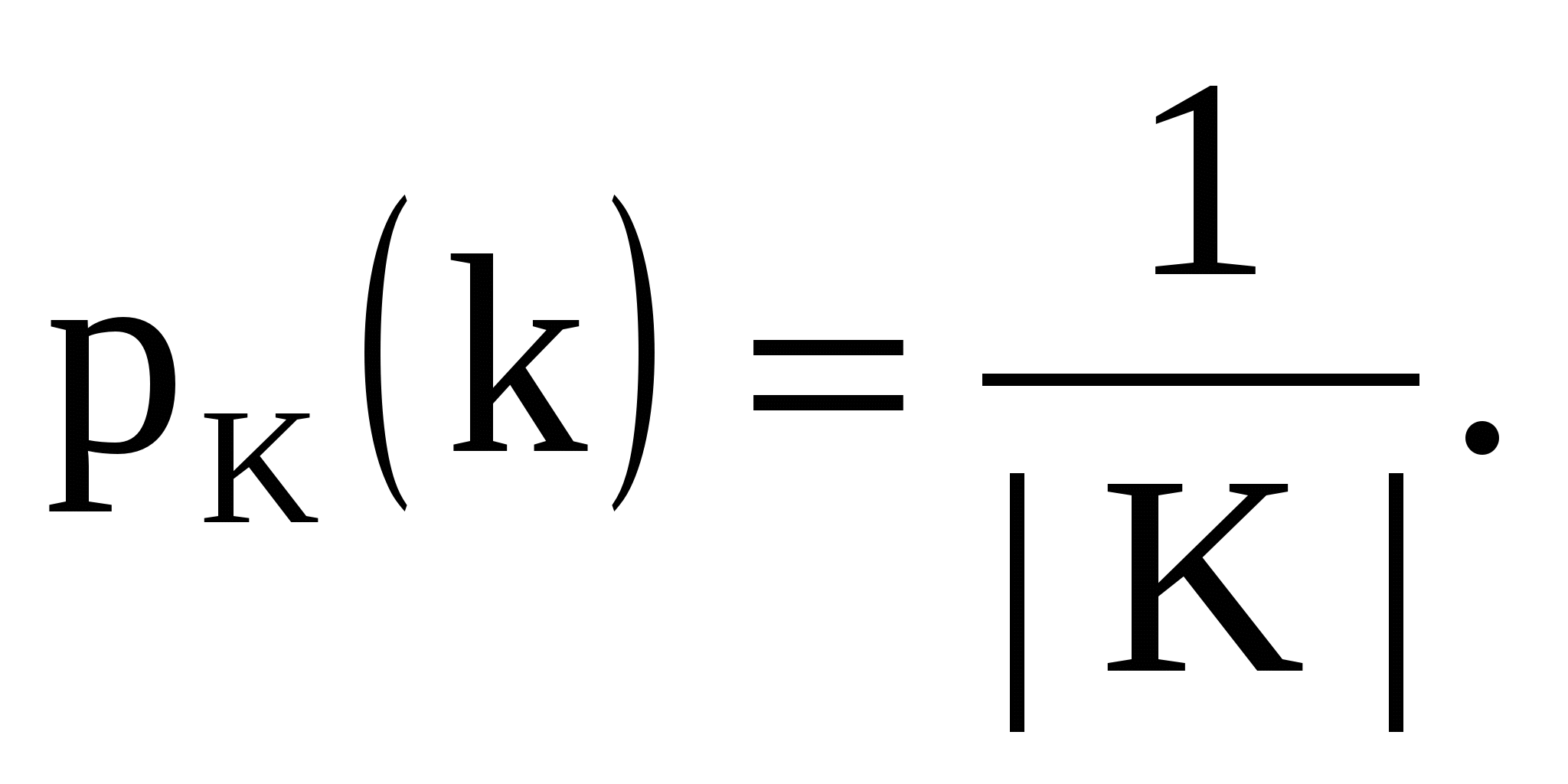
Доказательство. Пусть шифр  — совершенный. Согласно доказательству утверждения 1,
— совершенный. Согласно доказательству утверждения 1,

Поэтому из неравенства  следует неравенств
следует неравенств  для любого х
для любого х  Х . Это доказывает необходимость условия 1).
Х . Это доказывает необходимость условия 1).
Пусть Х = {х1,...,хN}. Зафиксируем произвольный элемент y  Y и занумеруем ключи так, чтобы
Y и занумеруем ключи так, чтобы 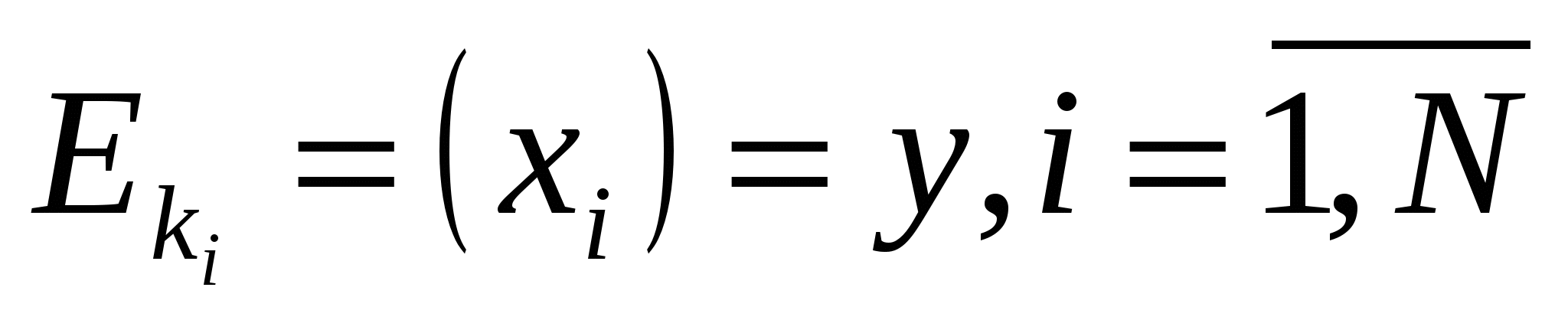 . Тогда
. Тогда
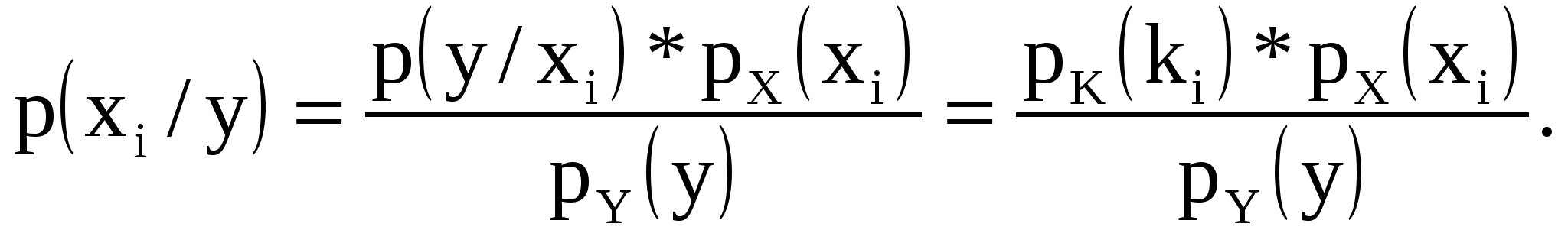 (21)
(21)
Так как  — совершенный шифр, то р(хi/у) = рX (хi). Отсюда и из (21) получаем равенство рK (ki) = рY (у) дл любого i =1,..,N , которое доказывает необходимость условия 2).
— совершенный шифр, то р(хi/у) = рX (хi). Отсюда и из (21) получаем равенство рK (ki) = рY (у) дл любого i =1,..,N , которое доказывает необходимость условия 2).
Пусть условия 1) и 2) выполнены. Тогда, пользуясь для фиксированного элемента у  Y введенной выше нумерацией ключей, имеем цепочку равенств:
Y введенной выше нумерацией ключей, имеем цепочку равенств:

из которой

Достаточность условий теоремы также доказана.
Обратим внимание на то, что таблица зашифрования шифра, удовлетворяющего условиям теоремы Шеннона, согласно условию 1) этой теоремы, является латинским квадратом. Поэтому в случае, когда X=Y=K=Zn сути дела, шифры табличного гаммирования со случайными равновероятными ключами, и только они, являются единственными совершенными шифрами.
| X/K | x1 | … | x1 |
| k1 | 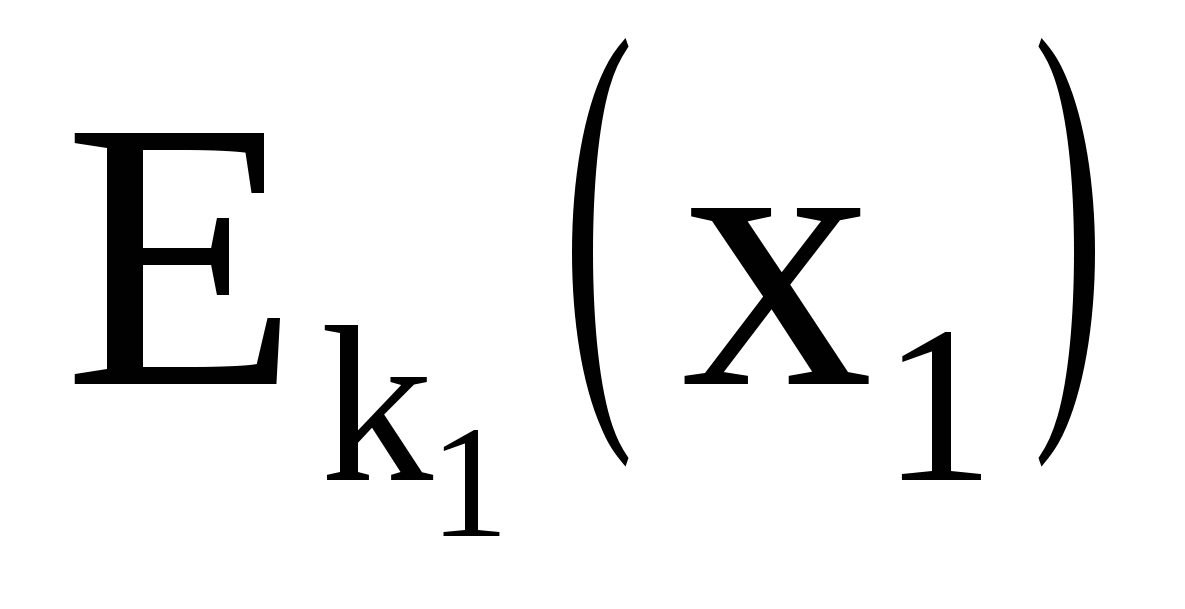
| … | 
|
| … | … | … | … |
| kN | 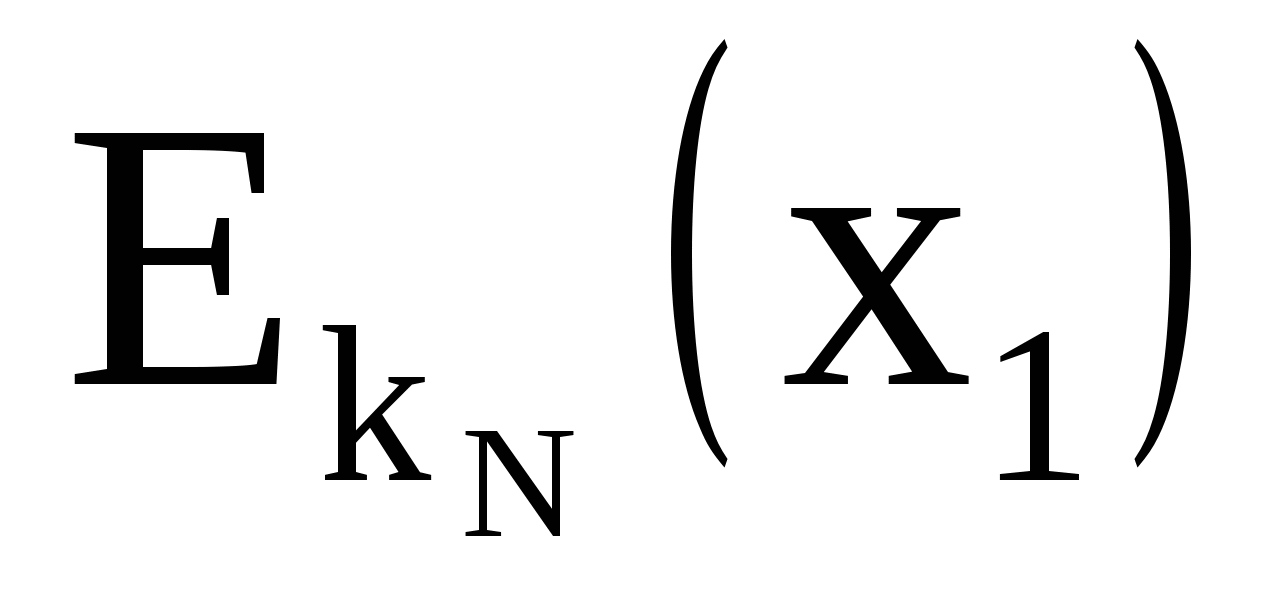
| … | 
|
Легко проверить, что также совершенным будет поточный шифр с основными множествами Х = Y = К =  правилом зашифрования, которое определяется покоординатно как правило зашифрования шифра табличного гаммирования, и равномерным распределением Р(К).
правилом зашифрования, которое определяется покоординатно как правило зашифрования шифра табличного гаммирования, и равномерным распределением Р(К).
Подчеркнем также, что не только указанные шифры являются совершенными. В качестве примера можно указать следующий не эндоморфный совершенный шифр.
Пример
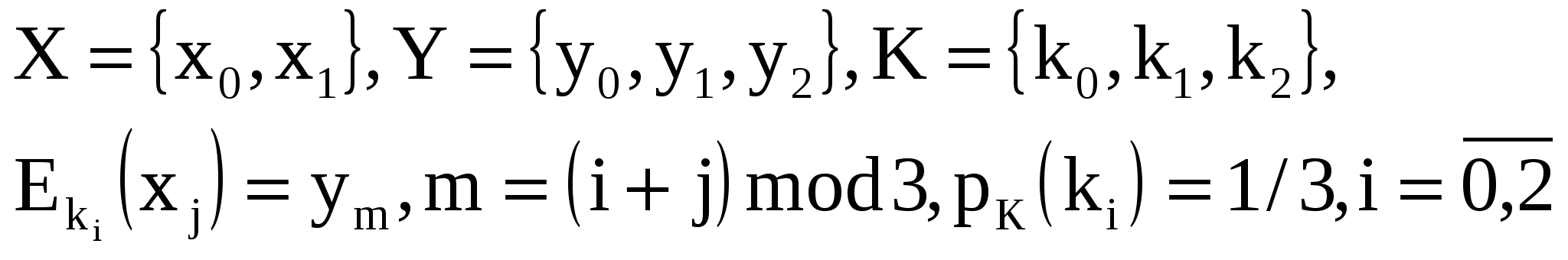
Теорема Шеннона может быть обобщена и для некоторых других криптоатак. Например, в статье [God90] такое обобщение проводится для криптоатак на основе нескольких шифртекстов, полученных на одном ключе, а также для криптоатак на основе ряда открытых и соответствующих им шифрованных текстов, образованных с помощью одного ключа.