Степенная функция, ее свойства и график
Практическая работа
По математике
Тема: «Преобразование графиков функции»
Выполнила: студентка гр. № 6
Вейндель Кэтрин
Содержание:
1. Степенная функция, ее свойства и график;
2. Преобразования
• Параллельный перенос;
• Симметрия относительно осей координат;
• Симметрия относительно начала координат;
• Симметрия относительно прямой y=x;
• Растяжение и сжатие вдоль осей координат.
3. Показательная функция, ее свойства и график, аналогичные преобразования;
4. Логарифмическая функция, ее свойства и график;
5. Тригонометрическая функция, ее свойства и график, аналогичные преобразования (y=sin x; y=cos x; y=tg x);
Функция: y=x\n – ее свойства и график.
Степенная функция, ее свойства и график
y=x, y=x2, y=x3, y=1/x и т. д. Все эти функции являются частными случаями степенной функции, т. е. функции y=xp, где p - заданное действительное число.
Свойства и график степенной функции существенно зависит от свойств степени с действительным показателем, и в частности от того, при каких значениях x и p имеет смысл степень xp. Перейдем к подобному рассмотрению различных случаев в зависимости от
показателя степени p.
- Показатель p=2n -четное натуральное число.
В этом случае степенная функция y=x2n, где n - натуральное число, обладает следующими
свойствами:
- область определения - все действительные числа, т. е. множество R;
- множество значений - неотрицательные числа, т. е. y больше или равно 0;
- функция y=x2n четная, так как x2n=(-x)2n
- функция является убывающей на промежутке x<0 и возрастающей на промежутке x>0.
График функции y=x2n имеет такой же вид, как например график функции y=x4.

2. Показатель p=2n-1- нечетное натуральное число
В этом случае степенная функция y=x2n-1 , где натуральное число, обладает следующими свойствами:
- область определения - множество R;
- множество значений - множество R;
- функция y=x2n-1 нечетная, так как (-x)2n-1=x2n-1;
- функция является возрастающей на всей действительной оси.
График функции y=x2n-1 имеет такой же вид, как, например, график функции y=x3.
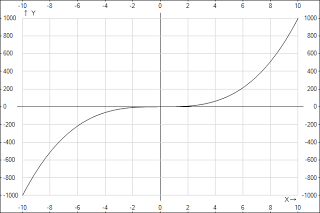
3.Показатель p=-2n, где n - натуральное число.
В этом случае степенная функция y=x-2n=1/x2n обладает следующими свойствами:
- область определения - множество R, кроме x=0;
- множество значений - положительные числа y>0;
- функция y=1/x2n четная, так как 1/(-x)2n=1/x2n;
- функция является возрастающей на промежутке x<0 и убывающей на промежутке x>0.
График функции y=1/x2n имеет такой же вид, как, например, график функции y=1/x2.
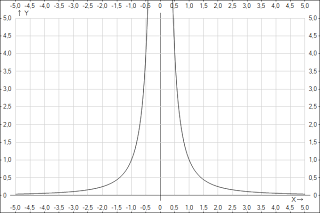
4.Показатель p=-(2n-1), где n - натуральное число.
В этом случае степенная функция y=x-(2n-1) обладает следующими свойствами:
- область определения - множество R, кроме x=0;
- множество значений - множество R, кроме y=0;
- функция y=x-(2n-1) нечетная, так как (-x)-(2n-1) =-x-(2n-1);
- функция является убывающей на промежутках x<0 и x>0.
График функции y=x-(2n-1) имеет такой же вид, как, например, график функции y=1/x3.
