Решение типовых примеров.
(Над знаком = указан номер пункта из теории)
1. 
2. 
3. 
Цель преобразования 
- получить над знаком дифференциала d такое же выражение, как и подынтегральная функция.
Вспомогательные действия
4. 
Проведенная операция 
называется занесением части подынтегральной функции под знак дифференциала. Цель такой операции - получить под знаком дифференциала d такое же выражение, которое стоит в знаменателе подынтегральной функции.
5. 
Для решения этого примера придется использовать формулу интегрирования по частям.
В качестве u выбирают ту часть подынтегральной функции или всю функцию, которая при дифференцировании упрощается. Оставшаяся часть подынтегрального выражения, обязательно содержащая dx, принимается за dv.
Замечание: если в подынтегральную функцию входят arcsin x, arccos x, arctg x, arcctg x, ln x, именно эта функции берутся как u.
6. 
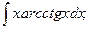
Опять используется формула интегрирования по частям, а т.к. н подынтегральную функцию входит в виде сомножителя arctg x, то u=atcctg x
7. 
В данном примере требуется проинтегрировать дробно-рациональную функцию, которая представлена неправильной рациональной дробью. Первоначально преобразуем подынтегральную функцию. Сделаем это по шагам.
1) Делением уголком выделим у неправильной дроби целую часть и остаток - правильную дробь.
| 2x3 + 5 | x2 – x - 2 | |||||||||
| 2x3 - 2x2 - 4x | 2x + 2 | |||||||||
| 2x2 + 4x + 5 | 
| 2x3 + 5 | = |  2x + 2
Целая часть
| + | 6x + 9 | ||||
| 2x2 - 2x - 4 | x2 – x - 2 |  x2 – x – 2
правильная дробь
| ||||||||
| 6x + 9 |
 |
x2 – x - 2 
= (x - 2)(x + 1)
2) Найдя корни квадратного трехчлена x2 – x – 2
(а проще решив уравнение x2 – x – 2=0 ), сделаем разложение по корням
x2 – x – 2=0, 
x2 – x - 2 = (x - 2)(x + 1)
3) Разложим полученную дробь на сумму простейших дробей с неизвестными (пока) коэффициентами.
| 6x + 9 | = | 6x + 9 | = | A | + | B |
| x2 – x - 2 | (x - 2)(x + 1) | x - 2 | x + 1 | |||
Разложение на сумму простейших дробей
|
4) Найдем неизвестные коэффициенты А и В
| 6x + 9 | = | A | + | B | = | A(x + 1)+В(x - 2) | 
|
| (x - 2)(x + 1) | x - 2 | x + 1 | (x - 2)(x + 1) | ||||
| Одинаковые знаменатели | 
|
6x + 9 = A(x + 1)+В(x - 2)
Применяя в данном равенстве коэффициенты при одинаковых степенях х и, решив систему, найдем А и В.
