Идеальная скорость одноступенчатой ракеты

Определим скорость, которую может получить ракета в идеальном случае, когда ее движение происходит не только за пре­делами атмосферы, но и вне поля тяготения Земли.

В этом случае из выражений (1.4) и (1.8) получаем:

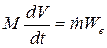
Согласно (1.3)

а тогда

Так как эффективная скорость истечения W_e остается величиной постоянной, после интегрирования получим

где С — произвольная постоянная.

При V = 0 масса ракеты равна начальной массе М₀(суммар­ной массе конструкции, полезного груза и топлива). Поэтому

 

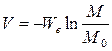
Здесь под M понимается текущее значение массы ракеты, а под V — текущая скорость. Отношение M/M₀обозначается обычно через µ (µ ≤ 1):

По мере выгорания топлива масса М и соответственно вели­чина µ уменьшаются, а скорость V возрастает. Когда двигатель будет выключен, скорость достигнет своего наибольшего конеч­ного значения

(1.12)

 

Здесь под µ_k понимается отношение M_к/M₀, где М_к представ­ляет собой конечную массу, равную стартовой массе ракеты M₀за вычетом массы выгоревшего топлива М_Т. Заметим, что в мо­мент выключения двигателя на дне баков и в трубопроводах еще сохраняются относительно небольшие, меняющиеся от пуска к пуску остатки топлива. Топливо всегда берется с некоторым избытком. Этот номинальный (расчетный) запас топлива назы­вается гарантийным.

Выражение для конечной скорости V_к записывается иногда в виде

Увеличения скорости V_к можно достичь либо повышением эффективной скорости истечения W_e, либо уменьшением относи­тельной конечной массы µ_к. Степень влияния этих параметров на конечную скорость не одинакова. Если продифференцировать выражение (1.12) и заменить дифференциалы конечными при­ращениями, то получим

Отсюда можно заключить, что сравнительно большее влия­ние на идеальную скорость V_к оказывает эффективная скорость истечения W_e, если только

,

т. е. если

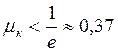
Для всех одноступенчатых баллистических ракет это условие

 

выполняется. Таким образом, наиболее сильно влияет на иде­альную скорость эффективная скорость истечения, а соответ­ственно и удельная тяга двигателя. Но этим, однако, не сни­жается роль весовой характеристики µ_к. Все равно, чем меньше µ_к, тем большую скорость может получить ракета при той же удельной тяге. А уменьшить µ_кпри заданном полезном грузе можно, только уменьшая вес самой конструкции.

Для оценки весового качества конструкции применяются раз­личные показатели. Одним из весьма распространенных яв­ляется безразмерный коэффициент весового качества, опреде­ляемый отношением

где µ_п.г. — относительная масса или относительный вес полезного груза,

Представление о реальных значениях α_к можно получить, если вспомнить, например, что стартовый вес первой немецкой баллистической ракеты «Фау-2» составлял примерно 13 тс при собственном весе конструкции (без боевого заряда), равном 3 тс. Боевой заряд имел вес около одной тонны. Таким образом, после элементарных подсчетов получаем для этой ракеты µ_к = 0,3 и α_к = 0,25.

Понятно, что конструкция этой ракеты по нынешним пред­ставлениям весьма несовершенна, поэтому полученное значение α_к следует рассматривать сейчас как некоторый нижний, легко достижимый показатель весового качества. Для современных ра­кет-носителей величина α_к достигает значений 0,06—0,08 в зави­симости от плотности применяемого топлива, а величина 0,05 рассматривается в настоящее время как верхний, практически недостижимый предел. Что же касается относительного конеч­ного веса µ_к, то он определяется в первую очередь величиной полезного груза и для существующих одноступенчатых ракет может меняться в диапазоне 0,15—0,35.

Идеальная скорость V_k (1.12) представляет собой верхний предел достижимой скорости в идеальных условиях. В реальных условиях полета неизбежны потери скорости вследствие земного тяготения, аэродинамического сопротивления и некоторых дру­гих причин, о которых будет сказано позже. Сумма этих потерь может быть приближенно оценена заранее. Поэтому для каждой технической задачи, решение которой преследуется создаваемой ракетой, можно и заранее с достаточной точностью указать идеальную скорость, которая должна быть обеспечена надлежа­щим выбором параметров ракеты. Такая скорость называется характеристической и обозначается через V_x. Это — идеальная скорость, которой должна обладать ракета, спроектированная для решения конкретной баллистической задачи. Так, например, для пуска ракеты с околоземной орбиты к Луне необходимо рас­полагать характеристической скоростью V_x = 3200 м/сек. Для выведения спутника с поверхности Земли на низкую орбиту нужна характеристическая скорость около 9400 м/сек (фактиче­ская скорость 7500 м/сек). Точное же значение V_x становится из­вестным лишь после того, как ракета спроектирована.

Если эффективную скорость истечения W_e довести до 4400 м/сек. что приближается к границе энергетических возмож­ностей химических ракетных топлив, и при этом одновременно до реального предела уменьшить µ_k, скажем — до 0,12, то тогда согласно (1.12) получим

что меньше характеристической скорости, необходимой для вы­хода на околоземную орбиту. Таким образом, путем элементар­ных числовых выкладок мы приходим к вы­воду, что достижение первой космической скорости для создания искусственного спутника Земли находится на пределе реальных возможностей одноступенчатых ракет с двигателем на химическом топливе. Такие одноступенчатые ракеты-носители пока не созданы, но не исключена возможность их появления в не столь отдаленном будущем.

Итак, скорость в идеальных условиях полета определяется параметрами W_e и µ_к. Посмотрим теперь, от каких параметров зависит путь s_к, пройденный ракетой в идеальных условиях за время t_к.

Очевидно

При условии неизменного расхода текущая масса линейно зависит от времени:

Поэтому

(1.14)

и тогда

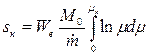
или

Так как

то

и поэтому

 

где под v₀ понимается отношение стартового веса к стартовой тяге. Эту величину называют стартовой нагрузкой на тягу

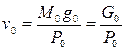(1.15)

где P₀ - тяга, равная в идеальных условиях пустотной, а G₀ – стартовый вес ракеты, соответствующий земным условиям.

Величину, обратную стартовой нагрузке на тягу

иногда называют тяговооруженностъю — термин, перекочевав­ший в свое время в ракетную технику из военного лексикона. Независимо от того, пользуемся ли мы параметром v₀ или n₀, необходимо подчеркнуть главное. Если скорость ракеты в усло­виях идеального движения определяется двумя параметрами, то путь определяется тремя и зависит не только от W_e и µ_к, но и от тяговооруженности или, иначе говоря,— от стартового ускорения.