Пример отыскания условного экстремума

Решим задачу:

Найти экстремумы функции при условии .

Дадим два решения этой задачи.

Первое решение основано на том, что уравнение связи можно в явном виде решить: и получить, подставив эти значения в функцию , соответственно, две непрерывные функции от : , .

Для решения поставленной задачи следует найти экстремумы этих функций. Первая из них имеет максимум в точке , вторая – минимум в точке .(Проверьте это самостоятельно).

Недостатком предложенного выше способа является то, что мы использовали явный вид решения уравнения связи. Во многих случаях решить уравнения связи непросто. Поэтому рассмотрим второе решение, которое использует изложенный выше метод Лагранжа.

Строим функцию Лагранжа . Составим и решим соответствующую систему уравнений

При получаем При

Функция может иметь условный экстремум только в этих точках.

Выясним, действительно ли в этих точках есть экстремумы.

С этой целью найдем .

Вторые частные производные равны .

Из условия следует , и в точке , т.е. . В точке , т.е. снова . Поэтому .

В точке второй дифференциал равен , т.е. в этой точке имеем условный максимум, а в точке – второй дифференциал равен , т.е. в этой точке имеем условный минимум.

Для иллюстрации теории, описанной в предыдущем пункте, рассмотрим окаймлённый гессиан

,

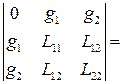
последнее равенство получено, как следствие уравнения связи. При в соответствующей точке имеем минимум, так как окаймлённый гессиан отрицателен( равен ). При в точке имеем максимум, так как окаймлённый гессиан положителен( равен ).

 

Приложения теории условного экстремума к экономической теории