Составляющие прямой обратной и нулевой последовательности ЭДС обмоток трансформатора.

Сопротивления симметричной трехфазной цепи для токов различных последовательностей

Если к выводам симметричной трехфазной цепи приложена симметричная система напряжений прямой, обратной или нулевой последовательностей, то в цепи возникает симметричная система токов соответственно той же самой последовательности, какую имеют приложенные напряжения. Отношения приложенных комплексных фазных напряжений прямой, обратной и нулевой последовательностей к соответствующим комплексным фазным токам называют соответственно комплексными сопротивлениями цепи прямой (Z1, обратной (Z2) и нулевой (Z0) последовательностей.

В любых симметричных трехфазных статических цепях (цепях, не содержащих вращающихся машин) изменение порядка следования фаз приложенных симметричных напряжений с прямого на обратный не изменяет значения токов (изменяется только их последовательность с прямой на обратную). Поэтому для таких цепей сопротивления прямой и обратной последовательностей одинаковы (Z1 = Z2).

Рассмотрим, например, трехфазную симметричную цепь (рис. 11.7), в которой Z_A =Z_B=Z_C=Z.

Очевидно, что для этой цепи Z₁=Z₂=Z.

Определим для нее Z₀.

Пусть к выводам цепи приложена симметричная система фазных напряжений нулевой последовательности U_A=U_B=U_C=U₀. при этом система токов также симметрична и имеет нулевую последовательность I_A=I_B=I_C=I₀. Ток в нейтральном проводе I_N=3I₀.

Составим для контура AnNA уравнение

и, подставив и Z_A=Z, получим U₀=(Z+3Z_N)I₀, откуда

При отсутствии нейтрального провода токи нулевой последовательности протекать не могут: Z₀=∞ и I₀=0.

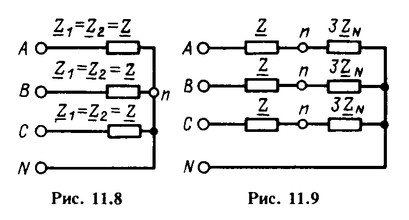При расчетах цепей методом симметричных составляющих рассматривают отдельно схемы для токов и напряжений различных последовательностей. Сопротивление в нейтральном проводе не оказывает влияния на симметричные системы токов прямой и обратной последовательностей, поэтому в схемах для токов этих последовательностей сопротивления в нейтральном проводе не указывают (рис. 11.8). В схеме для симметричных токов и напряжений нулевой последовательности вместо сопротивления Z_N в нейтральном проводе вводят утроенные значения этого сопротивления в каждую фазу (рис. 11.9). Легко проверить, что сопротивления нулевой последовательности для схем, представленных на рис. 11.7 и 11.9, одинаковы.

Все расчеты ведут для одной фазы, которую называют основной. Обычно за основную фазу принимают фазу А, и в этом случае для сокращения записи в обозначениях токов и напряжений различных последовательностей индекс А не пишут. Так, для рассматриваемого примера (см. рис. 11.7) на рис. 11.10 показаны три однофазные схемы для токов и напряжений различных последовательностей. Эти схемы сокращенно называются схемами прямой, обратной и нулевой последовательностей.

В качестве схем прямой и обратной последовательностей для трехфазных линий можно применять любую из двух схем, показанных на рис. 30 и 31. В схему нулевой последовательности должны быть введены утроенные значения сопротивления г, и индуктивности М (см. рис. 29) в каждую фазу. В зависимости от того, разнесены частичные емкости поровну по концам линии или сосредоточены в середине, получатся две разновидности схем нулевой последовательности для трехфазной линии, не отличающиеся по структуре от схем, показанных на рис. 30 и 31. Только в этих схемах вместо r, L_ф, C_ф следует взять r₀=r+3r₃, L₀=L_ф+3M=L+2M и С₀ (через частичные емкости С_m токи нулевой последовательности протекать не могут).