Т е о р и я м е т о д а
Всякий, даже “мгновенный” процесс на самом деле длится некоторое время, хотя быть может и очень короткое. Изучение переходных процессов, т.е. установление того или иного явления стационарного течения процессов, позволяет часто глубже вскрыть природу и ход самого явления, понять его, а следовательно и использовать на практике. В области электрических явлений особый интерес представляют переходные процессы при заряде и разряде конденсатора.
Зарядка конденсатора начинается с момента присоединения конденсатора к источнику постоянного тока (схема 1) и длится до момента полного заряда конденсатора т.е. до возникновения разности потенциалов на пластинах конденсатора равной э.д.с. источника. При этом, очевидно, на конденсаторе появится напряжение U, направленное противоположно э.д.с. источника e1. Рост напряжения на конденсаторе по мере накопления зарядов на его обкладках вызывает уменьшение зарядного тока, определяемого формулой 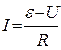
т.к. действующее значение напряжения, равное в каждый момент разности e- U убывает.
 В момент полного заряда конден-
В момент полного заряда конден-
сатора, 
 когда U станет равным e,
когда U станет равным e,
действующее напряжение окажется
равным нулю и тогда ток заряда
прекратится. Теоретически это
наступит через бесконечно боль-
Схема I. шое время, а практически, если конденсатор заряжается через малое сопротивление, почти мгновенно. Такое убывание тока от максимального до нуля наблюдается при разряде конденсатора, так как ток пропорционален изменению заряда в единицу времени  (1), величина заряда пропорциональна емкости конденсатора dq =с dU, то
(1), величина заряда пропорциональна емкости конденсатора dq =с dU, то  (2)
(2)
По закону Ома  (3)
(3)
Тогда из уравнений (2) и (3) получим
 или
или  (4)
(4)
Формула (4) показывает, что относительный спад напряжения на конденсаторе  пропорционален протекшему времени и обратно пропорционален произведению R× с. Следовательно, спад напряжения на конденсаторе происходит тем медленнее, чем больше R и чем больше с, составляющие разрядную цепь. Важным параметром, характеризующим цепь из последовательно соединенных сопротивлений и емкости, является произведение R× с, которое называется постоянной времени цепи. Если взять интегралы от обеих частей уравнения
пропорционален протекшему времени и обратно пропорционален произведению R× с. Следовательно, спад напряжения на конденсаторе происходит тем медленнее, чем больше R и чем больше с, составляющие разрядную цепь. Важным параметром, характеризующим цепь из последовательно соединенных сопротивлений и емкости, является произведение R× с, которое называется постоянной времени цепи. Если взять интегралы от обеих частей уравнения

 (5)
(5)
знак «минус» указывает на убыль напряжения, то можно определить закон изменения тока при разряде конденсатора



 ;
;

 ;
;
С учетом того, что e = I0R, I = 
имеем I= 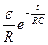 =I
=I 




где I - сила тока к моменту времени, Iо - максимальная сила тока при R - сопротивление, с - емкость, t - время, е - основание натурального логарифма.
Обозначим Rс =  - постоянная времени цепи. Если
- постоянная времени цепи. Если  = t, то
= t, то
I=I 
 =
=  = 0,37 I
= 0,37 I 
Постоянная времени цепи показывает, что через Rс секунд сила тока убывает в 2,7 раза, или составляет от максимального значения 0,37Iо (рис. 1).
 В задачу настоящей работы входит:
В задачу настоящей работы входит:
изменение силы разрядного тока через различные промежутки времени.
Определение по этой кривой постоянной времени и сравнение t
полученной величины с результатом
расчета по формуле  = Rс
= Rс
рис.1