Фурье-преобразование сигнала
В области спектрального (или гармонического) анализа используются прямое и обратное дискретное преобразование Фурье, а также вариант его рационального вычисления – быстрое преобразование Фурье:
где 
. Трудоемкость вычисления составляет порядка N2 комплексных умножений и столько же комплексных сложений.
Выполним некоторые преобразования:
= 
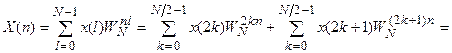
Таким образом, вычисление N-точечного преобразования можно произвести путем вычисления двух N/2-точечных: B(k), k=0,2,4,6,…,N-1 и C(k), k=1,3,5,…,N-1.
Учитывая, что преобразование Фурье длиной N/2 элементов периодично с периодом N/2 точек, т.е. B(n) = B(n + N/2) и С(n) = С(n + N/2), получаем
, поскольку 
.
Таким образом
Трудоемкость вычислений преобразования теперь составит порядка 
комплексных умножений и в 2 раза больше комплексных сложений. Вычисление коэффициентов Wn осуществляется либо с использованием подпрограмм вычисления синуса и косинуса, либо табличным способом (чаще всего), либо каким-нибудь другим способом.
Аналогично, два N/2-точечных преобразования можно свести к четырем N/4-точечным и так далее. При этом сокращение объема вычислений составит (при N равном степени числа 2):
.
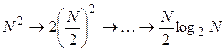Порядок адресации элементов при выполнении, например, четырех 2-х точечных преобразования (при N=8) будет такой:
Представим адреса элементов в двоичном коде и переставим биты в обратном (реверсном) порядке:
| Прямой: | ||||||||
| Реверсный: | ||||||||
| Значение: |
Как видно из этого примера для эффективной реализации преобразования Фурье необходима аппаратная поддержка бит-реверсного режима адресации данных и возможности выполнения дуального сложения/вычитания..