Арифметические операции над числами с плавающей запятой.

1.Алгоритм сложения и вычитания.

Дано: x = S_xM_xp^q_x

y = S_yM_yp^q_y

Найти: z = x 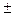y = S_zM_zp^q_z

1) Находим максимальный порядок из 2-х слагаемых: q’_z = max(q_x, q_y).

2) Если порядок ч больше или равен порядку у (q_x 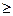q_y), тогда определяем промежуточную мантису у: M’_y = M_yp^q_y^-q_x;

M’_x = M_x.

Если q_у 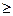q_х, тогда: M’_x = M_xp^q_x^-q_y;

M’_y = M_y.

3) Определяем предварительный результат:

z’ = S_zM’_zp^q_z;

S_zM’_z = S_xM’_x 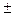S_yM’_y.

Если число нормализованное, то z = z’, если число не нормализованное, тогда выполняем нормализацию по следующему алгоритму:

z = H(z’)

а) Если M’_z < 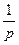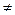0, то ищем смещение - округление в меньшую сторону, тогда M_z = M’zp^Δ,

q_z = q’_z – Δ.

б) Если М’_z > 1, тогда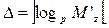

M_z = M’zp^-Δ,

q_z = q’_z + Δ.

2. Операция умножения.

Определить z = x*y = S_zM_zp^q_z

1) S_z = S_x +S_y

2) Предварительная мантиса M’_z = M’_x * M’_y.

3) Предварительный порядок q’_z = q_x + q_y.

4) Предварительное число z’ = S_zM’_zp^q’_z.

5) z = H(z’)

3. Операция деления.

Определить z = x/y = S_zM_zp^q_z

1) Sz = Sx +Sy

2) Предварительная мантиса M’_z = M’_x / M’_y.

3) Предварительный порядок q’_z = q_x – q_y.

4) Предварительное число z’ = S_zM’_zp^q’_z.

5) z = H(z’)

 

Пример: x = 0.51*10⁵

y = -0,52*10⁵

S_x = + S_y = –

Mx = 0.51 S_y = 0.52

p = 10 p = 10

q = 5 q = 5

1) q = 5

2) M’x = 0.51 M’y = 0.52

3) S’zM’z = 0.51 – 0.52 = -0.01

z’ = -0.01*10⁵

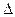= -[[log₁₀0.01]+1] = -[-1] = 1

q_z = 5-1 = 4

M_z = 0.01*10¹ = 0.1

z = -0.1*10⁴

Операция умножения:

M’_z = 0.51*0.52 = 0.2652

q’_z = 10

z’ = -0.2652*10⁴

 

Если производятся операции с двоичными числами, то необходимо в результирующем числе использовать смещенный порядок, который определяется как:

,

где М^* - максимальный размер разрядной сетки.

Если число М^* разрядное - М^* = 16, М^*/2 = 8, то к каждому порядку нужно добавлять 8, в двоичном коде 1000, при действиях с двоичными числами операции проводятся отдельно над мантисами, отдельно над порядками. Хранятся мантисы и порядки в разных местах.

120₁₀

q = 7₁₀ 0111

q = ]log₂ 120[ = 7

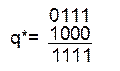
q* = 1111

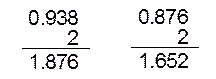
S 0

q* 1111

M 0.11100

 

Основные операции над логическими переменными и основные логические функции.

Все переменные и функции от них, которые могут принимать только два значения – 0 и 1, называются логическими или булевыми функциями. Исследованиями свойств логических функций занимается математическая логика (двоичная алгебра).